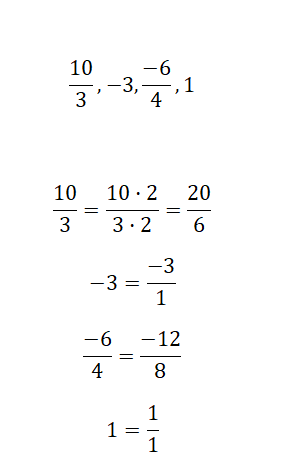En este artículo encontrarás una explicación sobre las fracciones equivalentes o fracciones iguales muy completa y fácil de entender. Concretamente, hablaremos sobre su definición, cómo calcularlas y cómo saber si dos fracciones son equivalentes. De esta manera, acabarás sabiendo todo lo necesario para resolver ejercicios de fracciones equivalentes como los que te plantearemos al final. Dicho esto, empezamos con el temario.
Contenido
Calculadora de fracciones equivalentes
Con la ayuda de esta calculadora de fracciones equivalentes podrás comprobar si dos fracciones son iguales, sin la necesidad de hacer cálculos. Su funcionamiento es muy simple, básicamente tienes que introducir los valores correspondientes a los dos numeradores y a los dos denominadores y darle en el botón de «Calcular».
¿Qué son las fracciones equivalentes?
Las fracciones equivalentes son aquellas que expresan un mismo valor numérico, por lo tanto, son fracciones que equivalen a un mismo resultado, aunque tengan un numerador y un denominador distintos. Esto quiere decir que mantienen una relación de proporcionalidad, la cual puede ser de dos tipos: amplificada o simplificada. A continuación, te mostramos un ejemplo gráfico de fracciones equivalentes para que se entienda mejor el concepto.

En la anterior imagen se pueden ver dos círculos divididos en dos y cuatro partes. Si tratamos de definir el primero a través de una fracción diremos que cada parte equivale a 1/2 del total, mientras que en la segunda figura usaremos la fracción 1/4. Evidentemente, estas dos fracciones no son equivalentes, ya que representan cantidades diferentes. Pero, si cogemos dos trozos del segundo círculo (2/4), esta expresión sí que equivale a 1/2.

En esta segunda imagen se puede ver la equivalencia entre 1/2 y 2/4, además, se puede comprobar numéricamente. Ya que 1/2 = 0,5 y 2/4 = 0,5. Según la definición que hemos comentado previamente, si las dos fracciones expresan un mismo valor numérico, entonces son fracciones equivalentes.
Ejemplos de fracciones equivalentes
Ahora te mostraremos 5 ejemplos de fracciones equivalentes. Y si quieres entender cómo las hemos calculado, te recomendamos que sigas leyendo.
- Fracciones equivalentes a un medio: 2/4, 3/6, 4/8, etc.
- Fracciones equivalentes a un tercio: 2/6, 3/9, 4/12, etc.
- Fracciones equivalentes a un cuarto: 2/8, 3/12, 4/16, etc.
- Fracciones iguales a la unidad: 4/4, 7/7, 15/15, etc.
- Fracciones equivalentes a un quinto: 2/10, 3/15, 4/20, etc.
¿Cómo calcular fracciones equivalentes?
Para obtener fracciones equivalentes tenemos que multiplicar o dividir tanto el numerador como el denominador, por un mismo número. Ya que, si modificamos de igual forma ambas partes de la fracción, mantenemos una relación de proporcionalidad. Por lo tanto, podremos usar dos métodos: amplificación y reducción.
Hallar una fracción equivalente por amplificación
En este primer caso, tenemos que multiplicar una fracción inicial por un determinado valor numérico. Esto quiere decir que tenemos que multiplicar el numerador y el denominador por ese número. Para que lo veas con un ejemplo, a continuación te mostramos dos fracciones equivalentes, que se obtienen después de hacer una multiplicación:

Lo que hemos hecho ha sido multiplicar ambas partes de la fracción por tres: 5 x 3 = 15 y 4 x 3 = 12. Obteniendo así una fracción equivalente amplificada, ya que es más grande. En conclusión, hemos hallado una fracción compuesta por diferentes valores numéricos, la cual expresa una misma cantidad que la fracción original.
Hallar una fracción equivalente por simplificación
En segundo lugar, podemos optar por simplificar una fracción, dividiendo el numerador y el denominador de una determinada fracción. De esta manera, conseguiremos otra fracción equivalente, aún más sencilla que la inicial. Aunque, cabe mencionar que este método solo funciona si la expresión inicial no es una fracción irreducible, ya que, estas últimas no se pueden reducir más. A continuación puedes encontrar un ejemplo de cálculo de una fracción equivalente por reducción (simplificación).

Como se puede ver en la imagen, lo que hemos hecho ha sido dividir tanto el numerador como el denominador de la fracción entre un divisor común. En este ejemplo, hemos usado el cinco: 25 / 5 = 5 y 15 / 5 = 3. Finalmente, hemos obtenido la fracción equivalente irreducible de 25/15.
¿Cómo saber si dos fracciones son equivalentes?
Para identificar fracciones equivalentes tenemos que seguir alguno de los tres procedimientos que explicaremos a continuación. Cabe destacar que el segundo está relacionado con la simplificación de fracciones que hemos comentado en el anterior apartado.
Multiplicación de numeradores por denominadores
Si quieres comprobar la equivalencia que hay entre dos fracciones puedes utilizar este primer procedimiento. Básicamente, tienes que multiplicar el numerador de la primera fracción por el denominador de la segunda. Después, tienes que multiplicar el numerador de la segunda fracción por el denominador de la primera. Si los dos resultados te dan lo mismo, entonces esas fracciones serán equivalentes. Observa el ejemplo siguiente:

En este último ejemplo, hemos comprobado que las dos fracciones eran equivalentes. Este ejemplo era fácil de ver, ya que la segunda fracción es el doble de la primera, dicho de otro modo, guardan una relación de equivalencia amplificada. Cabe destacar que este procedimiento es bastante cómodo de usar, simplemente hace falta multiplicar en cruz. Pero igualmente te recomendamos que aprendas a utilizar los otros dos sistemas, porque así tendrás más recursos matemáticos a tu disposición.
Simplificación de fracciones
Cuando estamos tratando con fracciones no irreducibles podemos usar este otro método, el cual consiste en reducir al máximo la fracción que esté compuesta por los números más grandes. Si al hacer esta reducción, nos encontramos con que la fracción más pequeña es la irreducible de la otra, entonces podemos dar por sentado que son equivalentes.

Resolver e igualar las divisiones
Por último, puedes recurrir a la solución del cociente que generan las fracciones, porque un número fraccionario no deja de ser una división. Básicamente, tienes que calcular el valor numérico equivalente a ambas fracciones, y si se trata del mismo número, entonces serán equivalentes. En la siguiente imagen puedes ver un ejemplo muy claro:

Ejercicios de fracciones equivalentes
Ahora que ya has leído toda la teoría puedes probar de resolver los siguientes ejercicios, los cuales te permitirán acabar de entender la explicación. Te recomendamos que trates de resolverlos por tu cuenta y una vez los tengas, compares tu resultado con el que te ofrecemos nosotros. Dicho esto, te dejamos practicar:
Ejercicio 1
Encuentra una fracción equivalente por simplificación para cada fracción que te proponemos:
Para resolver este ejercicio solamente hay que aplicar la simplificación de fracciones, de esta manera obtenemos la fracción irreducible equivalente. Los cuatro ejemplos son muy similares, por lo tanto, no hay mucha dificultad de resolución.
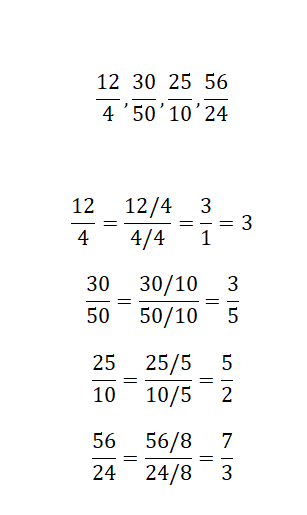
Ejercicio 2
Encuentra una fracción equivalente por amplificación para cada fracción que te proponemos:
A continuación tendrás que amplificar las fracciones que te proponemos, de esta manera, obtendrás fracciones equivalentes más grandes. No importa el número que uses para hacer las multiplicaciones, nosotros por ejemplo lo haremos con 2 y 3.
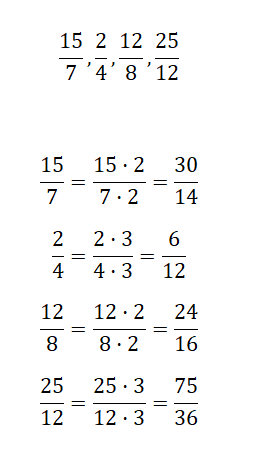
Ejercicio 3
Determina si las siguientes fracciones son equivalentes o no:
Para saber si dos fracciones son equivalentes tienes que usar alguno de los tres métodos que hemos explicado anteriormente. Las correcciones las encontrarás resueltas por medio del primer procedimiento, aunque eres libre de utilizar el sistema que quieras.
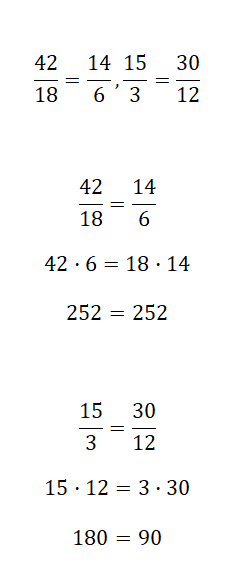
Ejercicio 4
Calcula las fracciones equivalentes de las siguientes expresiones:
En este último ejercicio tendrás que reescribir las expresiones que te proponemos (números enteros y números fraccionarios) en forma de fracción, procurando que mantenga una relación de equivalencia.