Los números complejos son un conjunto formado por números reales y números imaginarios. Estos dos últimos conjuntos numéricos pueden representarse gráficamente por medio de la recta real y la recta imaginaria. Y cuando situamos ambas rectas en un mismo plano, se forma el conocido plano complejo.
Contenido
¿Qué es el plano complejo?
El plano complejo está formado por el eje real (eje X), el cual es equivalente a la recta real y, por otro lado, el eje imaginario (eje Y), el cual conceptúa la recta imaginaria.
Cabe destacar, que este plano comprende todos los números complejos. Por lo tanto, da igual qué tan grande o tan pequeño, o en que forma esté escrito un número complejo, que este se puede graficar en el plano. Así que vamos a ver cómo se representan estos números en el plano complejo.
¿Cómo graficar números complejos en el plano complejo?
Como ya sabemos (o si no lo sabes, te recomendamos que leas nuestro artículo sobre los números complejos), existen tres formas de escribir un complejo: forma binómica, forma polar y forma trigonométrica. Cada una expresa el valor complejo siguiendo una estructura diferente, así que el método a seguir para hacer las representaciones gráficas es distinta.
A continuación, te explicamos el procedimiento a seguir en los tres casos:
Representación en forma binómica
Cuando tenemos un número complejo en notación binómica, que es la más habitual, debemos fijarnos en la estructura del número:
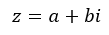
Donde, a es la parte real y b es la parte imaginaria.
Sabiendo esto, deducimos que el valor de a es el que utilizamos para la coordenada x (eje real) y el valor de b es el que usamos para la coordenada y (eje imaginario). Con el siguiente ejemplo, lo vas a entender mejor.
Vamos a tratar de representar el número: 3 + 2i.
Lo primero es dibujar el gráfico (señalizando que el eje horizontal es el real y el eje vertical es el imaginario):
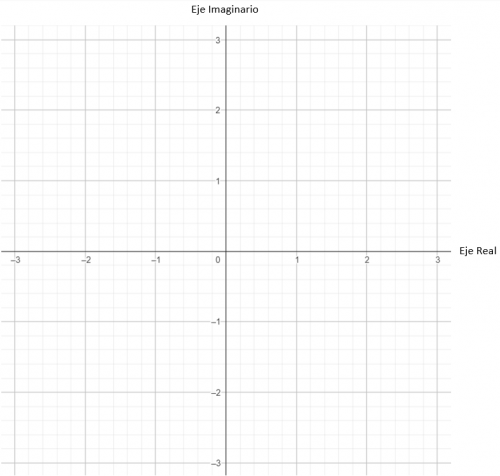
Después, ubicamos el punto del gráfico en coordenadas cartesianas (x, y), que hemos deducido a partido del número complejo. En este ejemplo práctico, nuestro punto es el (3, 2).

Así quedaría representado el valor 3 + 2i en el plano complejo.
Representación en forma polar
Ahora vamos a ver, cómo se representa un número complejo en forma polar. Para entender bien este método, debes saber que la notación polar define un número complejo a partir del módulo y del argumento. Los cuales se emplean en la representación gráfica como coordenadas polares (¡no coordenadas cartesianas!).
Y la característica principal del sistema de coordenadas polares es que se describe la ubicación de un punto, por medio de un vector y un ángulo (no como el anterior método). Los cuales se corresponden con el módulo y argumento de los números complejos. A continuación, te mostramos la fórmula universal de la forma polar de un número complejo:
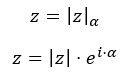
Donde |z| es el módulo y α es el argumento. Estas dos variables se traducen en el plano como:
- Módulo: es la longitud que define a un vector (entre el origen y el punto equivalente a nuestro número).
- Argumento: es el ángulo que forma el vector con el eje X.
Por lo tanto, el módulo de un número complejo se corresponde con la longitud del vector que utilizamos para hacer la representación gráfica. Mientras que el argumento o ángulo del número complejo, se corresponde con el ángulo que hay entre el vector y el eje X. A continuación, puedes ver un esquema que sitúa todas las variables:

Ahora, vamos a tratar de representar el número: 345.
Primero, debemos identificar el módulo y el argumento:
- Módulo: 3.
- Argumento: 45 grados.
Seguidamente, debemos encontrar los puntos de la gráfica que tienen un módulo igual a 3, en este caso nos sirve cualquier punto de una circunferencia de radio 3.
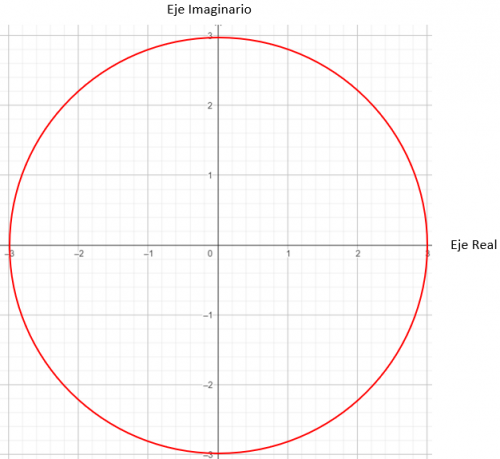
Y para acabar de determinar cuál es el punto exacto, debemos poner la condición de que el vector generado por el módulo y el origen deben hacer un ángulo de 45 grados con el eje X.

Y ya tenemos representado un número complejo en notación polar.
Representación en forma trigonométrica
Por último, nos queda explicar cómo se representa un número complejo en forma trigonométrica. Este caso y el anterior son prácticamente iguales, esto se debe a que tanto la forma polar como la forma trigonométrica, usan los mismos datos para expresar un número complejo: el módulo y el argumento. Solo cambia la estructura de la expresión:
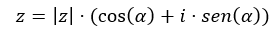
Donde, |z| es el módulo y α es el argumento.
Así que debemos aprovechar el mismo método que en el anterior caso: emplear el módulo como «longitud» y el argumento como el ángulo. Viendo el siguiente ejemplo, lo entenderás mejor.
Vamos a representar z = 4 · (cos (45) + i · sen(45)).
Lo primero es identificar el módulo y el ángulo:
- Módulo: 4.
- Argumento: 45 grados.
Después, debemos encontrar los puntos de la gráfica que tienen un módulo igual a 4, en este caso nos sirve cualquier punto de una circunferencia de radio 4.

Y finalmente, ubicamos el punto exacto, exigiendo que el ángulo formado entre el vector del módulo y el eje X sea de 45 grados, tal como nos dice el argumento.
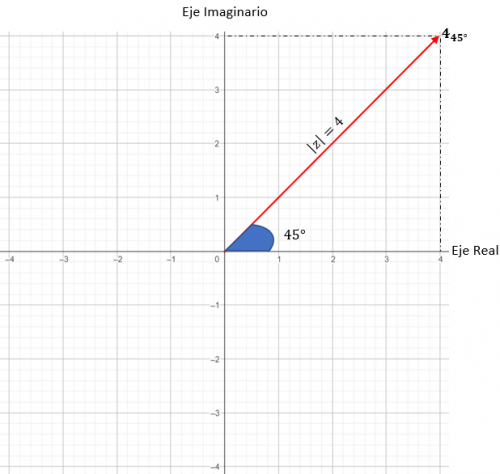
Y así representamos un número complejo en forma trigonométrica.
Ejercicio del plano complejo
Para acabar con esta publicación, te vamos a plantear un ejercicio final. Te recomendamos mucho que lo resuelvas, porque así consolidarás los conocimientos explicados a lo largo de este artículo.
Prueba de graficar los siguientes tres números complejos en el plano complejo:
z = 2 – i
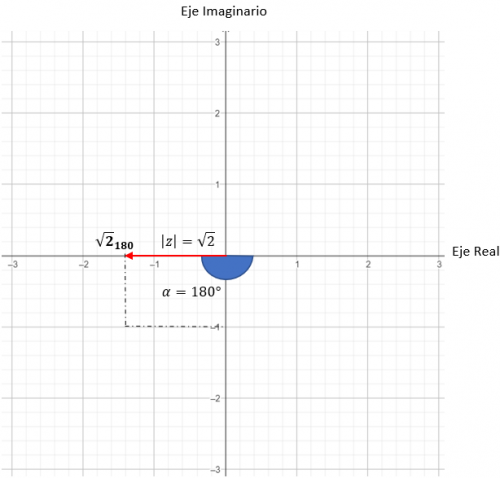
w = √2180
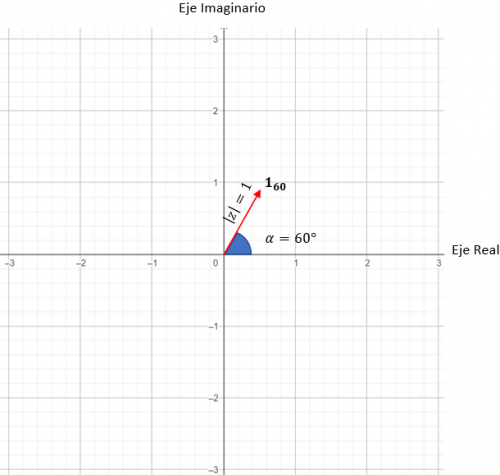
p = cos (60) + i · sen(60)