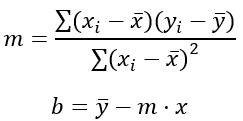Explicaciones matemáticas

La covarianza es una medida estadística que te ayuda a entender cómo dos variables cambian juntas. Imagina que tienes dos variables, como la temperatura y el consumo de helado. Si cuando la temperatura sube, el consumo de helado también sube, entonces las variables tienen una covarianza positiva. Si, por el contrario, cuando la temperatura sube, el consumo de helado baja, entonces tienen una covarianza negativa.

La covarianza te dice si las variables tienden a cambiar en la misma dirección (positiva) o en direcciones opuestas (negativa). Si no hay un patrón claro en cómo cambian juntas, entonces la covarianza será cercana a cero, lo que significa que no hay una relación lineal fuerte entre las variables.

¿Cómo se calcula la covarianza?

Para calcular la covarianza entre dos variables, necesitas tener un conjunto de datos que incluya los valores de ambas variables. Luego, sigue estos pasos:

1. Calcula la media (promedio) de cada variable. Suma todos los valores de cada variable y divide el resultado entre el número total de datos. Esto te dará la media de cada variable.
2. Resta la media de cada variable a cada valor correspondiente. Este paso implica restar la media de la variable X a cada valor de X, y hacer lo mismo para la variable Y.
3. Multiplica los resultados del paso anterior. Para cada valor restado en el paso anterior, multiplica el resultado correspondiente de la otra variable restada.
4. Suma los productos del paso anterior. Suma todos los productos obtenidos en el paso anterior para obtener un valor total.
5. Divide el valor obtenido en el paso anterior entre el número total de datos. Este valor es la covarianza entre las dos variables.

Recuerda que la covarianza puede ser positiva, negativa o cercana a cero. Una covarianza positiva indica que las variables tienden a cambiar en la misma dirección. Por otro lado, una covarianza negativa indica que las variables tienden a cambiar en direcciones opuestas. Finalmente, una covarianza cercana a cero indica que no hay un patrón claro en cómo cambian juntas.

Veamos un ejemplo para entender mejor

Imaginemos que tenemos dos variables, “horas de estudio” (X) y “calificación en un examen” (Y), y tenemos los siguientes datos para un grupo de 5 estudiantes:

Horas de estudio (X): 4, 6, 3, 7, 5.

Calificación en el examen (Y): 85, 90, 80, 95, 88.

Paso 1: Calcula la media de cada variable

Media de X: (4 + 6 + 3 + 7 + 5) ÷ 5 = 5

Media de Y: (85 + 90 + 80 + 95 + 88) ÷ 5 = 86

Paso 2: Resta la media de cada variable a cada valor correspondiente

X – Media de X: -1, 1, -2, 2, 0

Y – Media de Y: -1, 4, -6, 9, 2

Paso 3: Multiplica los resultados obtenidos en el paso anterior

(-1) · (-1) = 1

1 · 4 = 4

(-2) · (-6) = 12

2 · 9 = 18

0 · 2 = 0

Paso 4: Suma los productos obtenidos en el paso anterior

1 + 4 + 12 + 18 + 0 = 35

Paso 5: Divide el valor obtenido en el paso anterior entre el número total de datos

35 ÷ 5 = 7

Entonces, la covarianza entre las variables “horas de estudio” y “calificación en el examen” es 7.

¿Cuál es la diferencia entre la varianza y la covarianza?

La varianza es una medida que indica la dispersión estadística o variabilidad de un conjunto de datos. Se calcula como la media de los cuadrados de las desviaciones de los valores individuales con respecto a la media. Una varianza alta significa que los datos están dispersos o alejados de la media, mientras que una varianza baja significa que los datos están más cercanos a la media.

Por otro lado, la covarianza es una medida que indica cómo dos variables se mueven juntas. Es una medida de la variación conjunta de dos variables. Si la covarianza es positiva, indica que ambas variables tienden a aumentar o disminuir juntas. Si la covarianza es negativa, indica que una variable tiende a aumentar cuando la otra disminuye. Una covarianza cercana a cero indica que las variables no tienen una relación lineal fuerte.

En resumen, la varianza mide la variabilidad de un conjunto de datos en sí mismo, mientras que la covarianza mide la relación de variación conjunta entre dos variables.

¿Cuál es la importancia de la covarianza?

La covarianza es una medida importante en estadística y análisis de datos debido a varias razones. Generalmente, es utilizada para evaluar la fuerza y dirección de la relación entre dos variables. Un valor de covarianza cercano a cero indica una relación débil o nula, mientras que un valor alto en magnitud indica una relación fuerte entre las variables.

Por otro lado, cabe mencionar que, es una herramienta útil en la modelización y predicción de datos. Puede ser empleada en técnicas avanzadas de análisis de datos, como regresión lineal y análisis de series temporales, para entender cómo los cambios en una variable pueden afectar a otra variable.

Asimismo, tiene gran importancia en la gestión de riesgos financieros. Permite evaluar cómo se mueven dos activos financieros en conjunto, lo cual es fundamental en la diversificación de carteras de inversión y en la evaluación del riesgo y rendimiento de diferentes activos.

¿Cuáles son los principales usos de la covarianza?

La covarianza es una herramienta importante en el análisis de datos y tiene varios usos. Uno de los principales empleos de la covarianza es en la estadística y la econometría. Se utiliza para medir la relación de variación conjunta entre dos variables, lo que puede ayudarnos a entender cómo se mueven juntas.

En el campo de las finanzas, la covarianza es utilizada para evaluar la relación entre los rendimientos de diferentes activos financieros, como acciones, bonos o bienes raíces. Ayuda a los inversores a entender cómo se comportan los activos en conjunto y cómo se pueden diversificar las inversiones para gestionar el riesgo.

En el análisis de riesgo y gestión de carteras, la covarianza es utilizada para calcular la diversificación de riesgo, es decir, cómo se correlacionan los rendimientos de diferentes activos. Una baja covarianza entre dos activos indica que son menos propensos a moverse en la misma dirección, lo que puede ser beneficioso para reducir el riesgo de la cartera.

Además, la covarianza también se usa en áreas como la ciencia ambiental, la biología, la psicología y la ingeniería, donde se estudian las relaciones entre diferentes variables para comprender su comportamiento y hacer predicciones.

Es importante tener en cuenta que la covarianza tiene algunas limitaciones, como no ser una medida estandarizada y no capturar relaciones no lineales entre variables. Sin embargo, sigue siendo una herramienta valiosa en el análisis de datos para comprender cómo se mueven juntas dos variables y su relación de variación conjunta.

Propiedades de la covarianza

Veamos algunas de las propiedades más importantes de la covarianza, a continuación:

• La covarianza entre dos variables puede ser positiva, lo cual indica que tienden a moverse en la misma dirección. Por otro lado, si la covarianza es negativa, significa que tienden a moverse en direcciones opuestas. Si la covarianza es cero, no hay una relación lineal entre las variables.
• A diferencia de la correlación, la covarianza no está limitada a un rango específico y no tiene unidades de medida estandarizadas. Esto puede hacer que sea difícil comparar covarianzas de diferentes escalas o unidades.
• La presencia de valores extremos o atípicos en los datos puede tener un impacto significativo en la covarianza. Esto puede causar que la covarianza sea alta o baja, incluso si la relación entre las variables no es fuerte.
• La covarianza entre dos variables es simétrica, lo que significa que la covarianza de X con respecto a Y es igual a la covarianza de Y con respecto a X. Esto se debe a que la covarianza se basa en la variación conjunta de ambas variables.
• Es importante tener en cuenta que la covarianza no implica necesariamente una relación causal entre las variables. Solo muestra la dirección y magnitud de la variación conjunta entre las variables, pero no establece una relación causal directa.

Ejemplo de covarianza

Como ya sabemos, todo se entiende más claro cuando usamos ejemplos. Por ello, vamos a analizar este ejemplo sencillo de covarianza para una mejor comprensión.

Vamos a considerar dos nuevas variables, A y B, con los siguientes datos:

A = (a1, a2, a3) = (2, 5, 7)

B = (b1, b2, b3) = (6, 3, 1)

Primero, vamos a calcular la media aritmética de cada una de las variables:

A’ = (2 + 5 + 7) ÷ 3 = 4,67

B’ = (6 + 3 + 1) ÷ 3 = 3,33

Una vez que hemos calculado las medias aritméticas, procedemos a calcular la covarianza:

Cov(A, B) = (2 – 4,67) · (6 – 3,33) + (5 – 4,67) · (3 – 3,33) + (7 – 4,67) · (1 – 3,33) ÷ 3 = -2,33

En este caso, el valor de la covarianza es negativo. Esto indica que las variables A y B tienen una relación negativa, lo que significa que cuando una variable aumenta, la otra variable tiende a disminuir. Sin embargo, para comprender mejor la relación entre A y B, es necesario calcular la correlación lineal. 

También es relevante tener en cuenta que no se pueden comparar las covarianzas de variables diferentes, ya que la unidad de medida de la covarianza es la misma que la de las variables en cuestión. Por lo tanto, no se puede comparar la covarianza de variables como el ingreso y la edad, por ejemplo, debido a sus diferentes unidades de medida.

Los parámetros estadísticos son valores numéricos que resumen características importantes de un conjunto de datos y nos ayudan a comprender y describir la información que se encuentra en ellos. En palabras simples, podemos decir que son “etiquetas” que nos permiten entender mejor los datos y tomar decisiones basadas en ellos.

Dicho de otro modo, los parámetros estadísticos son medidas especiales utilizadas por los matemáticos y científicos para describir datos de manera sencilla. Básicamente, se tratan de herramientas que nos ayudan a entender los números de forma más fácil y clara.

Por ejemplo, supongamos que tienes una bolsa llena de caramelos y quieres saber cuántos caramelos hay en total. Ahí es donde los parámetros estadísticos entran en juego. La media es el promedio de caramelos, que se obtiene sumando todos los caramelos y dividiéndolos por la cantidad total. Esto te da una idea del número promedio de caramelos que puedes esperar encontrar.

Pero hay más, otro parámetro importante es la desviación estándar, que te ayuda a entender cuánto se alejan los caramelos del promedio. Te muestra qué tan diferentes son los caramelos en comparación con el número promedio.

Lo interesante es que los parámetros estadísticos también se pueden usar para hacer predicciones. Por ejemplo, si quieres saber cuántos caramelos habrá en la bolsa después de una semana, puedes emplear los parámetros estadísticos para estimarlo. Calculas el promedio de caramelos que tienes ahora y utilizas la desviación estándar para tener una idea de cuánto podría cambiar ese promedio en una semana.

¿Qué tipos de parámetros estadísticos existen?

En estadística, hay dos tipos principales de parámetros: los parámetros de tendencia central y los parámetros de dispersión.

Parámetros de tendencia central

Los parámetros de tendencia central nos dicen qué valor es típico o representativo en un conjunto de datos. Entre los parámetros de tendencia central tenemos tres medidas importantes:

• Media: la media se trata del valor cociente de la población (muestra).
• Mediana: por otro lado, tenemos la mediana que tiene como función dividir la muestra en dos partes, una superior y otra inferior. Dicho de forma sencilla, separa los datos en mitades.
• Moda: finalmente, la moda no es más que el valor más frecuente dentro de la muestra.

Vamos a utilizar un ejemplo numérico para explicar los parámetros de tendencia central usando la media, mediana y moda.

Supongamos que tienes las siguientes edades de un grupo de personas: 25, 30, 32, 35, 40, 40, 42, 45, 50.

La media es el promedio de las edades. Para calcularla, sumamos todas las edades y luego las dividimos entre el número total de edades. En este caso, sumamos 25 + 30 + 32 + 35 + 40 + 40 + 42 + 45 + 50 = 339, y luego dividimos entre 9 (qué es la cantidad de edades en el conjunto). La media es entonces 339 ÷ 9 = 37,67 años.

La mediana es el valor que está en el medio cuando las edades se ordenan de menor a mayor. En este caso, las edades ordenadas serían: 25, 30, 32, 35, 40, 40, 42, 45, 50. Como hay un número impar de edades, la mediana sería el valor que está en la posición central, que es 40 años.

La moda es el valor que aparece con mayor frecuencia en el conjunto de datos. En este caso, la moda es 40 años, ya que aparece dos veces, mientras que las demás edades aparecen solo una vez.

Entonces, en resumen, la media es 37,67 años, la mediana es 40 años y la moda es también 40 años.

Parámetros de dispersión

Por otro lado, los parámetros de dispersión nos indican qué tan dispersos o variados están los datos en un conjunto. Los más comunes son la varianza y la desviación estándar.

Varianza

La varianza mide qué tanto se pueden desviar los datos al cuadrado. En este caso, primero hay que elevar al cuadrado y, posteriormente, hacer el cálculo del promedio en cuestión. Veamos el siguiente ejemplo para entender mejor la explicación:

Supongamos que tienes las siguientes notas en un examen de cinco estudiantes: 80, 85, 90, 95, 100. Primero, calculamos la media sumando todas las notas y dividiendo entre el número total de estudiantes: (80 + 85 + 90 + 95 + 100) ÷ 5 = 90.

Luego, para calcular la varianza, restamos la media de cada nota y elevamos al cuadrado los resultados. Después, promediamos los resultados elevados al cuadrado. En este caso, los cálculos serían:

(80 – 90)² = 100

(85 – 90)² = 25

(90 – 90)² = 0

(95 – 90)² = 25

(100 – 90)² = 100

Sumamos los resultados: 100 + 25 + 0 + 25 + 100 = 250. Y luego lo dividimos entre el número total de datos (5) para obtener el promedio: 250 ÷ 5 = 50.

Entonces, la varianza en este caso es 50. Esto nos indica que, en promedio, las notas se alejan en promedio 50 unidades al cuadrado de la media, lo cual representa la dispersión o variabilidad de los datos en relación con la media.

Desviación estándar

Como hemos estudiado antes, la desviación estándar se define simplemente como el resultado de la raíz cuadrada de la varianza. Cabe mencionar que, este tipo de parámetro de dispersión es mucho más efectivo realizando estimaciones con respecto a la desviación media en el caso de distribución normal.

Tomemos el ejemplo anterior de las notas en un examen: 80, 85, 90, 95, 100. La varianza ya la calculamos y es 50. Para obtener la desviación estándar, simplemente tomamos la raíz cuadrada de la varianza.

√50 ≈ 7,07

Entonces, la desviación estándar en este caso es aproximadamente 7,07. Esto nos indica que, en promedio, las notas se alejan aproximadamente 7,07 unidades de la media, pero en la misma unidad de medida que las notas originales. Es una medida más fácil de interpretar y comparar con los datos originales, ya que está en la misma escala.

Cuantiles

Además de las medidas anteriores, tenemos también en los parámetros de dispersión. Los cuantiles tienen como función, la división de la muestra n en secciones equivalentes. Gracias a esto, es posible estimar los rangos en los que existe una mayor concentración de valores. De acuerdo con el valor de n los cuantiles se definen de distintas maneras.

• Deciles: se encargan de separar el conjunto de datos en diez secciones iguales.
• Cuartiles: funciona igual que el modelo anterior, solo que el lugar de diez, divide en cuatro secciones.
• Percentiles: por último, los percentiles se utilizan para separar los datos de un conjunto en 100 secciones idénticas.

¿Para qué sirven los parámetros estadísticos?

Como bien mencionamos antes, los parámetros estadísticos tienen mucha importancia y su utilización es bastante amplia. A continuación, te presentamos algunas de sus aplicaciones más importantes.

Economía

Los parámetros estadísticos se usan para analizar indicadores económicos, como el PIB, la tasa de desempleo, la inflación, entre otros. Estos parámetros permiten medir la salud económica de un país o región, identificar tendencias y hacer predicciones para la toma de decisiones en política económica.

Ciencias de la Salud

En este caso, se utilizan en estudios clínicos y epidemiológicos para analizar datos de salud, como la prevalencia de una enfermedad, la eficacia de un tratamiento, el impacto de factores de riesgo, entre otros. Estos parámetros son fundamentales para la toma de decisiones en la prevención, diagnóstico y tratamiento de enfermedades.

Ciencias Sociales

Por otro lado, los parámetros estadísticos son útiles en disciplinas como la psicología, sociología, educación, entre otras, para analizar datos sobre comportamiento humano, actitudes, opiniones, entre otros. Estos parámetros permiten obtener insights y realizar inferencias sobre la población estudiada.

Marketing y Publicidad

Además de lo anterior, en el mundo de la publicidad, también son muy importantes. En este caso, son utilizados para analizar datos de mercado, como la segmentación de clientes, el análisis de preferencias y comportamientos de consumo, la evaluación de campañas publicitarias, entre otros. Estos parámetros ayudan a entender y tomar decisiones informadas en estrategias de marketing y publicidad.

Investigación Científica

Además, son utilizados en diversos campos de la investigación científica, como la biología, la física, la química, entre otros, para analizar datos experimentales, realizar inferencias y validar resultados. Estos parámetros son esenciales para el rigor y la validez de la investigación científica.

Finanzas

Se utilizan también, para analizar datos financieros, como la rentabilidad de una inversión, la volatilidad de un activo, la evaluación de riesgos, entre otros. Estos parámetros son utilizados para la toma de decisiones en la gestión de inversiones, planificación financiera y evaluación de riesgos.

Ingeniería

Finalmente, son ideales en diversos campos de la ingeniería, como la ingeniería de calidad, la ingeniería de procesos, la ingeniería de sistemas, entre otros, para analizar datos de producción, calidad, rendimiento y optimización de procesos. Estos parámetros son utilizados para la mejora continua y la toma de decisiones en la gestión de proyectos y la optimización de sistemas.

Ejemplo de parámetros estadísticos

Teniendo en cuenta la información anterior, es tiempo de utilizar un ejemplo para reforzar mejor lo aprendido. Veamos, a continuación.

1.  Ejemplo Media (Promedio)

Supongamos que tienes una lista de calificaciones de 5 estudiantes en un examen de matemáticas: 7, 8, 9, 6, y 10. Para encontrar la media o promedio, sumamos todas las calificaciones y luego las dividimos por el número de estudiantes:

7 + 8 + 9 + 6 + 10 = 40

Media = 40 ÷ 5 = 8

Por lo tanto, la media o promedio de las calificaciones de estos 5 estudiantes es 8.

2.  Ejemplo Mediana

Supongamos que tienes una lista de edades de un grupo de 7 personas: 12, 14, 15, 13, 12, 16 y 18. Para encontrar la mediana, primero ordenamos las edades de forma ascendente: 12, 12, 13, 14, 15, 16, 18

Luego, encontramos el valor central de la lista, que en este caso es 14. Por lo tanto, la mediana de las edades de este grupo de personas es 14.

3.  Ejemplo Moda

Supongamos que tienes una lista de colores de camisetas que usan un grupo de 10 personas: rojo, azul, verde, rojo, amarillo, azul, verde, verde, rojo, azul. La moda es el valor que aparece con mayor frecuencia en la lista. En este caso, el color verde aparece 3 veces, mientras que los otros colores solo aparecen 2 veces o menos. Por lo tanto, la moda de los colores de las camisetas es verde.

4.  Ejemplo de percentiles

Supongamos que tienes un conjunto de datos que representa las alturas en centímetros de un grupo de 20 estudiantes de secundaria. Quieres encontrar el percentil 75, que representa el valor por debajo del cual se encuentra el 75% de las alturas. Después de ordenar los datos, encuentras que el valor correspondiente al percentil 75 es 168 cm. Esto significa que el 75% de los estudiantes tienen una altura de 168 cm o menos.

5.  Ejemplo Varianza

Supongamos que tienes un conjunto de datos que representa la cantidad de horas de estudio diario de un grupo de 10 estudiantes para un examen. Los datos son: 2, 3, 4, 2, 5, 3, 4, 1, 2, 3. Para calcular la varianza, primero calculas la media, que es 2,7 horas. Luego, restas la media a cada valor, lo elevas al cuadrado y lo sumas todo. Finalmente, divides la suma por el número de datos:

((2-2,7)² + (3-2,7)² + (4-2,7)² + (2-2,7)² + (5-2,7)² + (3-2,7)² + (4-2,7)² + (1-2,7)² + (2-2,7)² + (3-2,7)²) ÷ 10 = 1,61

Por lo tanto, la varianza de las horas de estudio de este grupo de estudiantes es 1,61.

6.  Ejemplo Desviación estándar

Continuando con el ejemplo anterior, para encontrar la desviación estándar, simplemente sacas la raíz cuadrada de la varianza:

√1,61 ≈ 1,27

Por lo tanto, la desviación estándar de las horas de estudio de este grupo de estudiantes es de aproximadamente 1,27 horas.

¿Alguna vez te has preguntado qué tan probable es que algo suceda? Calcular la probabilidad es una herramienta que nos ayuda a entender y medir la posibilidad de que un evento ocurra.

Es una forma de expresar las chances de que algo suceda o no suceda, y se utiliza en muchos aspectos de la vida cotidiana, desde predecir el clima hasta tomar decisiones en juegos de azar. En este texto, vamos a explorar mucho más sobre la probabilidad y cómo se puede calcular para obtener una idea más clara de las posibles ocurrencias de eventos.

¿Qué son las probabilidades?

Las probabilidades son una manera de medir qué tan probable es que algo ocurra. En otras palabras, son una forma de estimar las posibilidades de que algo suceda o no suceda.

En general, se utilizan para predecir lo que podría ocurrir en el futuro, o para hacer suposiciones basadas en la información disponible en el presente. Las probabilidades son útiles en muchas situaciones de la vida cotidiana, como en juegos de azar, pronósticos del clima, decisiones comerciales, deportivas y muchas más.

Básicamente, se consideran una herramienta emocionante que nos ayuda a entender el mundo que nos rodea y tomar decisiones informadas en el día a día.

¿Qué tipos de probabilidades existen?

Antes que nada, debes tener presente que hay distintos tipos de probabilidades y que cada una tiene una utilidad diferente. Veamos a continuación, los tipos de probabilidad que existen.

• Matemática: Se basa en principios lógicos y no experimentales, calculando numéricamente eventos aleatorios en un campo determinado.
• Frecuencial: Se obtiene a través de la experimentación, contando el número de veces que un suceso ocurre en un número específico de oportunidades.
• Objetiva: Considera de antemano la frecuencia de un evento, revelando solo los casos probables en los que puede ocurrir.
• Binomial: Determina el éxito o fracaso de un evento con solo dos posibles resultados.
• Lógica: Plantea la posibilidad de que un evento ocurra basándose en leyes inductivas.
• Condicionada: Explica la probabilidad de que ocurra un evento en función de la ocurrencia previa de otro evento, donde uno depende del otro.
• Hipergeométrica: Se obtiene a través de técnicas de muestreo, clasificando los eventos según su frecuencia de aparición en grupos determinados.

¿Cómo se calculan las probabilidades?

Para calcular la probabilidad, hay que tener siempre presente que este concepto no es más que un cálculo matemático que estima las posibilidades de que un evento suceda o no cuando tiene que ver con el azar. Por ejemplo, si giras una ruleta de número, ¿En qué número se detendrá?

Supongamos que la ruleta tiene un total de cinco números, por ende, puede pararse en un número desde el uno hasta el cinco. En este punto, sin saberlo, se construye lo que se conoce como experimento (la acción de girar la ruleta) y, además, un espacio muestral constituido por los números en cuestión.

Entiéndase el espacio muestral como un grupo que reúne los sucesos que podrían ocurrir. Teniendo este ejemplo, es posible pensar que la ruleta se detendrá en cualquiera de los cinco números que lo conforman, en cambio, es imposible que se pare en el número 8, por ejemplo.

Después de analizar este pequeño ejemplo, pasemos al análisis para el cálculo de las probabilidades. Para hacerlo, basta con usar estos pasos:

• Para eventos igualmente probables: Divide el número de resultados favorables al evento entre el número total de posibles resultados.
• Para eventos con frecuencias: Divide el número de veces que el evento ocurre entre el número total de oportunidades.
• Para eventos condicionados: Multiplica la probabilidad del evento previo por la probabilidad del evento condicionado.
• Para eventos binomiales: Usa la fórmula binomial que involucra la probabilidad de éxito, la probabilidad de fracaso y el número de intentos.
• Para eventos hipergeométricos: Usa la fórmula hipergeométrica que considera el tamaño de la muestra estadística y la cantidad de eventos favorables.

Veamos este ejemplo:

Imagina que tienes una bolsa con 10 caramelos de colores: 4 caramelos rojos, 3 caramelos verdes y 3 caramelos azules. Quieres saber la probabilidad de sacar un caramelo rojo al azar.

Paso 1: Identifica el evento y los posibles resultados. El evento es sacar un caramelo rojo y los posibles resultados son los 10 caramelos en total.

Paso 2: Cuenta los resultados favorables. En este caso, hay 4 caramelos rojos, así que el número de resultados favorables es 4.

Paso 3: Calcula la probabilidad. Divide el número de resultados favorables (4) entre el número total de posibles resultados (10).

Probabilidad de sacar un caramelo rojo = 4 ÷ 10 = 0,4 o 40%

¡Así de simple! La probabilidad de sacar un caramelo rojo al azar es del 40%. Puedes aplicar estos pasos para calcular probabilidades en diferentes situaciones y eventos.

¿Cuáles son los principales usos de las probabilidades?

Las probabilidades tienen una amplia gama de aplicaciones en diferentes áreas de la vida cotidiana y en diversos campos del conocimiento. Algunos de los principales usos de las probabilidades son:

• Estadísticas: para analizar y representar datos, calcular promedios, desviaciones estándar, y realizar inferencias sobre poblaciones basadas en muestras.
• Juegos de azar: en juegos de azar como loterías, casinos y apuestas deportivas para calcular las posibilidades de ganar o perder en diferentes situaciones y tomar decisiones informadas.
• Gestión de riesgos: evaluar la probabilidad de que ocurran eventos indeseables, como accidentes, desastres naturales o enfermedades, y planificar estrategias de mitigación y prevención.
• Finanzas: para modelar y evaluar riesgos de inversión, calcular primas de seguros, valorar activos financieros y planificar estrategias de gestión de cartera.
• Ciencias naturales: en ciencias naturales, como la física y la biología, para modelar y predecir eventos aleatorios, como la descomposición de partículas radioactivas o la probabilidad de mutaciones genéticas.
• Ciencias sociales: para estudiar el comportamiento humano, la toma de decisiones y la probabilidad de ocurrencia de eventos sociales, como elecciones o encuestas de opinión.
• Tecnología: para modelar y predecir eventos, como el reconocimiento de patrones en imágenes o la predicción del comportamiento del usuario en una plataforma.

Estos son solo algunos ejemplos de los principales usos de las probabilidades en diferentes áreas de la vida cotidiana y en diversos campos del conocimiento.

Las probabilidades son una herramienta poderosa para comprender y analizar situaciones inciertas y tomar decisiones informadas basándonos en la probabilidad de que ocurran eventos específicos.

¿Qué teorías explican la probabilidad?

Además de lo anterior, es importante destacar que existen varias teorías que pueden explicar un poco mejor las probabilidades. Veamos las más relevantes, a continuación.

• Clásica: establece que la probabilidad de un evento se calcula dividiendo el número de resultados favorables entre el número total de resultados posibles. Es aplicable cuando todos los resultados son igualmente probables y se basa en la idea de equiprobabilidad.
• Frecuencial: se basa en la idea de que la probabilidad de un evento se puede estimar observando la frecuencia con la que ocurre en una serie de experimentos o ensayos repetidos. Cuanto mayor sea el número de ensayos, más precisas serán las estimaciones de probabilidad.
• Subjetiva: se centra en la idea de que la probabilidad es una medida subjetiva basada en la creencia o el grado de confianza de una persona en que un evento ocurra. Se basa en la idea de que la probabilidad puede variar de una persona a otra según sus conocimientos, experiencias y creencias individuales.
• Axiomática: se basa en una serie de axiomas o principios matemáticos que establecen reglas formales para calcular la probabilidad. Algunos ejemplos de axiomas son el axioma de la unidad, que establece que la probabilidad de que ocurra un evento seguro es igual a 1, y el axioma de la aditividad, que establece reglas para calcular la probabilidad de eventos combinados.

Ejemplos gráficos de las probabilidades

Finalmente, para entender mejor de qué se tratan las probabilidades, pasemos a revisar algunos ejemplos simples.

Ejemplo 1: Lanzamiento de un dado.

Supongamos que tienes un dado de seis caras numeradas del 1 al 6. ¿Cuál es la probabilidad de obtener un número par al lanzar el dado?

Solución:

Resultados favorables: Los números pares en el dado son 2, 4 y 6, lo que hace un total de 3 resultados favorables.

Resultados posibles: El dado tiene 6 caras en total, lo que hace un total de 6 resultados posibles.

Entonces, la probabilidad de obtener un número par al lanzar el dado es:

3 resultados favorables ÷ 6 resultados posibles = 0,5 o 50%

Ejemplo 2: Sacar una carta de una baraja.

Supongamos que tienes una baraja de 52 cartas y quieres saber la probabilidad de sacar una carta roja al azar.

Solución:

Resultados favorables: En una baraja estándar de 52 cartas, hay 26 cartas rojas (13 corazones y 13 diamantes), lo que hace un total de 26 resultados favorables.

Resultados posibles: La baraja tiene un total de 52 cartas.

Entonces, la probabilidad de sacar una carta roja al azar de la baraja es:

26 resultados favorables ÷ 52 resultados posibles = 0,5 o 50%

Ejemplo 3: Probabilidad de acertar una pregunta de opción múltiple

Supongamos que tienes un examen con 5 preguntas de opción múltiple, cada una con 4 opciones de respuesta (A, B, C, D), y solo una opción es correcta en cada pregunta. Si respondes al azar en cada pregunta, ¿cuál es la probabilidad de acertar al menos una pregunta?

Solución:

Para calcular la probabilidad de acertar al menos una pregunta, necesitamos calcular la probabilidad de NO acertar ninguna pregunta y luego restarla de 1 (ya que la probabilidad de acertar al menos una pregunta es complementaria a la probabilidad de NO acertar ninguna).

Probabilidad de NO acertar ninguna pregunta:

La probabilidad de NO acertar una pregunta es de 3 respuestas incorrectas de 4 posibles (ya que solo una opción es correcta), lo que hace un total de (3 ÷ 4) de probabilidad de NO acertar en cada pregunta.

Entonces, la probabilidad de NO acertar ninguna pregunta en las 5 preguntas sería: (3 ÷ 4)⁵ = 0,2373

Probabilidad de acertar al menos una pregunta:

Restamos la probabilidad de NO acertar ninguna pregunta de 1:

1 – 0,2373 = 0,7627 o 76,27%

El método de los mínimos cuadrados es una herramienta matemática para encontrar la mejor línea recta que se ajuste a un conjunto de puntos. Te lo explicamos de manera sencilla:

Imagina que tienes un conjunto de puntos en un gráfico dispersos por aquí y por allá. Quieres encontrar una línea recta que “se ajuste” lo mejor posible a esos puntos, de manera que minimice la distancia entre la línea y los puntos. Esa es la idea detrás del método de los mínimos cuadrados.

El método utiliza una fórmula para calcular la ecuación de la línea que minimiza la suma de los cuadrados de las diferencias entre los puntos y la línea. Es decir, busca la línea que tenga la menor “desviación” respecto a los puntos.

En palabras simples, el método de los mínimos cuadrados es útil para el análisis de datos arrojados en una investigación, con el objetivo de expresar cómo se comportan de forma lineal, reduciendo los errores de la información sustraída.

¿Quién creó el método de los mínimos cuadrados?

El método de los mínimos cuadrados, una herramienta fundamental en estadística y análisis de datos, se atribuye al matemático alemán Carl Friedrich Gauss, quien lo propuso en 1794. Sin embargo, Gauss no lo publicó hasta 1809.

Curiosamente, el matemático francés Andrien-Marie Legendre publicó una versión similar en 1805, desarrollándolo de forma independiente.

Ambos matemáticos contribuyeron a la creación de este método que ha sido ampliamente utilizado en diversas disciplinas para ajustar modelos a datos observados y hacer predicciones precisas.

Fórmula del método de mínimos cuadrados

Sin duda, para entender lo que implica este método, es esencial explicar su fórmula y proceso de realización. Aquí tienes una explicación detallada de la fórmula del método de los mínimos cuadrados:

Definir el problema

Supongamos que tienes un conjunto de datos con dos variables, una variable independiente (x) y una variable dependiente (y), y quieres ajustar una línea recta a esos datos.

El objetivo es encontrar los valores de los coeficientes de la ecuación de la línea (intercepto y pendiente) que minimicen la suma de los cuadrados de las diferencias entre los valores reales de y, y los valores predichos por la línea ajustada.

Calcular la ecuación de la línea

La ecuación de una línea recta tiene la forma y = mx + b, donde m es la pendiente y b es el intercepto. La fórmula del método de los mínimos cuadrados para calcular los valores de m y b es la siguiente:

Donde:

Σ representa la suma de los valores.

x_i y y_i son los valores de las variables x e y respectivamente para cada punto de datos.

x̄ y ȳ son las medias de los valores de x e y respectivamente.

(x_i – x̄) y (y_i – ȳ) son las diferencias entre los valores de x e y y sus medias respectivas.

(x_i – x̄)² es el cuadrado de la diferencia entre el valor de x y su media.

Interpretar los resultados

Una vez que has calculado los valores de m y b usando la fórmula, puedes utilizarlos para obtener la ecuación de la línea recta ajustada. Por ejemplo, si obtuviste m = 2 y b = 3, entonces la ecuación de la línea ajustada sería y = 2x + 3. Esto te permite hacer predicciones o estimaciones de los valores de y para diferentes valores de x en función de la línea ajustada.

¿En qué casos se usa el método de mínimos cuadrados?

Seguramente, te preguntarás ¿Cuándo se emplea este método? ¡Es muy útil en varias situaciones! Por ejemplo, cuando quieres analizar datos experimentales o de investigación para encontrar una relación o tendencia.

Supongamos que estás investigando cómo el precio de una casa está relacionado con su tamaño en metros cuadrados. Podrías utilizar el método de mínimos cuadrados para encontrar la línea recta que mejor se ajuste a los datos y te dé una idea clara de esa relación.

También se usa en la economía para modelar y predecir variables como la demanda de productos o el comportamiento de los precios. Además, en la ingeniería, el método de mínimos cuadrados se aplica para ajustar modelos matemáticos a datos de pruebas o simulaciones.

El método de mínimos cuadrados es una herramienta poderosa y versátil que se emplea en muchas áreas de estudio y trabajo para analizar datos y encontrar relaciones importantes.

Aplicaciones del método de mínimos cuadrados en otros teoremas

Además de su utilización en sí mismo, el método de mínimos cuadrados es bastante útil en otros teoremas. Veamos un poco más sobre el tema, a continuación.

Teorema de Regresión

Es ampliamente usado en el teorema de regresión para encontrar la mejor línea que se ajuste a un conjunto de datos. Por ejemplo, puedes emplearlo para analizar la relación entre la altura de una planta y la cantidad de luz que recibe para determinar cómo la planta crecerá en diferentes condiciones de luz.

Teorema de Interpolación

En este caso, el método de mínimos cuadrados también se aplica en el teorema de interpolación para encontrar la función polinómica que mejor se ajuste a un conjunto de puntos. Por ejemplo, puedes utilizarlo para aproximar la trayectoria de un objeto en movimiento basado en datos de posición y tiempo.

Teorema de Ajuste de Curvas

Sirve en el teorema de ajuste de curvas para encontrar una curva que se ajuste a un conjunto de datos. Esto es útil en aplicaciones como el modelado de datos climáticos para predecir el cambio climático o en la predicción de la trayectoria de un proyectil.

Teorema de Análisis de Fourier

En el teorema de análisis de Fourier, el método de mínimos cuadrados se usa para aproximar una función periódica a partir de una serie de datos discretos. Esto se aplica en la señalización de datos y en la compresión de imágenes y sonido.

Teorema de Regresión No Lineal

Finalmente, el método de mínimos cuadrados también se aplica en el teorema de regresión no lineal para encontrar la mejor curva que se ajuste a un conjunto de datos que no sigue una relación lineal. Por ejemplo, puedes emplearlo para analizar cómo la concentración de un producto químico afecta la tasa de reacción.

Ejemplo del método de mínimos cuadrados

Para comprender mejor la forma en que puedes aplicar el método de mínimos cuadrados, observemos un ejemplo, a continuación.

Supongamos que tienes los siguientes datos de altura (en centímetros) de una planta en diferentes semanas:

Quieres encontrar la mejor línea recta que se ajuste a estos datos para hacer una predicción de la altura futura de la planta.

Paso 1: Graficar los datos

Lo primero que debes hacer es graficar los datos en un gráfico de dispersión. El eje x representará las semanas y el eje y representará la altura en centímetros. Aquí está el gráfico:

Paso 2: Aplicar el método de mínimos cuadrados

El método de mínimos cuadrados busca encontrar una línea recta que minimice la suma de los cuadrados de las diferencias entre los datos reales y los valores predichos por la línea. En este caso, la línea se representa por la ecuación de una recta: y = mx + b, donde “y” es la altura, “x” son las semanas, “m” es la pendiente de la línea y “b” es el intercepto en el eje y.

Para encontrar los valores de “m” y “b” que minimicen la suma de los cuadrados de las diferencias, se utilizan las siguientes fórmulas:

Donde N es el número de datos (en este caso, 6), Σxy es la suma del producto de las semanas por las alturas, Σx es la suma de las semanas, Σy es la suma de las alturas, y Σx² es la suma de los cuadrados de las semanas.

Aplicando estas fórmulas a los datos de altura, se obtiene:

Σxy = 1·10 + 2·12 + 3·14 + 4·16 + 5·18 + 6·20 = 630

Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21

Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90

Σx² = 1² + 2² + 3² + 4² + 5² + 6² = 91

Sustituyendo estos valores en las fórmulas de “m” y “b”:

m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21²) ≈ 2,07

b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24

Por lo tanto, la ecuación de la línea recta que se ajusta a los datos de altura es: y.

La varianza es una medida estadística que nos dice cuánto se dispersan los datos alrededor de la media. Es como medir qué tan “esparcidos” están los datos en relación con el valor promedio.

Imagina que tienes una lista de números, como las calificaciones de un examen. La varianza te ayuda a entender qué tan diferentes son estas calificaciones entre sí. Si las calificaciones están muy cerca unas de otras, la varianza será baja. Pero si hay muchas diferencias entre las calificaciones, la varianza será alta.

En líneas generales, la varianza es una herramienta útil para entender la dispersión de datos en un conjunto de valores. Si la varianza es alta, significa que los datos están más dispersos, mientras que, si es baja, significa que los datos están más cercanos entre sí.

¿Cómo se calcula la varianza?

Para calcular la varianza, necesitas hacer algunos pasos matemáticos, pero no te preocupes, es más sencillo de lo que parece. Primero, necesitas calcular la media o promedio de los datos. Luego, resta cada dato de la media y eleva al cuadrado cada diferencia. Luego, sumas todos estos cuadrados y los divides por la cantidad de datos. Esa es la varianza.

Para entender un poco mejor esto, veamos un ejemplo sobre el cálculo de la varianza, a continuación:

Paso 1: Obtén los datos

Supongamos que tienes los siguientes datos: 5, 7, 9, 11, 13. Estos son los valores de una muestra de datos que deseas calcular su varianza.

Paso 2: Calcula la media

Suma todos los valores y divide entre la cantidad total de datos para obtener la media:

Media = (5 + 7 + 9 + 11 + 13) ÷ 5 = 45 ÷ 5 = 9

La media de los datos es 9.

Paso 3: Resta la media a cada dato

Resta la media obtenida en el paso anterior a cada dato en la lista:

5 – 9 = -4

7 – 9 = -2

9 – 9 = 0

11 – 9 = 2

13 – 9 = 4

Paso 4: Eleva al cuadrado cada diferencia

Eleva al cuadrado cada una de las diferencias obtenidas en el paso anterior:

(-4)² = 16

(-2)² = 4

0² = 0

2² = 4

4² = 16

Paso 5: Suma los cuadrados de las diferencias

Suma todos los resultados obtenidos en el paso anterior:

16 + 4 + 0 + 4 + 16 = 40

Paso 6: Divide por la cantidad de datos

Divide la suma de los cuadrados de las diferencias entre la cantidad total de datos (en este caso, 5):

Varianza = 40 ÷ 5 = 8

La varianza de los datos es 8.

¿Cuál es la fórmula de la varianza?

Antes de analizar este punto, es importante mencionar que la varianza tiene gran importancia para la estadística. A pesar de que se trate de una medida bastante simple, aporta información de interés en función de una variable específica.

La unidad de medida siempre será la que corresponde a los datos, pero al cuadrado. Asimismo, hay que señalar que la varianza es siempre igual a cero o mayor que este. Lo anterior se debe a que los residuos siempre se elevan al cuadrado, por lo que, en términos matemáticos, es imposible que exista varianza negativa.

Teniendo esto en cuenta, a continuación, te mostramos la fórmula de la varianza:

S² = varianza

x _i = término de conjunto de datos

X̄ = medida de la muestra

∑ = sumatoria

n = tamaño de la muestra

¿Qué es la varianza alta y baja?

La varianza se considera alta cuando los datos en una muestra estadística o población están dispersos y se alejan mucho de la media. Esto significa que los valores individuales en los datos están ampliamente distribuidos y hay una gran variabilidad en los mismos.

Por otro lado, la varianza se considera baja cuando los datos en una muestra o población están más cercanos a la media y hay poca dispersión entre los valores individuales. Esto implica que los datos son más consistentes y tienen una menor variabilidad.

¿Cuáles son los principales usos de la varianza?

La varianza es una medida estadística ampliamente utilizada en diversos campos debido a su capacidad para evaluar la dispersión o variabilidad de los datos en una muestra. Algunos de los principales usos de la varianza son:

En estadística descriptiva: para describir la dispersión de los datos en una muestra, lo que permite entender cómo los valores individuales se alejan de la media y cómo se distribuyen en la muestra.

En estadística inferencial: para estimar la variabilidad de los datos en una población a partir de una muestra, lo que permite hacer inferencias sobre la población en general.

En finanzas: en el análisis de riesgo y rendimiento de inversiones, donde una mayor varianza indica mayor riesgo y una menor varianza indica menor riesgo en una cartera de inversiones.

En investigación científica: analizar la variabilidad de datos en estudios científicos, como en la investigación médica, la biología, la psicología y otras disciplinas, para comprender la variabilidad de los resultados y la consistencia de los datos.

En la calidad del control de procesos: en el control de calidad de procesos industriales para medir la variabilidad de los productos o servicios producidos, lo que permite identificar problemas en la consistencia y calidad del proceso.

En la econometría: en la modelización y análisis de datos económicos para entender la variabilidad de las variables económicas y evaluar la confiabilidad de los modelos econométricos.

¿Cuál es la importancia de la varianza?

La varianza es importante porque te permite comprender la variabilidad de los datos en una muestra. Si la varianza es alta, significa que los datos están dispersos y hay mucha variabilidad. Esto es relevante para tomar decisiones informadas en áreas como inversiones, gestión de riesgos y análisis de datos.

Además, la varianza te ayuda a entender la consistencia de los datos en una muestra o población. Una varianza baja indica que los datos son consistentes y tienen poca variabilidad, mientras que una varianza alta indica que los datos son menos consistentes y tienen más variabilidad.

¿Es lo mismo la desviación estándar y la varianza?

La desviación estándar y la varianza son dos medidas estadísticas relacionadas que describen la dispersión o variabilidad de los datos en una muestra o población. La principal diferencia entre ellas es la unidad de medida y la interpretación de los resultados.

La varianza es una medida que representa la dispersión de los datos respecto a su media, calculada como la suma de los cuadrados de las desviaciones de los valores individuales respecto a la media, dividida por el número total de datos.

Se calcula elevando al cuadrado las diferencias entre cada valor y la media, sumándolas y dividiéndolas por el tamaño de la muestra o población. La varianza se expresa en unidades al cuadrado y puede ser difícil de interpretar directamente debido a que está en una escala diferente a los datos originales.

Por otro lado, la desviación estándar no es otra cosa que la raíz cuadrada de la varianza. Se calcula como la raíz cuadrada positiva de la varianza. La desviación estándar se expresa en las mismas unidades que los datos originales y es una medida más intuitiva de la dispersión de los datos.

Una desviación estándar más alta indica mayor dispersión o variabilidad de los datos, mientras que una desviación estándar más baja indica menor dispersión o variabilidad.

Varianza para datos agrupados

La varianza para datos agrupados se refiere al cálculo de la variabilidad o dispersión de datos que se encuentran agrupados en intervalos o clases. En lugar de tener datos individuales, como en el caso de la varianza para datos no agrupados, se tienen rangos o intervalos en los cuales se encuentran los datos.

El cálculo de la varianza para datos agrupados se realiza utilizando una fórmula ligeramente diferente. Primero, se calcula el punto medio de cada intervalo, que es el promedio del límite inferior y superior de cada intervalo. Luego, se calcula la media ponderada de los puntos medios, empleando las frecuencias relativas o absolutas de los intervalos como pesos.

A partir de esta media ponderada, se calcula la varianza utilizando la misma fórmula que para datos no agrupados, es decir, como la media de los cuadrados de las diferencias entre los valores individuales y la media ponderada.

La varianza para datos agrupados es útil cuando se trabaja con conjuntos de datos que se presentan en forma de intervalos o clases, como en el caso de datos demográficos, económicos o cualquier otro tipo de datos que se encuentren agrupados en categorías o rangos.

Propiedades de la varianza

La varianza es una medida estadística que tiene varias propiedades importantes. Algunas de las principales propiedades de la varianza son:

• Siempre es un valor no negativo, ya que está definida como el promedio de los cuadrados de las diferencias entre los datos individuales y la media.
• Es sensible a los valores extremos o atípicos en los datos, ya que implica el cuadrado de las diferencias.
• Tiene unidades cuadráticas, lo que implica que está en la misma unidad al cuadrado que los datos originales.
• Puede ser afectada por valores atípicos o datos extremos, lo que puede hacer que sea una medida no robusta de la variabilidad de los datos.
• Si los datos son independientes y no están correlacionados entre sí, la varianza de la suma de dos conjuntos de datos es igual a la suma de las varianzas de los dos conjuntos de datos.

Ejemplos de varianza

Ahora que tenemos claro el concepto de varianza y su importancia, veamos un ejemplo práctico para entender mejor cómo funciona.

Supongamos que tenemos los siguientes datos del resultado económico de una empresa en millones de dólares para los últimos cinco años: 8, 12, 6, -4, 10. Queremos calcular la varianza de este conjunto de datos utilizando la fórmula que mencionamos anteriormente.

Paso 1: Calcular la media aritmética

Primero, calculamos la media aritmética de los datos sumándolos y dividiendo entre el número total de datos (en este caso, 5):

Media aritmética (X̄) = (8 + 12 + 6 – 4 + 10) ÷ 5 = 6,4 millones de dólares

Paso 2: Utilizar la fórmula de la varianza

A continuación, utilizamos la fórmula de la varianza para calcular el cuadrado de las diferencias entre cada dato y la media aritmética, y luego sumarlos:

Donde x_i es cada dato, X̄ es la media aritmética y n es el número total de datos.

Sustituimos los datos y la media aritmética en la fórmula de la varianza:

Varianza (Var(X)) = [(8 – 6,4)² + (12 – 6,4)² + (6 – 6,4)² + (-4 – 6,4)² + (10 – 6,4)²] ÷ (5 – 1)

Paso 3: Resolver las operaciones

Ahora resolvemos las operaciones para obtener el valor de la varianza:

Varianza (Var(X)) = [1,6² + 5,6² + 0,16² + (-10,4)² + 3,6²] ÷ 4

Varianza (Var(X)) = [2,56 + 31,36 + 0,0256 + 108,16 + 12,96] ÷ 4

Varianza (Var(X)) = 155,072 ÷ 4

Varianza (Var(X)) = 38,768 millones de dólares al cuadrado

La varianza de este conjunto de datos es de 38,768 millones de dólares al cuadrado, lo cual nos da una medida de la dispersión o variabilidad de los datos en relación con la media aritmética.

La frecuencia relativa es un concepto estadístico que te permite expresar la proporción o porcentaje de un evento o valor específico en relación con el total de observaciones o datos disponibles. Es una medida que te permite entender la proporción de un valor en comparación con el conjunto completo de datos.

Por ejemplo, si estás analizando la distribución de género en una muestra de 100 personas y encuentras que hay 60 mujeres y 40 hombres, la frecuencia relativa del género femenino sería 60% y la del género masculino sería 40%. Esto te dará una idea clara de la proporción de cada género en la muestra.

¿Qué nos indica la frecuencia relativa?

La frecuencia relativa te brinda una medida relativa de la importancia o prevalencia de un evento o valor en un conjunto de datos. Por ejemplo, si tienes datos sobre la cantidad de estudiantes que aprueban un examen en una clase, la frecuencia relativa te dará la proporción de estudiantes que aprobaron en comparación con el total de estudiantes evaluados.

En resumen, la frecuencia relativa es una medida estadística que te permite expresar la proporción o porcentaje de un evento o valor específico en relación con el total de observaciones o datos disponibles. Es una herramienta útil para comprender la importancia relativa de diferentes eventos o valores en un conjunto de datos y se expresa como un porcentaje que suma 100%.

¿Cómo se calcula la frecuencia relativa?

En realidad, no es tan complejo el proceso para calcular la frecuencia relativa. Por ello, te lo explicamos de la forma más simple en los siguientes párrafos.

Para calcular la frecuencia relativa, tienes que empezar dividiendo la frecuencia absoluta entre el valor total de observaciones.

Luego, multiplicar el resultado por 100 para expresarlo como porcentaje. La fórmula para realizar el cálculo de frecuencia relativa es esta:

Frecuencia Relativa = (Frecuencia Absoluta del evento ÷ valor específico) ÷ (Total de observaciones o datos) · 100

Ahora bien, para entender un poco mejor este proceso, revisemos el siguiente ejemplo práctico:

Supongamos que tienes un conjunto de datos con información sobre la cantidad de horas de estudio diarias de un grupo de estudiantes. Los datos son los siguientes:

• Estudiante 1: 3 horas
• Estudiante 2: 4 horas
• Estudiante 3: 2 horas
• Estudiante 4: 5 horas
• Estudiante 5: 3 horas

En este caso, el evento o valor específico que queremos calcular es la cantidad de horas de estudio diarias. El total de observaciones o datos disponibles es 5, ya que hay 5 estudiantes en el conjunto de datos.

Paso 1: Calcular la Frecuencia Absoluta

Primero, necesitamos calcular la frecuencia absoluta, que es la cantidad de veces que ocurre el evento o valor específico en el conjunto de datos. En este caso, tenemos las siguientes frecuencias absolutas para cada cantidad de horas de estudio diarias:

• 3 horas: 2 estudiantes
• 4 horas: 1 estudiante
• 2 horas: 1 estudiante
• 5 horas: 1 estudiante

Paso 2: Calcular la Frecuencia Relativa

A continuación, vamos a calcular la frecuencia relativa dividiendo la frecuencia absoluta de cada cantidad de horas de estudio diarias entre el total de observaciones o datos disponibles (5). Posteriormente, se procede con la multiplicación del resultado por 100 para que se exprese luego como un porcentaje.

Frecuencia Relativa de 3 horas = (Frecuencia Absoluta de 3 horas ÷ Total de observaciones) · 100

= (2 ÷ 5) · 100 = 40%

Frecuencia Relativa de 4 horas = (Frecuencia Absoluta de 4 horas ÷ Total de observaciones) · 100

= (1 ÷ 5) · 100 = 20%

Frecuencia Relativa de 2 horas = (Frecuencia Absoluta de 2 horas ÷ Total de observaciones) · 100

= (1 ÷ 5) · 100 = 20%

Frecuencia Relativa de 5 horas = (Frecuencia Absoluta de 5 horas ÷ Total de observaciones) · 100

= (1 ÷ 5) · 100 = 20%

Entonces, la frecuencia relativa de cada cantidad de horas de estudio diarias en este conjunto de datos sería: 40% para 3 horas, 20% para 4 horas, 20% para 2 horas y 20% para 5 horas.

¿Cómo se representa la frecuencia relativa?

La frecuencia relativa se representa como un porcentaje y nos muestra la proporción de veces que ocurre un evento específico en relación con el total de observaciones. Es una forma de expresar la frecuencia en términos relativos en lugar de absolutos.

La representación de la frecuencia relativa puede ser a través de gráficos de barras, gráficos circulares o tablas con porcentajes. Esto nos permite visualizar de manera clara y concisa la proporción de cada evento en el conjunto de datos, lo que facilita la interpretación de los resultados y la comparación entre diferentes eventos.

¿Cuál es la diferencia entre frecuencia relativa y frecuencia absoluta?

La frecuencia relativa es el porcentaje o proporción de veces que ocurre un evento específico en relación con el total de eventos, mientras que la frecuencia absoluta es simplemente el número total de veces que ocurre un evento específico. En resumen, la frecuencia relativa se expresa en porcentaje, mientras que la frecuencia absoluta se expresa en números.

¿Cuáles son las aplicaciones de la frecuencia relativa?

La frecuencia relativa es una herramienta poderosa en muchas áreas. Por ejemplo, en estadística, se utiliza para calcular probabilidades y hacer predicciones basadas en datos observados.

También se aplica en estudios de mercado para analizar preferencias de los consumidores. Además, en la investigación científica, se emplea para determinar la prevalencia de ciertos fenómenos en una muestra estadística.

En general, la frecuencia relativa te permite obtener una visión clara y cuantitativa de la probabilidad de que ocurra un evento en relación con el total de eventos observados.

¿Cómo se relaciona la frecuencia relativa con los intervalos matemáticos?

Los intervalos matemáticos son una forma de representar la frecuencia relativa en un rango específico. Por ejemplo, puedes dividir datos en rangos y calcular la frecuencia relativa para cada intervalo.

Esto te permite obtener una visión más detallada y comprensible de la distribución de datos en diferentes categorías o grupos. Los intervalos matemáticos son una herramienta valiosa para analizar datos y visualizar patrones o tendencias en un conjunto de datos.

Te ayudan a obtener una representación clara y resumida de la frecuencia relativa en diferentes rangos, lo que puede ser útil en el análisis de datos y la toma de decisiones basada en datos.

Ejemplos de frecuencia relativa

Ahora que comprendemos mejor de qué se trata la frecuencia relativa, podemos mostrarte algunos ejemplos simples para entender mejor su funcionamiento.

Ejemplo 1: Temperaturas de un mes en grados Celsius

Supongamos que tienes datos de las temperaturas diarias de un mes en grados Celsius y deseas calcular la frecuencia relativa utilizando intervalos de 5 grados Celsius. Los datos son los siguientes:

12, 15, 17, 18, 20, 22, 23, 25, 26, 27, 29, 30, 32, 33, 34, 35, 36, 38, 40, 42, 44, 45, 47, 49, 50

Paso 1: Definir los intervalos matemáticos:

En este caso, usaremos intervalos de 5 grados Celsius. El primer intervalo será de 10 a 14 (10-14), el segundo de 15 a 19 (15-19), y así sucesivamente.

Paso 2: Contar la frecuencia absoluta:

Para cada intervalo, cuentas la cantidad de datos que caen dentro de ese rango. Por ejemplo, en el primer intervalo (10-14), hay 1 dato que está dentro de ese rango.

Paso 3: Calcular la frecuencia relativa:

Divides la frecuencia absoluta de cada intervalo entre el total de datos (en este caso, 26) y lo multiplicas por 100 para obtener el porcentaje. Por ejemplo, en el primer intervalo (10-14), la frecuencia absoluta es 1, y la frecuencia relativa es (1÷26) · 100 ≈ 3,85%.

Paso 4: Repetir el proceso para los demás intervalos:

Realizas el mismo proceso de contar la frecuencia absoluta y calcular la frecuencia relativa para los demás intervalos.

Ejemplo 2: Ingresos mensuales en dólares

Supongamos que tienes datos de los ingresos mensuales de un grupo de personas en dólares y deseas calcular la frecuencia relativa utilizando intervalos de 1000 dólares. Los datos son los siguientes:

1500, 1800, 2000, 2200, 2500, 2700, 2900, 3000, 3200, 3500, 3800, 4000, 4200, 4500, 4700, 5000, 5200, 5500, 5800, 6000, 6200, 6500, 6700, 7000

Paso 1: Definir los intervalos matemáticos:

En este caso, usaremos intervalos de 1000 dólares. El primer intervalo será de 1000 a 1999 (1000-1999), el segundo de 2000 a 2999 (2000-2999), y así sucesivamente.

Paso 2: Contar la frecuencia absoluta:

Para cada intervalo, cuentas la cantidad de datos que caen dentro de ese rango. Por ejemplo, en el primer intervalo (1000-1999), hay 3 personas cuyos ingresos mensuales están dentro de ese rango.

Paso 3: Calcular la frecuencia relativa:

Divides la frecuencia absoluta de cada intervalo entre el total de datos (en este caso, 24) y lo multiplicas por 100 para obtener el porcentaje. Por ejemplo, en el primer intervalo (1000-1999), la frecuencia absoluta es 3, y la frecuencia relativa es (3÷24) · 100 ≈ 12,50%.

Paso 4: Repetir el proceso para los demás intervalos:

Realizas el mismo proceso de contar la frecuencia absoluta y calcular la frecuencia relativa para los demás intervalos.

La frecuencia absoluta (fi) es la cantidad de veces que aparece un dato o valor en un conjunto de datos. Es simplemente contar cuántas veces ocurre algo. Por ejemplo, si tienes un conjunto de datos con las edades de tus amigos y la edad de 20 años aparece 5 veces, entonces la frecuencia absoluta de 20 años es 5.

En otras palabras, una forma simple y directa de contar cuántas veces algo sucede en un conjunto de datos. La frecuencia absoluta se utiliza para obtener una visión clara de la distribución de datos y entender qué valores son más comunes. En general, es como un conteo básico, pero muy útil para analizar datos.

¿Qué nos indica la frecuencia absoluta?

La frecuencia absoluta nos indica cuántas veces ocurre un valor específico en un conjunto de datos. En este sentido, cabe mencionar que, es una medida simple pero poderosa para entender la distribución de datos.

Con la frecuencia absoluta, puedes identificar rápidamente los valores más comunes y entender la tendencia de los datos. Además, puedes usar la frecuencia absoluta para calcular otras medidas estadísticas, como la moda, que es el valor con la mayor frecuencia absoluta.

En resumen, la frecuencia absoluta es una herramienta importante para analizar y comprender los datos de una manera sencilla y efectiva. Aunque muy pocas personas la entienden, te permite obtener información valiosa sobre la distribución de los datos en un abrir y cerrar de ojos.

¿Cómo se calcula la frecuencia absoluta?

Al contrario de lo que puedes creer, calcular la frecuencia absoluta no es nada fuera de lo normal, de hecho, resulta bastante sencillo. Para encontrar la frecuencia absoluta, simplemente cuenta cuántas veces aparece un valor específico en un conjunto de datos.

Por ejemplo, si tienes una lista de edades y quieres saber cuántas veces aparece la edad de 20 años, cuenta cuántas veces se repite ese valor en la lista. Esa cantidad es la frecuencia absoluta de 20 años en tus datos. Puedes hacerlo manualmente o con herramientas de software, como hojas de cálculo o programas estadísticos.

La fórmula es básicamente contar y registrar el número de veces que un valor ocurre en tus datos. La frecuencia absoluta te da una visión clara de cuántas veces ocurre algo y es una forma simple pero esencial de analizar datos en estadística. Es fácil de hacer y te brinda información valiosa sobre tus datos. Veamos un ejemplo, para entender de mejor forma:

Imagina que tienes una lista de edades de tus amigos: 22, 20, 18, 20, 21, 22, 19, 20, 20, 21. Quieres calcular la frecuencia absoluta de la edad de 20 años en este conjunto de datos.

• Paso 1: Observa el valor que deseas analizar, en este caso, 20 años.
• Paso 2: Cuenta cuántas veces aparece ese valor en la lista. En este caso, el valor de 20 años aparece 4 veces en la lista.
• Paso 3: Registra la cantidad obtenida como la frecuencia absoluta del valor de interés. En este ejemplo, la frecuencia absoluta de 20 años es 4.

Así de simple es calcular la frecuencia absoluta. Puedes aplicar el mismo proceso para otros valores en la lista y obtener la frecuencia absoluta de cada uno. Esta medida te ayuda a entender cuántas veces aparece cada valor y proporciona una visión clara de la distribución de datos en tu conjunto de datos.

¿Cómo se representa la frecuencia absoluta?

La frecuencia absoluta se puede representar de diferentes maneras para visualizar la distribución de datos. Puedes usar gráficos de barras, tablas o diagramas de dispersión. Por ejemplo, si estás analizando las edades de tus amigos, puedes crear un gráfico de barras donde el eje vertical representa la frecuencia absoluta de cada edad y el eje horizontal muestra los diferentes valores de edad.

Cada barra representará la frecuencia absoluta de un valor específico. También puedes crear una tabla donde listas los valores y sus correspondientes frecuencias absolutas. Otra opción es usar un diagrama de dispersión, donde los puntos en el gráfico representan los valores y su posición en el eje vertical muestra la frecuencia absoluta.

Estas representaciones visuales te permiten tener una imagen clara y comprensible de la distribución de datos, lo que facilita la interpretación de los resultados.

¿Cuál es la diferencia entre frecuencia absoluta y frecuencia relativa?

La diferencia entre la frecuencia absoluta y la frecuencia relativa radica en cómo se expresan los datos. La frecuencia absoluta es simplemente el recuento de cuántas veces aparece un valor específico en un conjunto de datos. Por otro lado, la frecuencia relativa se refiere a la proporción o porcentaje que representa la frecuencia absoluta en relación con el tamaño total del conjunto de datos.

Por ejemplo, si tienes una lista de edades de tus amigos y la frecuencia absoluta de la edad de 20 años es 4, significa que el valor de 20 años aparece 4 veces en tu lista. Sin embargo, la frecuencia relativa de la edad de 20 años dependerá del tamaño total de tu lista. Si tienes un total de 50 edades en tu lista, entonces la frecuencia relativa de la edad de 20 años será 4÷50, que es igual al 8% o 0,08 en forma decimal.

La frecuencia relativa es una medida que proporciona información sobre la proporción de un valor específico en relación con el conjunto de datos completo. Por otra parte, la frecuencia absoluta simplemente cuenta cuántas veces aparece un valor sin tener en cuenta la proporción en relación con el conjunto de datos completo.

¿Cuáles son las aplicaciones de la frecuencia absoluta?

La frecuencia absoluta tiene diversas aplicaciones en diferentes campos. Algunas de las aplicaciones más comunes son:

Estadísticas

En estadística, la frecuencia absoluta se utiliza para describir y resumir datos en forma de conteo o cantidad. Se puede usar para calcular medidas de tendencia central, como la moda, y para generar gráficos y representaciones visuales de datos, como histogramas.

Investigación de mercado

En este contexto, la frecuencia absoluta se puede utilizar para analizar datos demográficos, preferencias del consumidor, comportamientos de compra, entre otros. Esto permite a las empresas entender mejor a su audiencia y tomar decisiones informadas en la planificación de estrategias de marketing.

Ciencias sociales

En disciplinas como la sociología, psicología y ciencia política, la frecuencia absoluta se utiliza para analizar datos cualitativos y cuantitativos en investigaciones sobre comportamiento humano, actitudes, opiniones y otros aspectos relacionados con las ciencias sociales.

Ciencias de la salud

Por otro lado, en la medicina y otras ciencias de la salud, la frecuencia absoluta se utiliza para analizar datos epidemiológicos, como la incidencia de enfermedades, la prevalencia de factores de riesgo, la distribución de síntomas y otros indicadores de salud de una población.

Como viste antes, la frecuencia absoluta tiene un campo de aplicación bastante amplio que le permite ser útil de muchas formas. Por ello, es esencial conocer bien de qué se trata.

¿Qué relación hay entre la frecuencia absoluta y los intervalos matemáticos?

La relación entre la frecuencia absoluta y los intervalos matemáticos radica en cómo se agrupan los datos en intervalos o rangos para el cálculo de la frecuencia absoluta en estadística.

Los intervalos matemáticos son rangos de valores que se definen previamente y se utilizan para agrupar los datos en categorías o clases. La frecuencia absoluta se refiere al conteo o cantidad de observaciones que caen dentro de cada intervalo o clase.

En otras palabras, cuando se trabaja con datos continuos o variables que tienen un rango amplio de valores, puede ser más conveniente y práctico agruparlos en intervalos matemáticos para facilitar su análisis y presentación. La frecuencia absoluta se obtiene al contar el número de observaciones que caen dentro de cada intervalo o rango específico.

Por ejemplo, supongamos que se tiene un conjunto de datos de edades de una muestra de personas, que van desde 18 hasta 80 años. Si se decide agrupar los datos en intervalos de 10 años, los intervalos matemáticos serían: 18-28, 29-39, 40-50, 51-61, 62-72 y 73-83.

Ejemplos de frecuencia absoluta

Ahora que tenemos claro qué es la frecuencia absoluta, veamos algunos ejemplos prácticos para comprender un poco mejor su función e importancia.

Ejemplo 1: Edades de una muestra de estudiantes

Supongamos que se tiene una muestra de edades de 100 estudiantes y se decide agrupar los datos en intervalos de 5 años. Los intervalos matemáticos serían: 10-14, 15-19, 20-24, 25-29, etc. La frecuencia absoluta se obtendría contando el número de estudiantes que caen dentro de cada uno de estos intervalos, por ejemplo:

• Intervalo 10-14: 12 estudiantes
• Intervalo 15-19: 28 estudiantes
• Intervalo 20-24: 30 estudiantes
• Intervalo 25-29: 18 estudiantes

Y así sucesivamente para cada intervalo. La frecuencia absoluta en este caso representa la cantidad de estudiantes en cada rango de edades.

Ejemplo 2: Ingresos anuales de una empresa

Supongamos que se tiene una empresa y se desea analizar los ingresos anuales de los empleados. Se decide agrupar los ingresos en intervalos de 10.000 dólares. Los intervalos matemáticos serían: 0-10,000, 10,001-20,000, 20,001-30,000, etc. La frecuencia absoluta se obtendría contando el número de empleados cuyos ingresos caen dentro de cada intervalo, por ejemplo:

• Intervalo 0-10,000: 15 empleados
• Intervalo 10,001-20,000: 22 empleados
• Intervalo 20,001-30,000: 12 empleados

Y así sucesivamente para cada intervalo. La frecuencia absoluta en este caso representa la cantidad de empleados que tienen ingresos en cada rango específico.

Estos son solo dos ejemplos de cómo se puede utilizar la frecuencia absoluta con intervalos matemáticos en diferentes contextos. Es importante recordar que los intervalos matemáticos pueden variar dependiendo del contexto y del objetivo del análisis.

La desviación típica o estándar es una medida estadística que indica cuánto se alejan los datos individuales de la media o promedio de un conjunto de datos. Es una medida de dispersión que se utiliza para entender cuánto varían los datos en relación con la media del conjunto.

En palabras más complejas, la desviación típica o estándar es la raíz cuadrada de la varianza. La varianza se calcula como el promedio de las diferencias al cuadrado entre cada dato y la media del conjunto. Al tomar la raíz cuadrada de la varianza, se obtiene la desviación típica, que está en las mismas unidades que los datos originales.

Cabe mencionar que, es una medida importante en estadística. Gracias a ella, es posible cuantificar la dispersión de los datos y entender cómo se distribuyen en relación con la media. Una desviación típica baja indica que los datos tienden a estar cerca de la media. Por otro lado, una desviación típica alta indica que los datos están más dispersos o alejados de la media.

En general, la desviación típica se utiliza para entender la variabilidad de los datos en un conjunto y para realizar comparaciones.

¿Para qué sirve la desviación típica?

La desviación típica es una herramienta estadística que tiene varias aplicaciones en el análisis de datos. Algunas de las utilidades más conocidas son las siguientes:

• Medida de dispersión: permite cuantificar cuánto se alejan los datos individuales de la media o promedio del conjunto. Una desviación típica alta indica una mayor dispersión o variabilidad de los datos, mientras que una desviación típica baja indica una menor dispersión.
• Comparación de conjuntos de datos: se puede usar para comparar la variabilidad entre diferentes conjuntos de datos. Un conjunto con una desviación típica mayor tendrá datos más dispersos que uno con una desviación típica menor.
• Identificación de valores atípicos: también puede ayudar a identificar valores atípicos o extremos en un conjunto de datos. Si un dato se encuentra a varias desviaciones típicas de la media, puede indicar que es un valor inusual o atípico.
• Evaluación de la precisión de un modelo: en algunos casos, la desviación típica se emplea como medida de la precisión de un modelo o estimación. Por ejemplo, en estadística inferencial, se puede utilizar la desviación típica para calcular intervalos de confianza o realizar pruebas de hipótesis.

Propiedades de la desviación típica

La desviación típica tiene varias propiedades importantes que vale la pena mencionar:

• La desviación típica es una medida de distancia, por lo que siempre es un valor no negativo.
• Si todos los datos en el conjunto tienen el mismo valor, la desviación típica será igual a cero.
• Es afectada por los valores atípicos y puede ser influenciada significativamente en el conjunto de datos.
• Es sensible a la escala de los datos. Si los datos están en una escala grande, la desviación típica también será grande y viceversa.
• Es una medida de dispersión relativa, ya que se expresa en las mismas unidades que los datos originales.

¿Cuál es la fórmula de la desviación típica?

La fórmula matemática de la desviación típica es la siguiente:

Donde:

σ: Representa la desviación típica.

Σ: Indica la suma.

xi: Son los valores individuales del conjunto de datos.

media: Es la media o promedio del conjunto de datos.

n: Es el número total de datos en el conjunto.

La desviación típica es una medida de dispersión que nos permite entender cuánto se alejan los datos de un conjunto en relación con su media o promedio. Se obtiene mediante el cálculo de la raíz cuadrada de la suma de los cuadrados de las diferencias entre cada valor del conjunto y la media del conjunto, dividido por el número total de datos en el conjunto.

¿Cómo se calcula la desviación típica?

La desviación típica se calcula siguiendo los siguientes pasos:

1. Calcular la media o promedio del conjunto de datos

La media se obtiene con la suma todos los valores del conjunto de datos y la división del resultado entre el valor total de datos. Matemáticamente se expresa como:

Donde xi es cada uno de los valores del conjunto de datos, n es el número de datos en el conjunto y Σ representa la suma.

2. Restar la media a cada uno de los valores del conjunto de datos

Para obtener las diferencias entre cada valor del conjunto de datos y la media, se resta la media (calculada en el paso anterior) a cada uno de los valores del conjunto de datos. Esto permite identificar cuánto se alejan los datos de la media.

3. Elevar al cuadrado cada una de las diferencias obtenidas en el paso anterior

Las diferencias obtenidas en el paso anterior se elevan al cuadrado. Este paso se realiza para evitar que las diferencias positivas y negativas se anulen entre sí y para enfatizar los valores que están más lejos de la media.

4. Calcular el promedio de los valores obtenidos en el paso anterior

Se calcula el promedio de los valores obtenidos en el paso anterior. Este promedio representa la suma de los cuadrados de las diferencias dividida entre el número total de datos. Matemáticamente se expresa como:

Promedio de los cuadrados de las diferencias = Σ((xi – media)²) ÷ n

5. Obtener la raíz cuadrada del valor obtenido en el paso anterior

El último paso es obtener la raíz cuadrada del valor obtenido en el paso anterior. Esto proporciona la desviación típica, que es una medida de dispersión de los datos en relación con la media.

¿Cómo se interpreta la desviación típica?

Es importante tener en cuenta que la interpretación de la desviación típica depende del contexto y de la naturaleza de los datos en estudio.

Por lo tanto, es fundamental comprender adecuadamente el significado de la desviación típica y utilizarla en conjunto con otras medidas estadísticas para obtener una comprensión completa y precisa de la variabilidad de los datos. Veamos algunos ejemplos, a continuación.

Análisis de la variabilidad

La desviación típica permite evaluar la variabilidad o dispersión de los datos en un conjunto. Si la desviación típica es baja, indica que los datos están cercanos a la media y tienen poca variabilidad. Por otro lado, si la desviación típica es alta, indica que los datos están más dispersos y presentan mayor variabilidad.

Comparación de datos

Es útil para comparar la variabilidad entre diferentes conjuntos de datos. Por ejemplo, si se compara la desviación típica de los ingresos de dos países, se puede inferir cuál tiene una mayor variabilidad en los ingresos de su población.

Identificación de valores atípicos

Ayuda a identificar valores atípicos o datos inusuales en un conjunto. Los datos que se encuentren a una distancia mayor a 1 o 2 desviaciones típicas de la media pueden ser considerados como valores atípicos.

Evaluación de la precisión de la medida

También se utiliza como una medida de la precisión o confiabilidad de una medida o estimación. Por ejemplo, si se está realizando una investigación y se obtienen mediciones con una alta desviación típica, puede indicar que las mediciones son menos precisas y que se requiere un mayor cuidado en la recolección de datos.

Evaluación de la normalidad de los datos

La desviación típica se usa en conjunto con otras medidas para evaluar si los datos siguen una distribución normal. Si los datos tienen una desviación típica baja en comparación con la media, puede indicar que los datos están distribuidos de manera aproximada a una distribución normal.

Ejemplos numéricos de desviación típica

Si bien es cierto que, en líneas generales, puede resultar compleja, la desviación típica se entiende de forma simple. Para aclarar dudas, compartimos algunos ejemplos, a continuación, empleando dos métodos distintos.

Raíz cuadrada de la varianza

Supongamos que tenemos los siguientes datos: 9, 3, 8, 9 y 16.

Paso 1: Calcular la media aritmética:

Media aritmética = (9 + 3 + 8 + 9 + 16) ÷ 5 = 9.

Paso 2: Aplicar la fórmula de la varianza:

Varianza = [(9 – 9)² + (3 – 9)² + (8 – 9)² + (9 – 9)² + (16 – 9)²] ÷ 5 = 86 ÷ 5 = 17,2.

Paso 3: Tomar la raíz cuadrada de la varianza:

Desviación típica = √(17,2) ≈ 4,14.

Suma de las desviaciones y dividir entre el total de observaciones

Supongamos que tenemos los siguientes datos: 2, 4, 2, 4, 2 y 4.

Paso 1: Calcular la media aritmética:

Media aritmética = (2 + 4 + 2 + 4 + 2 + 4) ÷ 6 = 3.

Paso 2: Calcular la desviación típica sumando las desviaciones y dividiendo entre el número total de observaciones:

Desviación típica = [(2 – 3) + (4 – 3) + (2 – 3) + (4 – 3) + (2 – 3) + (4 – 3)] ÷ 6 = (1 + 1 + 1 + 1 + 1 + 1) ÷ 6 = 1.

En ambos casos, obtenemos una desviación típica de aproximadamente 4,14 y 1 respectivamente, utilizando diferentes métodos de cálculo. Esto ilustra cómo se puede obtener la desviación típica usando la raíz cuadrada de la varianza o sumando las desviaciones y dividiendo entre el número total de observaciones.

Los percentiles son medidas estadísticas utilizadas para interpretar datos y entender la posición relativa de un valor dentro de una distribución. Son una forma común de resumir y analizar grandes conjuntos de datos.

Cuando se habla de percentiles, se está hablando de cómo un valor específico se compara con el resto de los datos. El percentil 50, por ejemplo, divide a los datos en dos partes iguales: el 50% de los datos está por debajo y el otro 50% está por encima.

Generalmente, el percentil se emplea para entender cómo se distribuyen los datos en un conjunto. Por ejemplo, el percentil 25, marca el punto en el que el 25% de los datos está por debajo y el 75% está por encima.

Además, cabe mencionar que, los percentiles se usan también para evaluar la posición relativa de un valor en comparación con otros valores. Por ejemplo, si tu puntuación en un examen está en el percentil 90, significa que obtuviste una puntuación mejor que el 90% de los otros participantes.

¿Cómo se calculan los percentiles?

Calcular los percentiles implica ordenar un conjunto de datos y determinar el valor que se encuentra en una posición específica en relación con el total de datos. Veamos, a continuación, la forma correcta de calcular un percentil.

1. Ordena los datos: primero, ordena los datos de manera ascendente o descendente, dependiendo del percentil que deseas calcular. Es importante tener los datos organizados para poder identificar la posición relativa del valor deseado.

2. Identifica la posición del percentil: luego, determina la posición relativa del percentil que deseas calcular en relación con el total de datos. Esto se puede hacer mediante la fórmula:

Posición del percentil = (Percentil deseado ÷ 100) · (n + 1)

Donde “Percentil deseado” es el valor del percentil que deseas calcular y “n” es el total de datos en el conjunto ordenado.

3. Encuentra el valor del percentil: usando la posición del percentil calculada en el paso anterior, encuentra el valor correspondiente en el conjunto ordenado de datos. Si la posición del percentil es un número entero, entonces el valor en esa posición es el percentil buscado. Si la posición del percentil no es un número entero, puedes interpolar entre los dos valores más cercanos en la posición inferior y superior para obtener una estimación del percentil.

Ten en cuenta que hay diferentes métodos para calcular los percentiles, como el método de interpolación lineal, el método de interpolación vecino más cercano, entre otros. La elección del método afecta ligeramente los resultados, por lo que es importante ser consistente y utilizar el mismo método en todos los cálculos.

¿Cuál es la importancia de los percentiles en la interpretación de datos?

Los percentiles son una herramienta fundamental en la interpretación de datos porque proporcionan una forma estadística de comprender la posición relativa de un valor dentro de un conjunto de datos. Veamos algunos puntos clave sobre la importancia de los percentiles en la interpretación de datos:

Medida de posición

En primer lugar, permiten determinar la posición relativa de un valor dentro de un conjunto de datos. Por ejemplo, el percentil 50, conocido como la mediana, indica el valor que se encuentra en el centro del conjunto de datos, dividiéndolo en dos partes iguales.

Los percentiles más altos, como el 75 o el 90, indican el valor por encima del cual se encuentra un determinado porcentaje de los datos, lo que ayuda a entender la distribución y dispersión de los datos.

Comparación de datos

El uso de percentiles sirve para comparar valores en diferentes conjuntos de datos o en diferentes momentos en el tiempo. Por ejemplo, al comparar los percentiles de ingresos de diferentes grupos poblacionales, se puede determinar cómo se distribuyen los ingresos en cada grupo y si hay desigualdades económicas.

Además, al calcular los percentiles en diferentes momentos en el tiempo, se puede analizar la evolución o cambios en la distribución de los datos a lo largo del tiempo.

Identificación de valores atípicos

También son útiles para identificar valores atípicos u «outliers» en un conjunto de datos. Por ejemplo, si un valor se encuentra por encima del percentil 95, indica que está por encima del 95% de los datos en el conjunto, lo que podría ser considerado como un valor inusual o atípico.

Esto puede ser relevante en análisis de datos para identificar valores extremos o datos anómalos que puedan afectar la interpretación de los resultados.

¿Cuál es el rango de valores posibles para un percentil?

El rango de valores posibles para un percentil es de 0 a 100. Los percentiles representan la posición relativa de un valor dentro de un conjunto de datos, expresada como un porcentaje.

Por lo tanto, un percentil puede variar desde el 0, que representa el valor más bajo en el conjunto de datos, hasta el 100, que representa el valor más alto en el conjunto de datos.

Por ejemplo, el percentil 50, también conocido como la mediana, representa el valor que se encuentra en el centro del conjunto de datos, dividiendo los datos en dos partes iguales. Un valor que se encuentra en el percentil 50 significa que está por encima del 50% de los datos y por debajo del 50% de los datos en el conjunto.

De manera similar, el percentil 75 representa el valor por encima del cual se encuentra el 75% de los datos, y el percentil 90 representa el valor por encima del cual se encuentra el 90% de los datos.

Los percentiles no tienen un límite, ya que están basados en un porcentaje relativo a los datos en el conjunto. Esto significa que cualquier valor en el conjunto de datos, puede ser representado por un percentil. Sin embargo, esto depende de su posición relativa dentro del conjunto.

¿Cuál es la diferencia entre un percentil y una mediana?

La mediana es un valor específico que divide un conjunto de datos en dos partes iguales, con el 50% de los datos por encima y el 50% por debajo. El percentil es una medida que indica la posición relativa de un valor en un conjunto de datos, expresada como un porcentaje.

Por ejemplo, el percentil 50 es equivalente a la mediana. La diferencia radica en que la mediana es un valor específico, mientras que los percentiles son una medida más generalizada en términos de porcentaje.

Los percentiles son útiles para evaluar la posición relativa de un valor en el conjunto completo de datos, mientras que la mediana es simplemente un valor específico en la posición central del conjunto de datos.

¿Cuáles son algunas consideraciones al usar percentiles en el análisis de datos?

Al utilizar percentiles en el análisis de datos, es importante tener en cuenta algunas limitaciones y consideraciones clave:

• Representación limitada de los datos: capturan solo un porcentaje específico de los datos, lo que implica que no reflejan la distribución completa de los valores.
• Sensibilidad a datos extremos: los percentiles pueden verse influenciados por valores atípicos o datos extremos en el conjunto de datos, lo que puede sesgar su interpretación.
• Falta de información sobre la variabilidad de los datos: no proporcionan detalles sobre la variabilidad o dispersión de los datos en un conjunto, lo cual puede ser importante para entender la distribución completa de los datos.
• Dependencia del tamaño de muestra: el tamaño de la muestra estadística del conjunto de datos puede afectar los percentiles, con muestras pequeñas que pueden tener percentiles más fluctuantes y menos precisos.
• Interpretación adecuada: es fundamental no hacer supuestos erróneos basados únicamente en los percentiles, sino considerarlos en conjunto con otras medidas descriptivas y el contexto específico del análisis de datos.

Ejemplos numéricos para calcular percentiles

Llegado a este punto, es posible que tengas dudas sobre cómo hacer el cálculo de percentiles. Por ello, te compartimos algunos ejemplos numéricos que puedes tener en cuenta.

Ejemplo 1: Percentil 75

Para calcular el percentil 75, primero ordenamos los datos de menor a mayor: 10, 12, 15, 18, 20, 22, 25, 28, 30, 32.

Luego, multiplicamos el percentil deseado (75) por el total de datos (10) y dividimos entre 100 para obtener la posición aproximada del percentil en el conjunto de datos: (75 · 10) ÷ 100 = 7,5. Como 7,5 no es un número entero, tomamos el valor que se encuentra en la posición inmediatamente superior (en este caso, el octavo valor), que es 28. Por lo tanto, el percentil 75 es igual a 28.

Ejemplo 2: Percentil 90

Utilizando los mismos datos del ejemplo anterior, para calcular el percentil 90, multiplicamos el percentil deseado (90) por el total de datos (10) y dividimos por 100: (90 · 10) ÷ 100 = 9.

Como 9 es un número entero, tomamos el valor que se encuentra en la novena posición (en este caso, el valor más alto del conjunto de datos), que es 32. Por lo tanto, el percentil 90 es igual a 32.

La dispersión estadística es un concepto amplio que se refiere a la variabilidad o diferencias que pueden existir en un conjunto de datos. En estadística, se utiliza para describir cuán lejos están los datos individuales de un conjunto de valores centrales, como la media o la mediana.

Existen varios tipos de medidas de dispersión estadística. En primer lugar, tenemos la desviación estándar y el rango. Además, la varianza, la amplitud intercuartil y el coeficiente de variación. Cada una de estas medidas proporciona una forma diferente de medir la variabilidad de los datos.

La dispersión estadística es importante porque puede dar información valiosa sobre la distribución de los datos y ayuda a detectar valores atípicos o anomalías en los datos. Además, la dispersión estadística es útil en la toma de decisiones y en la evaluación de riesgos en una variedad de campos, desde la investigación científica hasta la gestión empresarial.

¿Cuáles son los tipos de medidas de dispersión estadística?

La dispersión estadística se utiliza para medir la variabilidad o la distancia que existe entre los valores de un conjunto de datos. Hay varias formas de estudiar la dispersión estadística, pero aquí te presento algunas técnicas comunes:

• Rango: el rango es la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos. Esta medida es fácil de calcular, pero puede verse afectada por valores extremos o atípicos.
• Desviación estándar: es una medida de dispersión que se calcula como la raíz cuadrada de la varianza. La varianza mide la distancia promedio de cada punto de datos con respecto a la media. La desviación estándar es una medida más precisa que el rango, pero también se ve afectada por valores atípicos.
• Coeficiente de variación: medida de la dispersión relativa de un conjunto de datos. Se calcula dividiendo la desviación estándar por la media y multiplicando el resultado por 100%. Esta medida es útil para comparar la variabilidad de dos o más conjuntos de datos que tienen diferentes escalas o unidades de medida.
• Diagramas de caja y bigotes: gráficos que muestran la distribución y la dispersión de un conjunto de datos. La caja representa el rango intercuartil (IQR) y los bigotes muestran el rango máximo y mínimo de los datos. Este gráfico es útil para identificar valores atípicos y para comparar la variabilidad de dos o más conjuntos de datos.

¿Para qué sirve la dispersión estadística?

Al estudiar la dispersión estadística de un conjunto de datos, se pueden obtener varias ventajas, entre ellas:

• Identificar valores atípicos: ayuda a identificar valores atípicos o inusuales en un conjunto de datos. Esto puede ser importante para descubrir errores en la medición o en la recopilación de datos, o para identificar observaciones que son significativamente diferentes del resto de los datos.
• Evaluar la consistencia de los datos: es útil para evaluar la consistencia de los datos. Si un conjunto de datos tiene una gran dispersión, puede ser una señal de que los datos no son muy precisos o que hay mucha variación en las condiciones de medición.
• Comparar conjuntos de datos: sirve para comparar conjuntos de datos. Si dos conjuntos de datos tienen la misma media, pero una tiene una mayor dispersión, se puede inferir que hay una mayor variabilidad en los datos.
• Tomar decisiones informadas: la dispersión estadística es una herramienta fundamental para tomar decisiones informadas. Si se sabe que un conjunto de datos tiene una gran dispersión, puede ser más difícil hacer predicciones precisas o tomar decisiones basadas en esos datos.

¿Cómo se interpreta la dispersión estadística?

La dispersión estadística se interpreta como una medida de cuánto se separan los datos individuales de su valor central o promedio (por ejemplo, la media). En general, una dispersión alta indica que los datos están muy alejados de su valor central, mientras que una dispersión baja indica que los datos están más agrupados o cerca de su valor central.

Por ejemplo, si estás analizando la altura de un grupo de personas, una dispersión baja indicaría que la mayoría de las personas tienen alturas similares. Por su parte, una dispersión alta indicaría que las alturas de las personas varían significativamente.

Si estás analizando el rendimiento de un grupo de estudiantes en un examen, una dispersión baja indicaría que la mayoría de los estudiantes obtuvieron calificaciones similares, mientras que una dispersión alta indicaría que hay una gran variación en las calificaciones.

Es importante tener en cuenta que la interpretación de la dispersión estadística también depende del contexto en el que se utilice. Por ejemplo, en algunos casos, una alta dispersión puede ser deseable o esperada, mientras que, en otros casos, una baja dispersión puede ser más deseable.

¿Cuándo hay mayor dispersión en estadística?

En estadística, hay mayor dispersión cuando los datos de un conjunto están más separados entre sí, lo que indica una mayor variabilidad en los datos. Por ejemplo, si se están analizando los sueldos de un grupo de personas, una mayor dispersión indica que los sueldos varían más entre los individuos del grupo.

La medida más común de la dispersión estadística es la desviación estándar. Una desviación estándar alta indica que los datos están más dispersos, mientras que una desviación estándar baja indica que los datos están más cercanos a la media.

Otra medida de la dispersión estadística es el rango, que es la diferencia entre el valor máximo y el valor mínimo de un conjunto de datos. Si el rango es grande, indica que hay una gran variabilidad entre los datos.

¿Cómo saber si los datos están dispersos?

Para determinar si los datos están dispersos o no, es necesario calcular alguna medida de dispersión estadística, como la desviación estándar o el rango.

Si la medida de dispersión es alta, entonces los datos están más dispersos, lo que significa que hay más variabilidad en el conjunto de datos. Si la medida de dispersión es baja, entonces los datos están menos dispersos y hay menos variabilidad en el conjunto de datos.

También se puede visualizar la dispersión de los datos mediante gráficos estadísticos, como los diagramas de caja y bigotes o los histogramas. En estos gráficos, se puede ver la distribución de los datos y si están más o menos dispersos.

Además, se puede calcular la relación entre la media y la dispersión de los datos utilizando el coeficiente de variación, que es la desviación estándar dividida por la media multiplicada por 100. Un coeficiente de variación alto indica una gran dispersión relativa a la media, mientras que un coeficiente de variación bajo indica una baja dispersión relativa a la media.

¿Cuáles son las aplicaciones de la dispersión estadística?

La dispersión estadística tiene diversas aplicaciones en diferentes campos y disciplinas, entre ellas:

• Investigación científica: la dispersión estadística es una herramienta importante para el análisis de datos en diversas áreas de la ciencia, como la biología, la física, la psicología y la sociología. Se usa para analizar la variabilidad en los resultados de un estudio o experimento y para determinar si los resultados son significativos.
• Industria: se emplea para analizar la variabilidad en la producción de bienes y servicios, y para determinar si los procesos de producción son estables y consistentes.
• Economía: sirve para analizar la variabilidad en los precios de los bienes y servicios, y para determinar si los mercados son eficientes y equilibrados.
• Medicina: se utiliza para analizar la variabilidad en los resultados de los tratamientos médicos y para determinar si los tratamientos son efectivos y seguros.
• Educación: la dispersión estadística se usa para analizar la variabilidad en el rendimiento académico de los estudiantes y para determinar si las políticas y programas educativos son efectivos.

En resumen, la dispersión estadística es una herramienta útil en diversas áreas para analizar la variabilidad en los datos y tomar decisiones informadas basadas en la información obtenida.

Ejemplos de dispersión estadística

Llegado a este punto, veamos algunos ejemplos útiles sobre dispersión estadística, a continuación.

Ejemplo 1: Desviación estándar

Supongamos que tenemos los siguientes datos de una muestra de la edad de 10 personas en años: 20, 22, 18, 24, 19, 25, 21, 20, 23, 22. Para calcular la desviación estándar, seguimos los siguientes pasos:

Calcular la media de la muestra: (20+22+18+24+19+25+21+20+23+22) /10 = 21,4.

Restar la media de cada dato y elevar al cuadrado: (20-21,4)², (22-21,4)², (18-21,4)², (24-21,4)², (19-21,4)², (25-21,4)², (21-21,4)², (20-21,4)², (23-21,4)², (22-21,4)².

Sumar los resultados del paso 2: 138,16.

Dividir la suma del paso 3 entre el número de datos menos 1 (n-1): 138,16/9 = 15,35.

Calcular la raíz cuadrada del resultado del paso 4: √15,35 = 3,92.

Por lo tanto, la desviación estándar de la muestra es 3,92 años.

Ejemplo 2: Rango

Supongamos que tenemos los siguientes datos de una muestra de la altura de 10 personas en centímetros: 160, 170, 165, 180, 155, 185, 175, 170, 172, 168. Para calcular el rango, seguimos los siguientes pasos:

Ordenar los datos de menor a mayor: 155, 160, 165, 168, 170, 170, 172, 175, 180, 185.

Restar el valor mínimo al valor máximo: 185-155 = 30.

Por lo tanto, el rango de la muestra es de 30 cm.

Estos son solo dos ejemplos de cálculo de medidas de dispersión estadística. Hay muchas otras medidas, como el coeficiente de variación, el rango intercuartil, entre otros. Es importante elegir la medida de dispersión adecuada según la naturaleza de los datos y el objetivo del análisis.