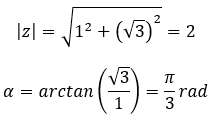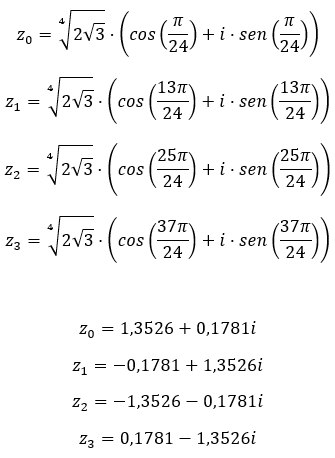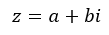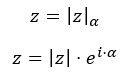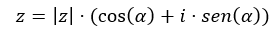Aritmetica

El binomio de Newton es una fórmula matemática que se utiliza para expresar la suma de dos términos elevados a una potencia determinada. Esta fórmula, que lleva el nombre del matemático británico Isaac Newton, se emplea en muchos campos de las matemáticas.

Por ejemplo, tiene utilidad en la estadística, la teoría de la probabilidad y el cálculo diferencial e integral. El teorema de binomio permite obtener el cálculo de la potencia de un binomio de forma sencilla.

En palabras simples, el binomio de Newton se basa en una fórmula con la cual se resuelve cualquier expresión algebraica de la forma (a+b)ⁿ. A pesar de que esta fórmula lleva su nombre por Isaac Newton, cabe mencionar que existe cierta controversia sobre su origen.

Es decir, algunas investigaciones apuntan a hallazgo del uso del teorema de binomio en el Oriente Medio.

¿Cuándo se desarrolló el binomio de Newton?

El teorema del Binomio de Newton, también conocido como Binomio de Newton, fue desarrollado en 1665 y comunicado por primera vez en dos cartas del funcionario de la Royal Society en 1676.

Estas cartas fueron una respuesta al matemático alemán Gottfried Wilhelm von Leibniz, quien buscaba conocimientos sobre investigaciones matemáticas en series infinitas. Newton compartió los resultados de su teorema, y Leibniz reconoció que era una técnica útil para obtener resultados en cuadraturas o series.

Este hallazgo permitió a Newton concluir que era posible operar con series infinitas de la misma manera que con expresiones polinómicas finitas. Aunque Newton nunca llegó a publicar su teorema, el matemático británico John Wallis lo publicó en su álgebra en 1685 y atribuyó su creación a Newton.

¿Por qué se llama binomio de Newton?

El binomio de Newton lleva el nombre del matemático y físico inglés, Isaac Newton, quien lo desarrolló en el siglo XVII. Newton no fue el primero en descubrir este teorema, pero sí fue el primero en demostrar su validez para cualquier número entero positivo n.

El binomio de Newton es una herramienta matemática muy útil en álgebra y cálculo, y se utiliza ampliamente en campos como la física, la estadística, la ingeniería y la informática.

¿Cuál es la fórmula del binomio de Newton?

Como bien mencionamos antes, el binomio de newton es la fórmula a través de la cual se pueden encontrar las potencias de un binomio. Para poder encontrar dicha potencia binomial se usan los “coeficientes binomiales”. El término anterior se refiere a las sucesiones de combinaciones.

Teniendo esto en cuenta, podemos desglosar las fórmulas del binomio de Newton de la siguiente forma:

• (a + b)² = a²+ 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b)³= a³ + 3a²b + 3 ab² + b³

Las expresiones matemáticas que se refieren al desarrollo de (a+b)ⁿ se conocen como entidades notables, y permiten obtener una fórmula general que representa esta operación para cualquier número entero natural “n”.

Al examinar los coeficientes de cada polinomio resultante, se puede notar una secuencia que sigue el llamado Triángulo de Pascal.

La secuencia del Triángulo de Pascal se inicia con el número 1, y en cada siguiente fila, los números de los extremos son siempre 1. Los valores intermedios se obtienen sumando los dos números de la fila anterior que se encuentran directamente encima del valor que se desea calcular.

¿Cómo hallar un término en el binomio de Newton?

Para hallar un término específico en el binomio de Newton se utiliza la fórmula general:

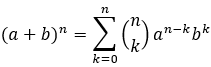
Donde:

a y b son los coeficientes del binomio.

n es el exponente del binomio.

k es el término específico que deseamos encontrar.

Σ representa la suma desde k=0 hasta n.

[n k] es el coeficiente binomial que se calcula mediante la siguiente fórmula: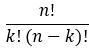

Por lo tanto, la fórmula completamente desarrollada queda tal que así:

Ejemplo de un binomio de Newton resuelto

Una vez que se tienen estos valores, se sustituyen en la fórmula y se resuelve la expresión para obtener el término específico. Por ejemplo, si deseamos encontrar el quinto término del binomio (2x + 3)⁶, se tendría:

a = 2x

b = 3

n = 6

k = 5

Entonces, utilizando la fórmula:

El quinto término corresponde a k=5, por lo que se tiene:

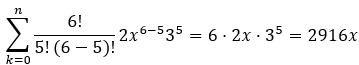
Por lo tanto, el quinto término del binomio (2x + 3)⁶ es 2916x.

¿Qué es un binomio de Newton de grado 5?

Un binomio de Newton de grado 5 es una expresión algebraica de la forma (a + b)⁵, donde “a” y “b” son variables y el exponente 5 indica el grado del binomio. Al expandir esta expresión, se obtiene un polinomio de quinto grado que tiene seis términos:

(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Cada término de este polinomio se obtiene combinando los coeficientes binomiales con las potencias de “a” y “b”. Por ejemplo, el segundo término (5a⁴b) se obtiene multiplicando el coeficiente binomial (5 elegir 1 = 5) por “a” elevado a la cuarta potencia y por b elevado a la primera potencia.

Los binomios de Newton de grado 5 son útiles en diferentes ramas de las matemáticas y la física, como la estadística, la teoría de la probabilidad y la mecánica cuántica.

¿Cuáles son las aplicaciones del binomio de Newton?

El binomio de Newton tiene una amplia variedad de aplicaciones en diversas áreas, entre ellas:

• Cálculo de probabilidades: el teorema del binomio es utilizado para calcular las probabilidades de eventos binomiales, como el lanzamiento de una moneda o el éxito o fracaso en una serie de pruebas.
• Teoría de números: el binomio de Newton se usa para expandir polinomios y simplificar ecuaciones en la teoría de números.
• Estadística: el binomio de Newton se emplea para calcular distribuciones binomiales y en la construcción de intervalos de confianza.
• Física: en física, el teorema del binomio se utiliza en la teoría de la relatividad y en la mecánica cuántica, entre otras áreas.
• Economía y finanzas: el binomio de Newton se usa para calcular el valor presente y futuro de flujos de efectivo en el tiempo y en la valoración de opciones financieras.
• Programación y ciencias de la computación: el binomio de Newton se emplea en el desarrollo de algoritmos y en la programación de computadoras.

¿Por qué es importante el binomio de Newton?

El binomio de Newton es relevante porque es una herramienta matemática fundamental para el desarrollo del álgebra y la teoría de números. Permite calcular el resultado de la elevación al cuadrado o a cualquier otra potencia de un binomio, lo que es de gran utilidad en la resolución de ecuaciones y la simplificación de expresiones algebraicas.

Además, tiene aplicaciones en áreas como la estadística, la probabilidad y la física, entre otras. En resumen, el binomio de Newton es un concepto esencial en las matemáticas y su comprensión es crucial para avanzar en muchos campos de estudio.

¿Existen otras formas de expresar el binomio de Newton?

Sí, existen otras formas de expresar el binomio de Newton. Por ejemplo, se puede expresar en términos de los coeficientes binomiales usando la notación combinatoria.

También, se puede expresar en términos de funciones exponenciales y funciones trigonométricas mediante la fórmula de Euler. Asimismo, en términos de la función gamma mediante la fórmula de Legendre. Estas expresiones alternativas pueden ser útiles en diferentes contextos y problemas matemáticos.

Ejemplos de binomio de Newton

A continuación, veamos algunos ejemplos sencillos de aplicación del binomio de Newton.

Ejemplo 1: Calcular el término de orden 3 en el desarrollo de (x + y)⁵.

Solución: En el desarrollo de (x + y)⁵, el coeficiente del primer término es 1, el coeficiente del segundo término es 5, el coeficiente del tercer término es 10, el coeficiente del cuarto término es 10, el coeficiente del quinto término es 5 y el coeficiente del sexto término es 1.

Por lo tanto, el término de orden 3 es:

10x²y³

Ejemplo 2: Hallar el término independiente en el desarrollo de (2x – 1)⁴.

Solución: En el desarrollo de (2x – 1)⁴, el término independiente se encuentra en la combinación (2x)^p(-1)^(4-p), donde p es el valor que hace que el exponente de (2x)^p y (-1)^(4-p) sumen 4.

Por lo tanto, el término independiente es:

(2x)²(-1)² = 4

Ejemplo 3: Encontrar el término de mayor grado en el desarrollo de (3x – 2y)⁶.

Solución: El término de mayor grado en el desarrollo de (3x – 2y)⁶ se encuentra en la combinación (3x)^p(-2y)^(6-p), donde p es el valor que hace que el exponente de (3x)^p y (-2y)^(6-p) sea igual al grado del binomio, que es 6.

Por lo tanto, el término de mayor grado es:

(3x)³(-2y)³ = -216x³y³

Los números impares son un conjunto de números enteros que no son divisibles entre 2. Es decir, aquellos que no tienen un resultado exacto al ser divididos entre 2. Por lo tanto, los números impares siempre terminan en 1, 3, 5, 7 o 9.

El conjunto de números impares incluye a -3, -1, 1, 3, 5, 7, 9, 11, 13, etc. Los números impares se utilizan en muchas áreas de las matemáticas, como en la teoría de números, la geometría, la estadística y la probabilidad, entre otras.

¿Cuándo surge el concepto de números impares?

El concepto de números impares es muy antiguo y se remonta a la antigua Grecia. El filósofo y matemático griego Pitágoras (570 a.C. – 495 a.C.) fue uno de los primeros en estudiar los números impares y pares.

De hecho, descubrió que los números impares podían ser representados por una línea, mientras que los números pares no podían. En el siglo III a.C., el matemático griego Euclides formalizó el concepto de números impares y pares en su obra “Elementos”, estableciendo las reglas básicas de su manipulación y operación.

¿Cuáles son las características de los números impares?

Los números impares tienen varias características que los distinguen de los números pares. Algunas de las características más importantes de los números impares son:

• No son divisibles por 2: a diferencia de los números pares, los números impares no pueden ser divididos exactamente por 2, por lo que siempre tienen un residuo de 1 cuando se dividen por 2.
• Pueden ser representados por la fórmula 2n+1: todos los números impares pueden ser escritos en términos de una variable n utilizando la fórmula 2n+1, donde n es un número entero.
• Forman una secuencia: los números impares forman una secuencia que comienza con 1 y continúa con 3, 5, 7, 9, y así sucesivamente.
• No son múltiplos de otros números impares: ningún número impar es un múltiplo de otro número impar, lo que significa que cada número impar tiene una identidad única.
• La suma de dos números impares siempre es un número par: cuando se suman dos números impares, el resultado siempre es un número par, ya que cada número impar tiene un “compañero” que lo hace par (por ejemplo, 1+3=4, 5+7=12, etc.).

Propiedades de los números impares

Algunas de las propiedades de los números impares son:

• Suma de números impares: La suma de dos números impares siempre dará como resultado un número par
• Resta de números impares: La resta de dos números impares siempre dará como resultado un número par.
• Multiplicación de números impares: La multiplicación de dos números impares siempre dará como resultado un número impar.
• División de números impares: La división de un número impar entre otro número impar puede dar como resultado un número par o un número impar.
• Potencia de números impares: Cualquier número impar elevado a cualquier potencia impar dará como resultado un número impar.
• Raíz cuadrada de números impares: La raíz cuadrada de un número impar siempre será un número irracional.
• Secuencia de números impares: Los números impares están dispuestos en una secuencia infinita y ordenada: 1, 3, 5, 7, 9, 11, 13, 15, 17, etc.

¿Cuál es la diferencia entre números pares y números impares?

Los números pares y los impares se diferencian principalmente en su divisibilidad por 2. Los números pares siempre pueden ser divididos por 2, mientras que los impares no. En cuanto a su representación decimal, los números pares terminan en 0, 2, 4, 6 u 8, mientras que los números impares terminan en 1, 3, 5, 7 u 9.

¿Cómo puedo identificar si un número es impar?

Para identificar si un número es impar, basta con verificar si su último dígito es 1, 3, 5, 7 o 9. Si el último dígito del número es cualquiera de estos, entonces el número es impar. Si el último dígito es 0, 2, 4, 6 u 8, entonces el número es par. También se puede dividir el número entre 2, si al hacerlo no resulta en un número entero, entonces es impar.

¿Cuántos resultados impares podemos obtener?

El número de resultados impares que podemos obtener depende de la operación matemática y de los números que se utilicen. Por ejemplo, si se suman dos números impares, siempre se obtendrá un resultado par.

Si se multiplican dos números impares, el resultado siempre será impar. Y si se eleva un número impar a cualquier potencia, el resultado siempre será impar.

En general, hay infinitos resultados impares posibles en matemáticas, ya que los números impares pueden ser utilizados en una amplia variedad de operaciones y contextos.

¿Qué es un número impar compuesto?

Un número impar compuesto es un número entero impar que tiene más de dos factores primos distintos. En otras palabras, es un número impar que se expresa como el producto de dos o más números primos distintos.

Por ejemplo, el número 15 es un número impar compuesto. Es decir, se expresa como el producto de los números primos 3 y 5. Otro ejemplo es el número 35, que se expresa como el producto de los números primos 5 y 7.

En contraste, un número impar primo es un número impar que solo se divide exactamente entre 1 y sí mismo. Es decir, solo tiene dos factores primos distintos. Ejemplos de números impares primos son 3, 5, 7, 11, 13, 17, etc.

¿Cuáles son las aplicaciones de los números impares?

Los números impares tienen diversas aplicaciones en varios ámbitos, entre ellas:

• Matemáticas: los números impares son fundamentales en la aritmética y la teoría de números, donde se utilizan en la resolución de problemas y en la demostración de teoremas.
• Tecnología: en la programación y la informática, los números impares son útiles para la indexación de listas y arreglos, y en la creación de algoritmos.
• Arte: en la música, se utilizan los números impares para crear patrones rítmicos y para la construcción de escalas y armonías. En la pintura y la escultura, se utilizan los números impares para lograr composiciones más estéticas y equilibradas.
• Juegos: en los juegos de mesa y de cartas, se utilizan los números impares para determinar el número de jugadores o de turnos.
• Superstición: en algunas culturas, se asocian ciertos números impares con la buena suerte o con la protección contra el mal de ojo, como el número 7 en la cultura occidental o el número 3 en la cultura oriental.

¿Cómo aprender los números impares de forma simple?

Aquí hay algunos consejos para aprender los números impares de forma sencilla:

• Repite los números en voz alta: recita los números impares en voz alta, desde el 1 hasta el número que desees, como el 100 o el 1000. Esto te ayudará a memorizar los números impares más fácilmente.
• Observa patrones: los números impares siguen un patrón. Por ejemplo, todos los números impares terminan en 1, 3, 5, 7 o 9. Presta atención a estos patrones y te será más fácil recordar los números impares.
• Aprende trucos mnemotécnicos: los trucos mnemotécnicos son una forma divertida de recordar los números impares. Por ejemplo, puedes recordar que el número 3 es impar porque se parece a una horquilla, que tiene 3 dientes. El número 5 es impar porque tiene 5 dedos en cada mano.
• Juegos de memoria: juega juegos de memoria para ayudarte a recordar los números impares. Por ejemplo, puedes jugar al juego de concentración con tarjetas que tengan números impares escritos en ellas.
• Practica regularmente: la práctica regular es la clave para aprender los números impares de forma sencilla. Dedica unos minutos cada día para repasar los números impares y pronto te los sabrás de memoria.

Recuerda que la paciencia y la constancia son importantes para aprender cualquier cosa, incluyendo los números impares.

Ejemplos fáciles de problemas matemáticos con números impares

• ¿Cuál es la suma de los primeros 10 números impares?

Solución: Los primeros 10 números impares son: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19. Sumando todos ellos: 1+3+5+7+9+11+13+15+17+19 = 100.

• Si un número impar se multiplica por otro número impar, ¿el resultado es par o impar?

Solución: El resultado de la multiplicación de dos números impares siempre es impar. Por ejemplo, 3 x 5 = 15 (impar).

• ¿Cuál es la diferencia entre la suma de los primeros 10 números impares y la suma de los primeros 10 números pares?

Solución: Los primeros 10 números pares son: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. La suma de los primeros 10 números impares es 100, mientras que la suma de los primeros 10 números pares es 110. La diferencia es 10.

• ¿Cuál es el resultado de la resta de un número impar y un número par?

Solución: La resta de un número impar y un número par siempre es un número impar. Por ejemplo, 7 – 2 = 5 (impar).

• Si un número impar se divide entre otro número impar, ¿el resultado es par o impar?

Solución: La división de dos números impares puede dar como resultado un número par o impar. Por ejemplo, 9 ÷ 3 = 3 (impar) y 15 ÷ 5 = 3 (impar).

Los números pares son aquellos que pueden ser divididos exactamente por 2. Es decir, cuyo residuo al ser divididos por 2 es cero. La sucesión de números pares es: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, y así sucesivamente, incrementándose de dos en dos.

Estos números se identifican visualmente, ya que todos los números terminados en 0, 2, 4, 6 u 8 son pares. Por ejemplo, los números 16, 212, 10, 456 y 88 son pares, porque todos ellos pueden ser divididos exactamente por 2. Es importante destacar que las propiedades matemáticas de los números pares son diferentes a las de los números impares.

En el ámbito de las matemáticas, los números pares son muy relevantes y se utilizan en diferentes áreas como la geometría, la aritmética y el álgebra. Por ejemplo, en la geometría, los puntos de coordenadas pares se ubican en el eje horizontal, mientras que los puntos de coordenadas impares se ubican en el eje vertical.

Además, en el álgebra, las funciones pares e impares son funciones matemáticas especiales que tienen propiedades únicas y se utilizan para simplificar cálculos y resolver problemas.

¿Cuándo surge el concepto de números pares?

El concepto de números pares es muy antiguo y se remonta a la antigua civilización egipcia y babilónica, que usaban sistemas numéricos basados en la numeración decimal.

Los antiguos griegos también estudiaron los números pares y se les atribuye la primera demostración formal de que la suma de los primeros n números pares es igual a n² + n.

En la Edad Media, los números pares se convirtieron en objeto de estudio en la teoría de números y se emplearon en varios campos de las matemáticas. Actualmente, los números pares tienen aplicaciones en muchas áreas diferentes, como la criptografía, la física, la electrónica y la ingeniería mecánica, entre otras.

¿Cuáles son las características de los números pares?

Los números pares tienen varias características que los definen. Algunas de las más destacadas son:

• Son divisibles por 2: esto significa que al dividir un número par por 2, el resultado será siempre un número entero, es decir, sin decimales ni residuos.
• Su última cifra es siempre 0, 2, 4, 6 u 8: al ser divisibles por 2, su última cifra siempre es una de estas opciones. Por ejemplo, los números 2, 4, 6, 8, 10, 12, etc., tienen una última cifra que es una de estas opciones.
• Se pueden representar en la forma 2n: cualquier número par puede ser representado como el producto de 2 y otro número entero. Por ejemplo, el número 10 puede ser representado como 2 x 5, y el número 24 como 2 x 12.
• Al sumar o restar números pares, el resultado siempre es un número par: esto se debe a que cuando se suman o restan dos números pares, el resultado es una combinación de números pares.
• Los números pares forman una secuencia alternada con los números impares: por ejemplo, la secuencia 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, etc., alterna entre números pares e impares.

En resumen, los números pares son aquellos que se pueden dividir por 2 y cuya última cifra es 0, 2, 4, 6 u 8. Además, se representan en la forma 2n y al sumar o restar números pares, el resultado siempre es un número par.

Propiedades de los números pares

Los números pares tienen algunas propiedades interesantes. Aquí hay algunas de ellas:

• Un número par se puede expresar como el doble de otro número. Por ejemplo, el número 6 es par y se puede expresar como 2 x 3.
• La suma o resta de dos números pares siempre da como resultado un número par. Por ejemplo, 4 + 6 = 10, que es un número par.
• La multiplicación de dos números pares siempre da como resultado un número par. Por ejemplo, 4 x 6 = 24, que es un número par.
• El producto de cualquier número par y cualquier número entero siempre es par. Por ejemplo, 2 x 5 = 10, que es un número par.
• En una serie aritmética, si el primer término es par y la diferencia común es par, entonces todos los términos de la serie son pares.
• Los números pares no tienen residuo cuando se dividen por 2. Esto se puede expresar matemáticamente como n % 2 = 0, donde n es un número par y % es el operador módulo, que devuelve el residuo de una división.
• En teoría de números, los números pares se caracterizan por tener un último dígito de 0, 2, 4, 6 u 8 en su representación decimal.

¿Cuál es la diferencia entre números pares y números impares?

La principal diferencia entre números pares e impares es que los números pares son divisibles por 2, mientras que los números impares no lo son. Además, los números pares tienen un último dígito de 0, 2, 4, 6 u 8 en su representación decimal, mientras que los números impares tienen un último dígito de 1, 3, 5, 7 u 9.

¿Cómo puedo identificar si un número es par?

Para identificar si un número es par o impar, debes verificar si es divisible por 2. Si el número se puede dividir por 2, entonces es par. Si no es divisible por 2, entonces es impar. Por ejemplo, el número 4 es divisible por 2 y, por lo tanto, es par, mientras que el número 7 no es divisible por 2 y como resultado es impar.

¿Por qué el 0 es un número par?

El 0 se considera un número par porque es divisible por 2. En otras palabras, el 0 se puede escribir como 2 veces cualquier número entero, lo que cumple con la definición de un número par.

Además, el 0 tiene un último dígito de 0 en su representación decimal, al igual que otros números pares como el 2, 4, 6, 8, etc. Por lo tanto, aunque el 0 no tiene una naturaleza “par” o “impar” obvia como otros números, se le clasifica como un número par por definición y por convención matemática.

¿Cuál es el único número primo y par?

Hay un único número primo par, y es el número 2. El número 2 es el único número primo que es par. Todos los demás números pares son divisibles por 2 y, por lo tanto, no son primos.

Para ser un número primo, un número debe ser mayor que 1 y solo ser divisible por 1 y por sí mismo. El número 2 cumple con estas condiciones. Por ello, es un número primo.

¿Cuál es el uso de los números pares?

Realmente, los números pares tienen muchos usos y aplicaciones. Veamos algunos de los más importantes, a continuación.

• Matemáticas: los números pares son aquellos que se pueden dividir exactamente entre dos. En matemáticas, los números pares son fundamentales en temas como la aritmética, el álgebra, la geometría y la estadística.
• Programación: En programación, los números pares se utilizan en ocasiones para realizar acciones específicas. Por ejemplo, en algunos lenguajes de programación, el número par se emplea para indicar que un archivo está listo para ser leído o escrito.
• Arquitectura: en arquitectura, los números pares se usan para definir los diseños de edificios y estructuras. Por ejemplo, si un arquitecto está diseñando una casa con una fachada simétrica, es probable que use un número par de ventanas para lograr esa simetría.
• Música: los números pares pueden emplearse en la música para crear patrones rítmicos. Por ejemplo, muchos ritmos de música electrónica se basan en patrones de dos tiempos, que corresponden a números pares.
• Juegos: en los juegos de mesa, los números pares se utilizan para definir el número de jugadores o las reglas del juego. Por ejemplo, muchos juegos de mesa están diseñados para ser jugados por dos, cuatro o seis jugadores.

¿Cómo aprender números pares de forma simple?

Aquí hay algunas formas simples de aprender los números pares:

• Repasar la tabla de multiplicar del 2: aprender la tabla de multiplicar del 2 es una forma fácil de recordar los números pares. Comienza por el número 2 y sigue multiplicando por 2 para obtener los siguientes números pares: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, etc.
• Observar el patrón: los números pares siempre tienen un último dígito de 0, 2, 4, 6 u 8 en su representación decimal. Observa este patrón y verás que es fácil identificar rápidamente los números pares.
• Juegos de memoria: jugar juegos de memoria puede ser una forma divertida de aprender los números pares. Por ejemplo, puedes hacer un juego de cartas con tarjetas que tengan números pares escritos en ellas y practicar emparejar los números pares correspondientes.
• Practicar con problemas matemáticos: resuelve problemas matemáticos que involucren números pares. Esto te ayudará a familiarizarte con ellos y a comprender mejor las propiedades matemáticas de los números pares.

Ejemplos fáciles de problemas matemáticos con números pares

• ¿Cuántos números pares hay entre 1 y 50?

Solución: Los números pares entre 1 y 50 son: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48 y 50. Por lo tanto, hay 25 números pares en este rango.

• ¿Cuál es la suma de los primeros 10 números pares?

Solución: Los primeros 10 números pares son: 2, 4, 6, 8, 10, 12, 14, 16, 18 y 20. Para encontrar la suma, simplemente los sumamos: 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 = 110.

• ¿Cuál es el doble del número 16?

Solución: El número 16 es un número par, por lo que su doble es fácil de encontrar. Simplemente, lo multiplicamos por 2: 16 · 2 = 32.

• ¿Cuál es el número par más grande que es menor que 100?

Solución: El número par más grande que es menor que 100 es 98.

El número de Euler (también conocido como la constante de Euler) es un número matemático importante y esencial en diversas áreas de las matemáticas, incluyendo la teoría de números, la topología, la teoría de grupos y la teoría de funciones. Se representa con la letra griega «e» y su valor aproximado es 2,71828.

El número e surge de la fórmula de la función exponencial y es un número fundamental en la teoría de los números complejos.

También es un número natural que aparece en la resolución de muchos problemas matemáticos, incluyendo el cálculo de probabilidades y la modelización de procesos de crecimiento y decay.

¿Cuál es el origen del número Euler?

El número de Euler fue nombrado en honor al matemático suizo Leonhard Euler (1707-1783), quien fue uno de los más grandes matemáticos de todos los tiempos y es considerado el padre de la matemática moderna.

Euler hizo valiosas contribuciones en muchas áreas de las matemáticas, incluyendo la teoría de números, la geometría, el cálculo, la física y la astronomía.

Fue él quien primero definió y utilizó el número e (llamado el número de Euler) en su trabajo en cálculo y teoría de logaritmos. La fórmula de Euler para números complejos también es una de sus contribuciones más notables a la matemática.

¿Cómo se obtiene este valor?

A decir verdad, hay diversos métodos para calcular el número de Euler. Sin embargo, cabe mencionar que ningún método arroja un resultado exacto. Por lo tanto, su numeración es continúa e infinita, pero no se repite.

De hecho, en la actualidad, se conocen hasta más de 1 billón de números que forman la cifra del número e. La serie infinita que define el número de Euler es:

Donde «!» es factorial, que se define como el producto de todos los números naturales hasta ese número. Por ejemplo:

5! = 5 · 4 · 3 · 2 · 1 = 120

Podemos ver gráficamente esta serie como la suma de una serie de rectángulos con altura 1 y anchura decreciente, donde la anchura de cada rectángulo es 1/n!, donde n es el número de factoriales.

Si aumentamos el número de rectángulos en la suma, la aproximación al área bajo la curva de la función exponencial se acerca cada vez más al número de Euler.

En resumen, el número de Euler es un número que surge de la suma de una serie infinita y es fundamental en muchas áreas de las matemáticas. Aunque es un número irracional, su valor aproximado es 2,71828.

Es importante tener presente que el mismo Euler implementó este método para realizar el cálculo de e con 18 decimales.

Otra forma de calcularlo:

Podemos calcular el valor aproximado del número de Euler en una recta utilizando una serie de términos finitos. Por ejemplo, si tomamos la primera serie infinita que se definió anteriormente:

Podemos calcular el valor aproximado sumando los primeros términos de la serie. Por ejemplo, si sumamos los primeros 6 términos:

Podemos representar esta serie en una recta para ver cómo se acerca al valor aproximado de 2,71828.

Gráficamente, la recta que representa el número de Euler se puede dibujar con una serie de rectángulos con altura 1 y anchura decreciente, donde la anchura de cada rectángulo es 1/n!, donde n es el número de factoriales.

Si aumentamos el número de rectángulos en la suma, la aproximación al área bajo la curva de la función exponencial se acerca cada vez más al número de Euler.

Ecuaciones exponenciales con el número Euler

Las ecuaciones exponenciales con el número de Euler pueden ser usadas para modelar una amplia variedad de fenómenos en ciencias como la física, la biología, la economía, entre otros. Algunos ejemplos incluyen:

Crecimiento y decadencia exponencial

Este modelo describe la tasa en la que una población crece o decrece, o la tasa de descomposición de una sustancia tóxica.

Por ejemplo, si una población está creciendo a una tasa del 5% por año, su tamaño puede ser descrito por la fórmula:

P(t) = P0 · e^0,05t, donde P0 es el tamaño inicial de la población.

Modelos de desintegración radioactiva

 Este modelo describe la tasa en la que los átomos radiactivos se desintegran con el tiempo.

La fórmula es la siguiente:

N(t) = N0 · e^-λt

Donde N0 es el número inicial de átomos, λ es una constante que depende del material radioactivo y t es el tiempo.

Estos son solo algunos ejemplos de cómo se pueden emplear las ecuaciones exponenciales con el número de Euler en la práctica. Hay muchos otros campos en los que las ecuaciones exponenciales son útiles y relevantes.

¿Cuáles son las aplicaciones del número Euler?

El número de Euler tiene una amplia gama de aplicaciones en diferentes campos de la matemática y las ciencias. Algunos de los campos en los que se utiliza el número e son los siguientes:

• Cálculo y análisis matemático: se utiliza en el estudio de las funciones exponenciales y logarítmicas, y en la solución de ecuaciones diferenciales.
• Teoría de números: se utiliza en el estudio de la distribución de los números primos y en la solución de problemas relacionados con la teoría de números.
• Probabilidad y estadística: se emplea en la solución de problemas relacionados con la distribución de probabilidad y en la estimación de valores esperados.
• Criptografía: se usa en el estudio de los algoritmos de cifrado y descifrado.
• Física: se utiliza en la solución de problemas relacionados con la termodinámica, la mecánica cuántica y la física estadística.
• Química: se emplea en la solución de problemas relacionados con la termodinámica química y la cinética química.

Fórmula de Euler para números complejos

La fórmula de Euler para números complejos establece una relación entre las funciones trigonométricas y exponenciales. La fórmula se escribe como:

Donde “e” es la base de los logaritmos naturales, “i” es la unidad imaginaria, ”x” es un número real y “cos” y “sen” son las funciones trigonométricas coseno y seno, respectivamente.

Esta fórmula es muy útil en muchas áreas de la matemática, incluyendo la teoría de números, la teoría de funciones y la teoría de la complejidad, y tiene una gran variedad de aplicaciones en la ingeniería, la física y la economía.

Un ejemplo práctico de su uso es en la representación de señales y sistemas en el análisis de Fourier, en el cual las señales periódicas se representan como una suma de señales sinusoidales complejas.

La fórmula de Euler se utiliza para describir la forma en que estas señales complejas se relacionan con las funciones trigonométricas reales que describen las señales sinusoidales individuales.

El número Euler y el interés compuesto

El interés compuesto es un concepto financiero que describe el proceso por el cual una cantidad de dinero, llamada capital, genera intereses sobre el interés acumulado a lo largo del tiempo.

En otras palabras, los intereses generados por una inversión no solo provienen del capital inicial, sino también de los intereses generados en períodos previos.

El número de Euler y el interés compuesto están relacionados porque la fórmula para calcular el interés compuesto utiliza el número de Euler. La fórmula para el interés compuesto es:

A = P · e^rt

Donde A es el monto final, P es el principal, r es la tasa de interés, t es el tiempo y e es el número de Euler. De esta manera, el número de Euler es un factor importante en la formulación matemática para el cálculo del interés compuesto.

Un ejemplo de cálculo de interés compuesto con números concretos sería el siguiente:

Supongamos que tenemos una inversión de 1000 € a una tasa de interés del 5% anual durante 2 años. La fórmula para calcular el interés compuesto sería:

A = P · e^rt = 1000 · e^{0,05 · 2} = 1000 · 1,1025 = 1102,5 €.

Esto significa que después de 2 años, nuestro capital inicial de 1000 € habrá crecido a 1102,5 € debido al interés compuesto generado.

Ejemplos de ejercicios matemáticos con el número Euler

Aquí están dos ejemplos de ejercicios resueltos de matemáticas que involucran el número de Euler:

1. Encuentra el valor de «e^ix» donde x es un número real:

La identidad de Euler nos dice que e^ix = cos(x) + i · sen(x). Por lo tanto, si conocemos el valor de x, podemos calcular el valor de e^ix utilizando las funciones trigonométricas.

2. Calcula e^(x²) para un valor dado de x:

Podemos utilizar la serie de Taylor para calcular el valor de e^(x²). La serie de Taylor de e^x es una expansión infinita que permite calcular aproximaciones sucesivas del valor de e^x, dependiendo del término que se use.

Si sustituimos x² en lugar de x en esta serie, obtenemos la serie de Taylor para e^(x²).

Si quieres practicar restas sin llevar, te recomendamos que le eches un vistazo a las fichas que te proporcionamos en este artículo, seguro que te serán de ayuda. Aunque, si lo que quieres es aprender a restar, te recomendamos que accedas a este último enlace. Allí te explicaremos cómo hacerlo de una forma fácil y rápida.

Ejercicios de restas de una cifra sin llevar

Las restas de una cifra sin llevar es el nivel más fácil de este tipo de operaciones. Puesto que solamente operamos con unidades, de momento no hay decenas ni centenas. Así que, únicamente debemos pensar en un dígito.

A continuación, te dejamos una serie de ejemplos, para que trates de resolverlos. Y recuerda que si quieres descargarte esta ficha de restas de una sola cifra, puedes hacerlo por medio de este botón:

Ejercicios de restas de dos cifras sin llevar

Las restas de dos cifras sin llevar son algo más complicadas que las anteriores, porque además de tratar con las unidades, debemos fijarnos en las decenas. Lo bueno es que el procedimiento es el mismo: solo hay que restar el número de arriba (el minuendo) al valor de abajo (sustraendo) en las unidades y después, en las decenas.

En las siguientes imágenes puedes encontrar varios ejemplos de este tipo de restas, para que trates de resolverlos. Te recomendamos que empieces por resolver la primera página y si te gusta cómo vas, puedes seguir con las dos páginas siguientes. O incluso, puedes bajar hasta el siguiente nivel: las restas de tres cifras sin llevar.

Ejercicios de restas de tres cifras sin llevar

En tercer lugar, encontramos las restas de tres cifras sin llevar, las cuales son un poco más complicadas de resolver. Eso sí, el procedimiento a seguir, para resolverlas, es idéntico que el anterior, pero hay que tener en mente las centenas. Que son la tercera cifra del sistema de numeración decimal.

A continuación, te mostramos unas cuantas restas de este tipo para que practiques. Si te va mejor, puedes pulsar en el botón «Descarga la ficha» y podrás descargarla para posteriormente imprimirla. Recuerda que lo importante es practicar, puesto que cuantos más ejercicios resuelvas, mejor sabrás restar sin llevar.

Ejercicios de restas de cuatro cifras sin llevar

Por último, llegamos a las restas de cuatro cifras sin llevar, las cuales son el tipo de restas más complicado que veremos hoy. Aunque, tal como llevamos diciendo todo el rato, hay que aplicar el mismo procedimiento para todas estas restas. Desde las de una cifra sin llevar hasta las de cuatro cifras sin llevar.

Para que puedas practicar un poco, te dejamos una serie de ejemplos en las siguientes imágenes. Y recuerda que si quieres descargar la ficha, solamente tienes que pulsar el siguiente botón.

Resolver potencias de números complejos es algo bastante sencillo de hacer, si conoces el método adecuado. Es por eso, que en este artículo, te explicaremos cómo resolver potencias complejas de tres formas: para números complejos en forma binómica, en forma polar y en forma trigonométrica.

¿Cómo se resuelve la potencia de un número complejo?

Tal como hemos dicho en la introducción, se nos pueden plantear tres situaciones, a la hora de operar con potencias complejas. La primera y más fácil es cuando nos dan el número en forma polar. La segunda es cuando nos dan el número en forma binómica y la tercera es cuando nos dan el número en forma trigonométrica.

Dicho de otro modo, cuando operamos con complejos en forma polar, el ejercicio se puede resolver más rápido. Por eso, se recomienda pasar el número en cuestión a forma polar. Pero, en realidad, todos los métodos son sencillos de resolver. Dicho esto, vamos a explicar cómo se resuelven todos los casos y te plantearemos algún ejercicio.

Potencias de números complejos en forma polar

Cuando queremos resolver potencias complejas en forma polar, sencillamente, debemos elevar el módulo a n y multiplicar el argumento por n. Expresado matemáticamente, obtenemos la siguiente fórmula:

A continuación, te planteamos algunos ejemplos, para que trates de resolverlos por tu cuenta:

Potencias de números complejos en forma binómica

Por otro lado, cuando queremos resolver potencias complejas en forma binómica, podemos recurrir a dos métodos diferentes. El primero se trata de resolver la potencia de manera «algebraica» (resolviendo como si la i fuera una variable). Y el segundo sistema se trata en convertir la forma binómica a polar y después, seguir el procedimiento de antes.

Si no sabes cómo pasar de la forma binómica a la polar, te lo explicamos de forma muy clara en nuestro artículo sobre los números complejos. Aunque, ahora lo veremos rápidamente con un ejemplo.

Trata de resolver la siguiente potencia compleja: (2 + 3i)².

Potencias de números complejos en forma trigonométrica

Por último, cuando queremos resolver potencias complejas en forma trigonométrica, debemos utilizar la conocida fórmula de Moivre. La cual se escribe tal que así:

Conociendo esta fórmula, trata de resolver los siguientes ejercicios:

Más sobre las potencias complejas

• Números complejos
• Propiedades de los complejos
• Operaciones de números complejos
• Raíces complejas

Calcular raíces de números complejos es algo bastante sencillo. Pues, una vez entiendes el procedimiento, este es bastante repetitivo. A continuación, vamos a explicarlo y te plantearemos algún ejemplo, para que aprendas a aplicarlo en ejercicios reales.

Raíces enésimas de números complejos

El concepto de raíz enésima equivale a decir raíz de orden n, por lo tanto, el mismo método sirve para calcular la raíz cuadrada y la raíz quinta de un número complejo. Eso sí, el número de soluciones cambiará en función de ese orden.

Por ejemplo, si calculamos la raíz cuarta de un complejo, obtenemos 4 soluciones diferentes. Y si lo expresamos en el plano complejo, podemos ver que se forma un polígono regular de 4 lados, centrado en el origen del plano. Esta es una propiedad muy interesante, que veremos en detalle más adelante (en el apartado de los ejemplos).

Ahora que ya hemos clarificado este concepto, vamos a ver cómo se calcula la raíz de un número complejo en forma polar (usar esta notación es la más cómoda para resolver una raíz.). Sencillamente, hay que calcular la raíz del módulo y expresar el argumento en función de n. Dicho de otra manera, la raíz del siguiente número complejo (z):

Equivale a calcular:

• Módulo: La raíz enésima del módulo inicial.
• Argumento: Sumarle al argumento 2πk en radianes o 360k en grados, y dividirlo todo entre n.

Matemáticamente, para calcular el módulo y el argumento usamos las siguientes dos fórmulas:

Donde, k = 0, 1, 2, …, n-1.

Y, por lo tanto, el resultado lo expresamos tal que así:

Para que quede claro, las n soluciones que obtendremos de resolver esta raíz estarán formadas por el mismo módulo y n argumentos diferentes.

Ejemplos del cálculo de raíces enésimas de complejos

Ahora vamos a ver un par de ejemplos sobre el cálculo de raíces enésimas de números complejos. Te recomendamos que trates de resolverlos por tu cuenta y cuando acabes, mires la corrección. Recuerda que el método está explicado justo arriba.

Calcula la raíz tercera del número complejo: 1 + i√3.

Calcula la raíz cuarta del número complejo: 3+i√3.

Más sobre raíces de números complejos

• Números complejos
• Operaciones de números complejos
• Potencias complejas
• Propiedades de los números complejos

Los números romanos son un sistema numérico que se utilizó en la antigua Roma y en la Edad Media. Este sistema se caracteriza por usar letras mayúsculas para representar valores numéricos.

Es decir, cada una de las cifras se representa por medio de una letra o la combinación de varias. La cantidad obtenida tiene que ver con el posicionamiento de las letras. Además, a diferencia de otros sistemas numéricos, los números romanos no tienen un símbolo para el cero.

Este sistema de numeración se compone de siete letras mayúsculas: I (1), V (5), X (10), L (50), C (100), D (500) y M (1000). Los valores de estas letras pueden combinarse para representar números más grandes. Por ejemplo, el número 11 se puede representar como XI (10 + 1), mientras que el número 123 se puede representar como CXXIII (100 + 20 + 3).

Un dato interesante sobre los números romanos es la forma en que se solía expresar el número 4. Es decir, en la antigüedad, el número 4 se representaba como “IIII”. Sin embargo, ahora mismo, se representa como “IV” debido a que no se debe repetir un mismo signo más de tres veces consecutivamente.

¿Cuál es el origen de los números romanos?

El origen exacto de los números romanos es incierto y ha sido objeto de debates entre historiadores y arqueólogos. Sin embargo, se cree que se desarrollaron a partir de los sistemas numéricos utilizados por los antiguos etruscos y griegos que habitaban en la región italiana en la época prerromana.

Se piensa que los primeros números romanos eran simples marcas en tablas de madera o en tela. Dichos símbolos eran utilizados para llevar un registro de transacciones comerciales y otros asuntos prácticos.

Con el tiempo, estas marcas evolucionaron en un sistema más sofisticado que empleaba letras mayúsculas para representar valores numéricos, y que se usó ampliamente en la antigua Roma y en la Edad Media.

¿Cómo funcionan los números romanos?

Los números romanos funcionan mediante la combinación de siete letras mayúsculas diferentes: I, V, X, L, C, D y M. Cada letra representa un valor numérico diferente:

I = 1

V = 5

X = 10

L = 50

C = 100

D = 500

M = 1000

Para formar números más grandes, se combinan estas letras de una manera específica. Aquí hay algunos ejemplos para ilustrar cómo funcionan los números romanos:

Para representar números compuestos por unidades, se escriben tantos símbolos “I” como unidades se requieran. Por ejemplo, para representar el número 3, se escriben tres símbolos “I”: III.

Para representar números que incluyen cinco unidades, se usa el símbolo “V”. Por ejemplo, para representar el número 5, se escribe “V”.

Para representar números compuestos por unidades y cinco unidades, se combinan los símbolos “I” y “V”. Por ejemplo, para representar el número 4, se escribe “IV” (un símbolo “I” antes de un símbolo “V”).

Para representar números mayores que 1000, se escriben tantos símbolos “M” como miles se requieran. Por ejemplo, para representar el número 2500, se escriben dos símbolos “M”: MM.

¿Cuáles son las 5 reglas de los números romanos?

Las cinco reglas principales de la numeración romana son las siguientes:

1. Los números se leen de izquierda a derecha.

• Ejemplo: Si escribimos el número XXV, debemos empezar a operar desde la izquierda: 10 + 10 + 5 = 25.

2.      Una letra no puede repetirse más de tres veces seguidas.

• Ejemplo: Para representar el número 30, en lugar de escribir “IIIIIIIIII…”, se escribe “XXX” (tres símbolos “X”).

3.      Para representar un número más grande, se coloca una letra con un valor numérico mayor a la derecha de letras con valores numéricos menores. De esta forma, se suman los valores. En el siguiente apartado, detallamos qué números pueden restarse, así que te recomendamos que mires ese apartado.

• Ejemplo: Para representar el número 39, se escribe “XXXIX” (tres símbolos “X” seguidos de un símbolo “I” y un símbolo “X”).

4.      Cuando se coloca una letra con un valor numérico menor a la izquierda de una letra con un valor numérico mayor, este valor se resta.

• Ejemplo: Para representar el número 4, en lugar de escribir “IIII”, se escribe “IV” (un símbolo “I” antes de un símbolo “V”).

5.      Los símbolos “V” y “L” no pueden colocarse a la izquierda de una letra con un valor numérico mayor, y los símbolos “I”, “X” y “C” solo pueden restarse.

• Ejemplo: Para representar el número 49, en lugar de escribir “VL”, se escribe “XLIX” (un símbolo “X” antes de un símbolo “L” y un símbolo “I”).

Estas reglas ayudan a asegurar que cada número romano sea único, fácil de leer y comprender. Al seguir estas reglas, se pueden representar todos los números enteros de una manera clara y concisa.

¿Cómo se clasifican los números romanos?

Una forma de comprender mejor cómo funcionan los números romanos es entender su clasificación. Puesto que los números de un mismo tipo, siguen las mismas normas a la hora de sumar y restar valores cuando están combinados con otras letras. Este sistema numérico se clasifica en los siguientes tres tipos:

1.     Aquellos que se pueden sumar o restar de acuerdo con la posición en la que se encuentren y que se pueden repetir hasta 3 veces. Asimismo, solo se escriben una única vez si es que están restándose:

I	Representa al número 1 y se resta solo de los símbolos V y X
X	Representa al número 10 y se resta solo de los símbolos L y C
C	Representa al número 100 y se resta solo de los símbolos D y M

2.     Los símbolos que no se repiten en ningún caso, pero cada uno representa el valor x5 de cada uno de los mencionados antes. Asimismo, siempre se suman:

V	5
L	50
D	500

3.     Este último símbolo de la clasificación, se puede escribir hasta tres veces continúas, pero solo suma. Por ello, nunca se usa para restar:

M

100

¿Cómo representar números del 4.000 en adelante en números romanos?

Para poder expresar una cantidad mayor a 3.999 en números romanos, no es necesario colocar letras hasta llegar a la cifra. En este caso, basta con colocar una raya encima del número, de esta manera lo estamos multiplicando por 1.000. Veamos algunos ejemplos a continuación:

Por otro lado, cabe destacar que, en el sistema de números decimales, cualquier combinación de cifras se lee como un número correcto. Sin embargo, esto no es igual en el caso de los números romanos.

Es decir, cuando aprendemos cómo leer la numeración romana no tiene sentido escribir “VV”, por ejemplo. Porque, sabemos que “VV“, en realidad se escribe con el símbolo “X“. Puesto que 5 + 5 = 10.

¿Cuál es la diferencia entre la numeración etrusca y la numeración decimal?

La numeración etrusca es un antiguo sistema numérico utilizado por la civilización etrusca de Italia.

La numeración decimal, por otro lado, es un sistema numérico basado en la posición, donde cada posición representa un factor de 10. Es el sistema numérico más comúnmente empleado en el mundo moderno, y se remonta a la antigua civilización hindú.

La principal diferencia entre ambos sistemas es la base. Mientras que la numeración decimal es un sistema basado en el número 10, la numeración etrusca era un sistema sexagesimal, basado en el número 60.

Esto significa que los etruscos empleaban una combinación de signos para representar números hasta 60, en lugar de solo los dígitos 0-9 que empleamos en el sistema decimal.

Además, la numeración etrusca no tenía un símbolo para el cero, lo que hacía más complicado llevar a cabo operaciones matemáticas complejas. Por otro lado, la numeración decimal, con su símbolo para el cero, es mucho más flexible y permite una amplia gama de operaciones matemáticas.

Para entender un poco mejor, veamos ejemplos de ambas formas de representación numérica a continuación:

Numeración decimal	Numeración romana
42	XLII
99	XCIX
2021	MMXXI

¿Cómo se pronuncian correctamente los números romanos?

No todas las personas saben cómo se deben pronunciar estos números. Mayormente, esto tiene que ver con la poca utilización que tienen los números romanos en la actualidad. No obstante, ahora mismo se leen y pronuncian como los números ordinarios del sistema decimal occidental.

Para ello, atienden a su valor real. Ahora bien, en el caso de su uso escrito, se aplica de la siguiente manera:

• Para identificar libros o capítulos se escribe Capítulo II y se lee como capítulo dos.
• Para señalar escenas en una obra teatral se escribe Acto IV y se lee como acto cuatro.
• Finalmente, para mencionar reyes, emperadores o papas se escribe Juan Pablo II y se lee Juan Pablo segundo.

¿Para qué se utilizan los números romanos en la actualidad?

Aunque los números romanos ya no se emplean como sistema de numeración en el día a día, aún tienen algunos usos importantes en la actualidad. Algunos de ellos son:

• Numeración de capítulos y páginas en libros: muchos libros, especialmente libros académicos y de texto, utilizan números romanos para numerar los capítulos y páginas iniciales.
• Nombres de monarquías y reinados: muchos países europeos, incluida la Reina Isabel II del Reino Unido, usan números romanos para identificar a los monarcas y reinados.
• Arquitectura y monumentos: algunos edificios y monumentos históricos, como iglesias, palacios y estatuas, utilizan números romanos para identificar los pisos o secciones.
• Designación de sistemas de medidas: diversos sistemas de medidas, como las dimensiones de las hojas de papel, emplean números romanos para identificar tamaños específicos.

En resumen, los números romanos aún se usan en la actualidad en una variedad de contextos, pero su utilización es principalmente ceremonial y decorativo.

Los números complejos son un conjunto formado por números reales y números imaginarios. Estos dos últimos conjuntos numéricos pueden representarse gráficamente por medio de la recta real y la recta imaginaria. Y cuando situamos ambas rectas en un mismo plano, se forma el conocido plano complejo.

¿Qué es el plano complejo?

El plano complejo está formado por el eje real (eje X), el cual es equivalente a la recta real y, por otro lado, el eje imaginario (eje Y), el cual conceptúa la recta imaginaria.

Cabe destacar, que este plano comprende todos los números complejos. Por lo tanto, da igual qué tan grande o tan pequeño, o en que forma esté escrito un número complejo, que este se puede graficar en el plano. Así que vamos a ver cómo se representan estos números en el plano complejo.

¿Cómo graficar números complejos en el plano complejo?

Como ya sabemos (o si no lo sabes, te recomendamos que leas nuestro artículo sobre los números complejos), existen tres formas de escribir un complejo: forma binómica, forma polar y forma trigonométrica. Cada una expresa el valor complejo siguiendo una estructura diferente, así que el método a seguir para hacer las representaciones gráficas es distinta.

A continuación, te explicamos el procedimiento a seguir en los tres casos:

Representación en forma binómica

Cuando tenemos un número complejo en notación binómica, que es la más habitual, debemos fijarnos en la estructura del número:

Donde, a es la parte real y b es la parte imaginaria.

Sabiendo esto, deducimos que el valor de a es el que utilizamos para la coordenada x (eje real) y el valor de b es el que usamos para la coordenada y (eje imaginario). Con el siguiente ejemplo, lo vas a entender mejor.

Vamos a tratar de representar el número: 3 + 2i.

Lo primero es dibujar el gráfico (señalizando que el eje horizontal es el real y el eje vertical es el imaginario):

Después, ubicamos el punto del gráfico en coordenadas cartesianas (x, y), que hemos deducido a partido del número complejo. En este ejemplo práctico, nuestro punto es el (3, 2).

Así quedaría representado el valor 3 + 2i en el plano complejo.

Representación en forma polar

Ahora vamos a ver, cómo se representa un número complejo en forma polar. Para entender bien este método, debes saber que la notación polar define un número complejo a partir del módulo y del argumento. Los cuales se emplean en la representación gráfica como coordenadas polares (¡no coordenadas cartesianas!).

Y la característica principal del sistema de coordenadas polares es que se describe la ubicación de un punto, por medio de un vector y un ángulo (no como el anterior método). Los cuales se corresponden con el módulo y argumento de los números complejos. A continuación, te mostramos la fórmula universal de la forma polar de un número complejo:

Donde |z| es el módulo y α es el argumento. Estas dos variables se traducen en el plano como:

• Módulo: es la longitud que define a un vector (entre el origen y el punto equivalente a nuestro número).
• Argumento: es el ángulo que forma el vector con el eje X.

Por lo tanto, el módulo de un número complejo se corresponde con la longitud del vector que utilizamos para hacer la representación gráfica. Mientras que el argumento o ángulo del número complejo, se corresponde con el ángulo que hay entre el vector y el eje X. A continuación, puedes ver un esquema que sitúa todas las variables:

Ahora, vamos a tratar de representar el número: 3₄₅.

Primero, debemos identificar el módulo y el argumento:

• Módulo: 3.
• Argumento: 45 grados.

Seguidamente, debemos encontrar los puntos de la gráfica que tienen un módulo igual a 3, en este caso nos sirve cualquier punto de una circunferencia de radio 3.

Y para acabar de determinar cuál es el punto exacto, debemos poner la condición de que el vector generado por el módulo y el origen deben hacer un ángulo de 45 grados con el eje X.

Y ya tenemos representado un número complejo en notación polar.

Representación en forma trigonométrica

Por último, nos queda explicar cómo se representa un número complejo en forma trigonométrica. Este caso y el anterior son prácticamente iguales, esto se debe a que tanto la forma polar como la forma trigonométrica, usan los mismos datos para expresar un número complejo: el módulo y el argumento. Solo cambia la estructura de la expresión:

Donde, |z| es el módulo y α es el argumento.

Así que debemos aprovechar el mismo método que en el anterior caso: emplear el módulo como «longitud» y el argumento como el ángulo. Viendo el siguiente ejemplo, lo entenderás mejor.

Vamos a representar z = 4 · (cos (45) + i · sen(45)).

Lo primero es identificar el módulo y el ángulo:

• Módulo: 4.
• Argumento: 45 grados.

Después, debemos encontrar los puntos de la gráfica que tienen un módulo igual a 4, en este caso nos sirve cualquier punto de una circunferencia de radio 4.

Y finalmente, ubicamos el punto exacto, exigiendo que el ángulo formado entre el vector del módulo y el eje X sea de 45 grados, tal como nos dice el argumento.

Y así representamos un número complejo en forma trigonométrica.

Ejercicio del plano complejo

Para acabar con esta publicación, te vamos a plantear un ejercicio final. Te recomendamos mucho que lo resuelvas, porque así consolidarás los conocimientos explicados a lo largo de este artículo.

Prueba de graficar los siguientes tres números complejos en el plano complejo:

z = 2 – i

w = √2₁₈₀

p = cos (60) + i · sen(60)

Más sobre el plano complejo

• Números complejos
• Números imaginarios

En este artículo vamos a tratar las propiedades de los números complejos, las cuales nos pueden venir bien a la hora de resolver cálculos y simplificar expresiones. Vamos directos a ver estas propiedades.

Módulo y argumento de un número complejo

La primera propiedad de un número complejo es el módulo y el argumento de un número complejo. Esto es muy fácil de calcular, pues sencillamente hay que aplicar un par de fórmulas.

La fórmula para calcular el módulo:

La fórmula para calcular el argumento:

Ahora bien, si el número está expresado en forma polar o trigonométrica, no hace falta hacer ningún cálculo. Porque, en la misma expresión, se detallan tanto el módulo como el argumento.

En la siguiente imagen, puedes ver la fórmula de un número en forma polar, donde |z| es el módulo y α es el argumento.

Y en esta otra imagen, puedes ver la estructura de un número expresado en forma trigonométrica, donde |z| es el módulo y α es el argumento.

Números complejos iguales

Los números complejos iguales son aquellos que comparten módulo y argumento. Por lo tanto, partiendo de estos dos valores:

Estos son iguales si se cumple la siguiente propiedad.

Por otro lado, si tenemos ambos números en forma binómica, podemos hacer una comprobación muy rápida y sencilla para saber si son dos números complejos iguales. Sencillamente, se debe cumplir la siguiente expresión:

a + bi = a + bi

Vamos a ver un ejemplo, determina si los dos números complejos siguientes son iguales:

Números complejos conjugados

Ahora pasamos a una de las propiedades más importantes de los números complejos, pues saber calcular el conjugado de un complejo nos ayuda mucho a resolver divisiones complejas y a hacer simplificaciones.

Entonces, partiendo de estos dos valores:

Decimos que son conjugados si comparten módulo y tienen argumentos opuestos. Por lo tanto, debe cumplirse:

Por otro lado, si tenemos ambos números en forma binómica, podemos hacer una verificación muy rápida y sencilla para saber si son dos números complejos conjugados. Sencillamente, se debe cumplir la siguiente expresión:

a + bi = a – bi

Vamos a ver un ejemplo, determina si los dos números complejos siguientes son conjugados:

Números complejos opuestos

A continuación, pasamos a ver la propiedad de los números complejos opuestos. Partiendo de estos dos valores:

Podemos decir que son opuestos si tienen mismo módulo y sus argumentos difieren 180 grados o π radianes:

Por otro lado, si tenemos ambos números en forma binómica, podemos otro método aún más rápido y sencillo para saber si son dos números complejos opuestos. Sencillamente, se debe cumplir la siguiente expresión:

a + bi = -a – bi

Vamos a ver un ejemplo, determina si los dos números complejos siguientes son opuestos:

Otras propiedades

Evidentemente, este conjunto numérico tiene otras propiedades, como por ejemplo, los números complejos inversos y algunas otras que están relacionadas directamente con las operaciones aritméticas básicas. Aunque, todas estas las comentamos en otros artículos, los cuales puedes ver en la lista de abajo.

Más sobre las propiedades de los números complejos

• Números complejos
• Operaciones con números complejos
• Raíces complejas
• Representación gráfica de los números complejos