Cómo factorizar polinomios

¿Qué es la factorización de polinomios? Es una técnica matemática que permite descomponer un polinomio en factores o expresiones más simples. Y gracias a esta simplificación, podremos realizar operaciones entre múltiples expresiones algebraicas de manera más fácil y cómoda. Entonces, a lo largo de este artículo te comentaremos diferentes métodos para factorizar polinomios y todos los casos posibles de factorización.

¿Cómo factorizar un polinomio?

Existen muchos métodos de factorización los cuales tienen una estructura de resolución propia, pero que al final se basa en lo mismo. Además, también te puedes encontrar con una gran variedad de casos en cuanto a la configuración del polinomio. Es por eso que en los siguientes apartados te comentaremos todos los procedimientos que existen y cuándo usar cada uno. Finalmente, lo aplicaremos a un ejemplo real para que acabes de adquirir los conceptos.

Factorizar un polinomio con la regla de Ruffini

El método más usado para factorizar polinomios es la regla de Ruffini, ya que es fácil de usar y además el resultado se puede hallar de manera rápida. Lo normal es usar esta técnica para la factorización de polinomios de grado superior a dos, o a veces incluso para factorizar polinomios de segundo grado. Puesto que te permite obtener las raíces de ese polinomio muy gráficamente. Aunque este uso lo explicaremos en el siguiente apartado el cual se centra en las raíces de una expresión matemática de este tipo.

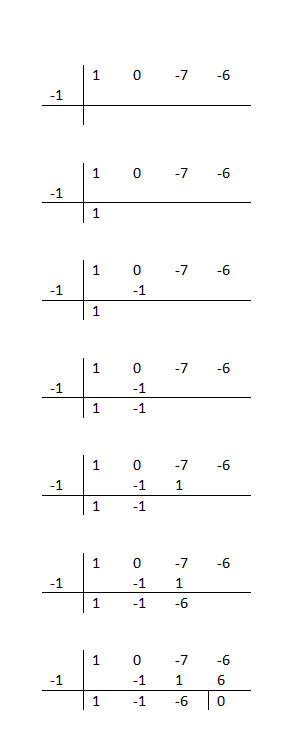
¿Cómo hacer Ruffini para factorizar polinomios?

Básicamente, deberemos escribir los coeficientes del dividendo en una fila horizontal y el valor de una posible raíz del polinomio en el lateral. Decimos posible, porque deberemos buscar un divisor que permita obtener un residuo igual a cero. De lo contrario, ese número no será una raíz válida y deberás seguir probando.

A modo de truco te recomendamos que pruebes solamente números divisores del término independiente (último valor de la fila horizontal). Entonces, para poder saber si es correcto el número que has escogido, simplemente deberás seguir la secuencia de cálculos siguiente:

Bajas el coeficiente, lo multiplicas por la raíz que estás probando, lo escribes debajo del siguiente coeficiente y haces una suma en vertical. Solamente tendrás que repetir estos pasos hasta llegar al final, y una vez hayas terminado sabrás si ese valor es correcto o no. Ya que únicamente serán válidos los números que den un residuo nulo.

Si no te ha quedado muy claro el procedimiento matemático que debes seguir, puedes fijarte en el ejemplo de la columna que hay a la izquierda de este texto. Además, te recomendamos que pruebes a factorizar el siguiente polinomio: x³ + 2x² – x – 2 (basándote en el ejemplo). Y finalmente para saber si has resuelto bien el ejercicio o no, podrás comparar tu resultado con este:

• Expresión sobrante = x² + 3x + 2
• Residuo = 0

Ahora haremos una breve explicación sobre la aplicación de Ruffini en la factorización. Aunque si quieres saber cómo se usa este recurso matemático de manera detallada, te recomendamos que accedas al último artículo que hemos enlazado, ya que allí está todo muy bien explicado. Dicho esto empecemos a explicar cómo factorizar polinomios con la regla de Ruffini:

• Dibujamos la cuadrícula: tal como se puede apreciar en la imagen de arriba crearemos un recuadro en el cual haremos el Ruffini. Básicamente, deberemos escribir los coeficientes de la expresión ordenados en horizontal y sin dejarnos los que tengan un valor nulo. Al final debería quedarte una representación similar a la de la imagen pero con los valores de tu polinomio.
• Calculamos las raíces: una vez tengamos dibujada la estructura y nos hayamos asegurado de que tenemos bien escritos todos los números, entonces procederemos al cálculo de la raíz. Deberás encontrar las raíces siguiendo la secuencia de cálculo que hemos comentado justo encima de esta lista (junto con las imágenes).
• Expresamos la raíz en forma (x – a): cuando tengamos todas las raíces del polinomio entonces deberemos expresarlas en el siguiente formato (x – a). Teniendo en cuenta que a son los valores que hemos obtenido, por ejemplo si hemos extraído como resultado x = 2, x = -2 y x = 4, entonces obtendremos (x – 2), (x + 2) y (x – 4).
• Juntamos todos los factores en una sola expresión: por último cuando tengamos ya todas las raíces expresadas en el formato correcto, simplemente nos quedará juntarlas en una sola expresión algebraica. Siguiendo con el anterior ejemplo, nos quedaría algo así: (x – 2) · (x + 2) · (x – 4).

Factorizar un polinomio usando las raíces de un polinomio

El concepto de raíz de un polinomio lo hemos explicado a medias en el apartado de Ruffini. Pero, la definición exacta sería: la raíz de un polinomio P(x) es un valor numérico a, tal que P(a) = 0. Por lo tanto, se trata de un número capaz de anular la función o el polinomio en cuestión. A modo de resumen podríamos decir que sirve para descomponer un polinomio en el producto de factores.

Por ejemplo, si nos dan la siguiente expresión x² − x − 2 y la factorizamos ya sea mediante la regla de Ruffini o simplemente resolviendo la ecuación de segundo grado x² − x − 2 = 0. Obtendremos dos valores x = -1 y x = 2, con lo cual si los cambiamos al formato (x – a) y los juntamos, llegaremos a la siguiente expresión: (x + 1) (x − 2), es decir el polinomio factorizado. Y esto lo podemos aplicar a polinomios de grado superior a dos, aunque la expresión estaría formada por más términos.

Factorizar un polinomio por extracción de factor común

Cuando queremos factorizar polinomios sin término independiente o expresiones que tienen un factor común en todos los términos, entonces podemos simplificar el polinomio por medio de esta técnica. Básicamente consiste en aplicar la propiedad distributiva a toda la expresión, sacando ese factor común que se repite y añadiéndolo multiplicando a todo el polinomio. A continuación puedes encontrar un ejemplo del primer caso que hemos comentado (polinomio sin término independiente):

2x³ + 10x² – 6x = 2x (x² + 5x – 3)

Doble extracción de factor común

La extracción de factor común se puede hacer hasta extrayendo factores más complejos, los cuales incluyen múltiples variables. E incluso puedes llegar a extraer polinomios derivados de la propia expresión principal. Es importante no ponerse límites cuando quieras realizar este tipo de operación, ya que el objetivo de extraer factores es simplificar al máximo una expresión algebraica.

Factorización de polinomios mediante identidades notables

Los productos notables pueden ayudarnos a factorizar expresiones polinómicas, ya que son una especie de expresiones algebraicas simplificadas. Por lo tanto, nos ayudan a pasar directamente de un polinomio extenso a una pequeña fórmula compuesta por pocos términos. Así que es bastante recomendable aprenderse las fórmulas de las identidades notables para poder identificar rápidamente cuándo podemos usarlas. Y como resultado, ahorrarnos tiempo factorizando con Ruffini o alguno de los otros métodos. A continuación, comentaremos las tres normas que debes aprenderte:

• Diferencia de cuadrados: a² – b² = (a + b) · (a – b)
• Cuadrado de la suma: a² + 2ab + b² = (a + b)²
• Cuadrado de la resta: a² – 2ab + b² = (a – b)²

Factorización de polinomios por agrupación

En contados casos podemos encontrarnos con un polinomio de estructura x² – ax – bx + ab, el cual se puede simplificar sacando factor común: x (x – a) – b (x – a). Y si volvemos a sacar factor común aún se puede simplificar más: (x – a) · (x – b). Por lo tanto, las raíces de este polinomio serían x = a y x = b. Como se puede ver este tipo de expresión algebraica tiene una estructura muy fácil de factorizar y operar.

Ejercicios de factorización de polinomios

Por último, queremos facilitarte una serie de ejercicios para que practiques la factorización de polinomios. De esta manera, podrás interiorizar mejor la teoría que hemos explicado hoy. Simplemente, deberás resolver los ejercicios en tu cuaderno y después comparar los resultados con los que te ofrecemos a continuación.

• x⁴ -1 = (x² + 1) (x + 1) (x – 1)
• x⁵ + x⁴ – x – 1 = (x – 1) (x + 1)² (x² + 1)
• 9x² + 30x + 25 = (3x + 5)²
• x⁴ – 3x³ – 3x² + 11x – 6 = (x + 2) (x – 3) (x – 1)²