Demostración y aplicación de la fórmula de Euler

La fórmula de Euler es un concepto matemático que relaciona dos conceptos elementales de las matemáticas: los números complejos y la trigonometría. Esto lo convierte en una de las conceptualizaciones más importantes y con más aplicaciones de toda la matemática. A lo largo de este artículo veremos cómo es esta fórmula y todos los usos que tiene.

¿Qué es la fórmula de Euler?

La fórmula de Euler es una ecuación matemática fundamental basada en el número de Euler, la cual relaciona los números complejos con la trigonometría. Fue descubierta por el matemático suizo Leonhard Euler en el siglo XVIII y desde entonces ha sido utilizada en una variedad de campos, desde la física hasta la informática.

La fórmula de Euler se escribe como e^ix = cos(x) + i · sen(x), donde e es la base del logaritmo natural, i es la unidad imaginaria (definida como la raíz cuadrada de -1) y x es un número real. Esta ecuación especifica que el número complejo e^ix es igual a la suma del número real cos(x) y del producto del número imaginario i por el número real sen(x).

La importancia de la fórmula de Euler radica en que permite expresar los números complejos en términos de números reales y trigonometría, lo que facilita su manejo y cálculo.

Demostración de la fórmula de Euler

La demostración de la fórmula de Euler se basa en el uso de la serie de Taylor para la función exponencial y la identidad trigonométrica para coseno y seno.

Primero, consideramos la serie de Taylor para la función exponencial:

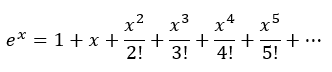
Luego, reemplazamos x por ix en la ecuación anterior, donde i es la unidad imaginaria (raíz cuadrada de -1):

Entonces, aplicamos las potencias de i y reemplazamos en la ecuación anterior:

Ahora, agrupamos los términos reales y los términos con i:

En realidad, cada uno de los paréntesis anteriores son la serie de Taylor para coseno y seno:

Finalmente, simplificamos (sustituyendo cada expresión de los paréntesis por coseno y seno de x) y logramos:

Ejemplo de la fórmula de Euler

Ahora que ya sabes cómo funciona esta fórmula matemática, te recomendamos que pruebes de resolver el siguiente ejemplo resuelto: Expresa el número complejo e²ⁱ (en radianes) en forma binómica:

La principal aplicación de la fórmula de Euler es convertir un número complejo expresado en forma exponencial, a forma binómica. Por lo tanto, vamos a usar la fórmula: e^ix = cos(x) + i · sen(x)

e²ⁱ = cos(2) + i · sen(2)

e²ⁱ = -0,416 + 0,909i

Y ya tendríamos el número en forma binómica. A partir de aquí podemos hacer la representación gráfica en el plano complejo. Para hacerlo, hay que entender que un número complejo se representa en el plano complejo usando como coordenadas la parte real en las abscisas (eje de las x) y la parte imaginaria en las ordenadas (eje de las y).

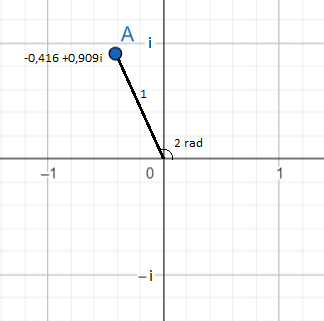
En la anterior imagen queda representado el número complejo e²ⁱ, que es igual a -0,416 + 0,909i. Este se puede ver como un punto de color azul. Podemos ver su localización en el plano a partir de dos perspectivas.

La primera y más obvia es con la representación del número en forma binómica: -0,416 (en el eje de las x) y 0,909 (en el eje de las y). Y la segunda es a partir de la forma exponencial: el módulo de e²ⁱ es igual a 1, porque es el número que hay delante de la e (como no hay ningún número delante de e, debemos imaginar que hay un 1) y en el exponente hay un 2, por lo tanto, el argumento o ángulo es equivalente a dos radianes.

Si no acabas de entender este último párrafo, te recomendamos que leas nuestro artículo sobre números complejos. Pues allí hacemos una explicación muy profunda sobre las diferentes formas de escribir un número complejo y todas sus propiedades.

Representación gráfica de la fórmula de Euler

En el ejemplo anterior has podido ver cómo se aplica la fórmula de Euler y cómo se representa gráficamente en el plano complejo. Pero, si vamos un poco más allá y tratamos de representar una función equivalente a la fórmula de Euler, nos encontramos con algo muy curioso: genera un círculo de radio 1:

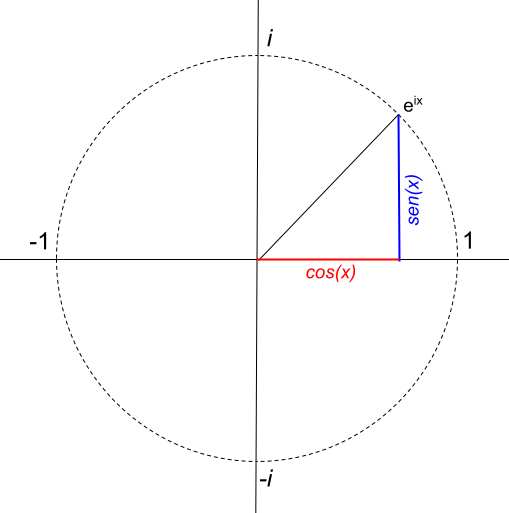
Aunque, el radio del círculo depende directamente del valor del módulo del número complejo. Por ejemplo, si queremos representar un círculo de radio 4, la función será 4e^ix. De modo que, la función 4e^ix, queda representada así:

Volviendo a la circunferencia de radio 1, si decidimos representar e^iπ (en radianes), debemos calcular primero:

e^πi = cos(π) + i · sen(π)

e^πi = -1 + i · 0

e^πi = -1

Obtenemos e^πi = -1, que es la famosa identidad de Euler.

A partir de aquí deducimos que el número complejo e^πi solamente tiene parte real, la cual es igual a -1. Por lo tanto, su representación quedaría tal que así:

Aplicaciones de la fórmula de Euler

1. Números complejos: la fórmula de Euler es una relación entre las funciones trigonométricas y los números complejos. A partir de esta fórmula podemos expresar los números complejos de diferentes formas: binómica, exponencial y polar.
2. Series de Taylor: la fórmula de Euler se utiliza para expandir funciones en series de Taylor.
3. Álgebra lineal: la fórmula de Euler se usa en la diagonalización de matrices, lo cual es una técnica fundamental en álgebra lineal.
4. Cálculo diferencial e integral: la fórmula de Euler se emplea en la solución de ecuaciones diferenciales, lo cual es una técnica relevante en cálculo.

Además, tiene aplicaciones en muchas teorías matemáticas e incluso, en conceptos que quedan fuera del ámbito matemático, como por ejemplo en teoremas de física.

Conclusiones

Como habrás podido ver en este artículo, la mayor aplicación de la fórmula de Euler es en los números complejos: en su expresión numérica y en su representación. Es cierto que tiene alguna aplicación en el álgebra, pero esencialmente, se trabaja con los números complejos. Así que es importante entenderlos bien, antes que nada.

Dicho esto, esperamos haberte ayudado a entender mejor este concepto. Y si te ha quedado alguna pregunta o no sabes cómo proceder con algún ejercicio, no dudes en escribirnos en los comentarios.