Seguro que has oído hablar de los números complejos. Son quizás el conjunto numérico más difícil de tratar, pues combinan los números reales y los imaginarios. Su unificación nos permite estudiar comportamientos numéricos que no se pueden tratar desde el conjunto de los reales.
Contenido
¿Qué son los números complejos?
Los números complejos son la combinación de un número real y un número imaginario. Por ejemplo, 4 + 5i es un número complejo que tiene una parte real equivalente a 4 y una parte imaginaria igual a 5i. De forma general, podemos expresarlos a través de la siguiente fórmula:
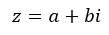
Donde, Re(z) = a y Im(z) = b
Como bien hemos dicho, los complejos son el conjunto mayor o global, el cual comprende tanto los números reales como los números imaginarios. A continuación, te mostramos un pequeño esquema sobre la estructura jerárquica de todos los conjuntos:

Por lo tanto, cuando tenemos una combinación de un número real y uno imaginario, tenemos un número complejo. Pero, hay veces que una de las dos partes es igual a cero. ¿Qué pasa en estos casos? Pues bien, seguimos tratando con complejos, porque el conjunto complejo abarca todos los otros conjuntos numéricos. Pero, entramos en una subcategoría diferente:
| Número Complejo | Parte Real | Parte Imaginaria | Subcategoría |
| 2 + 5i | 2 | 5i | Complejo |
| 4 | 4 | 0 | Real Puro |
| 3i | 0 | 3i | Imaginario Puro |
Cuando tenemos un real puro, como el valor imaginario b es igual a cero, el número complejo que queda es equivalente a:
z = a + 0i = a
Por otro lado, cuando tenemos un imaginario puro, la a es igual a cero y, por lo tanto, el número complejo queda tal que así:
z = 0 + bi = bi
Representación gráfica de los números complejos
Para representar los números complejos, usamos el plano complejo. El cual está formado por dos rectas: la recta real y la recta imaginaria. Estas dos rectas numéricas se utilizan para situar gráficamente los números de cada conjunto y si las juntamos, obtenemos un plano, tal que así:
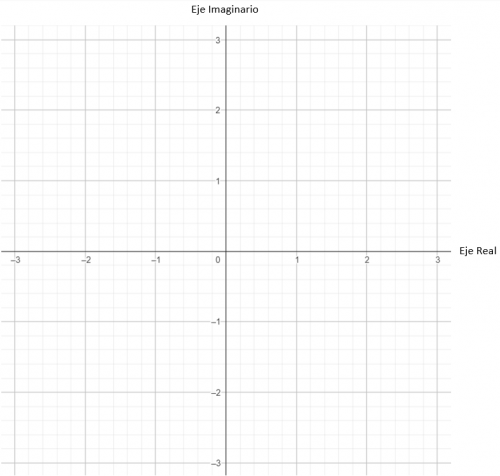
El eje X, se llama eje real porque es donde se sitúan los valores de la parte real. Mientras que el eje Y se llama eje imaginario, y es donde se escriben los valores imaginarios. Vamos a ver un ejemplo, situaremos en el plano complejo el número 3 + 2i.
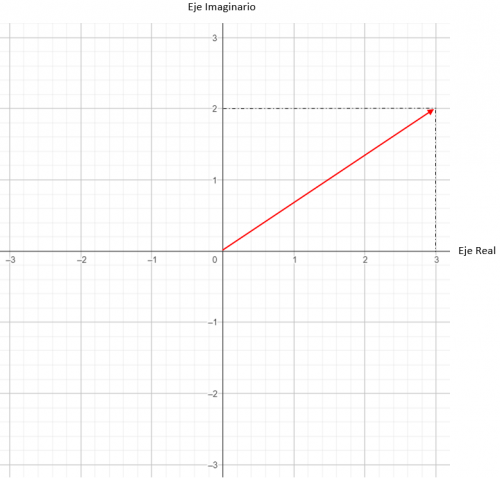
Como has podido ver en la imagen, hemos situado el número utilizando como coordenadas los números 3 y 2, cada uno para un eje. Si quieres saber más sobre cómo representar números complejos, te recomendamos que te leas este artículo.
¿Cuáles son los tipos de los números complejos?
Ahora, vamos a ver las formas que tenemos de expresar un número complejo. Hasta el momento, solamente hemos visto la forma base (conocida como forma binómica), la cual se escribe como una suma: parte real más parte imaginaria.
Pero, en realidad, tenemos tres formas: la binómica, la polar y la trigonométrica. Cada tipo de expresión, tiene sus propiedades, y se usa en una situación u otra. Así que, vamos a explicarlas todas y a mostrar cómo se pasa de una a otra.
1. Forma binómica
Los números complejos en forma binómica se escriben como la suma de la parte real más la parte imaginaria: a + bi. Por ejemplo, el número 6 + i, es un complejo expresado en notación binómica. En este, la fórmula siempre es la misma:
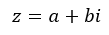
En consecuencia, para expresar un número complejo en forma binómica, solamente nos hace falta conocer su valor real y su valor imaginario.
Por ejemplo, el valor 3 + 2i está en forma binómica y como hemos visto antes, queda representado tal que así:

La forma binómica se emplea mayormente para resolver sumas y restas de números complejos.
2. Forma polar
Para expresar los números complejos en forma polar, debemos calcular su módulo |z| y su argumento. La forma polar se utiliza mayormente cuando debemos resolver multiplicaciones y divisiones de números complejos.
Para calcular el módulo del número complejo, solamente tenemos que hacer el módulo de a y b, tal como se explica en la siguiente fórmula:

Y para calcular el argumento o ángulo de z, tenemos que calcular el arcotangente de b entre a:

Es importante destacar, que para determinar exactamente el valor del ángulo α, es necesario ubicar en qué cuadrante se encuentra. Lo cual se debe a que la función arcotangente solamente calcula ángulos entre π/2 y -π/2. Para concretar en qué cuadrante está situado el número complejo, debemos fijarnos en los valores a y b (si son positivos o negativos):
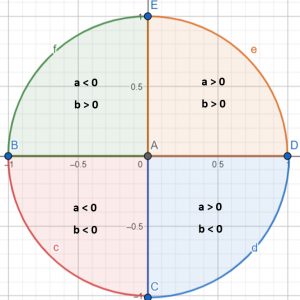
Una vez sabemos en qué cuadrante está situado nuestro número, debemos seguir unas normas:
- Si el número complejo está en el primer cuadrante (a > 0 y b > 0), dejaremos el argumento tal como está.
- Si el número complejo está en el segundo cuadrante (a < 0 y b > 0), sumaremos π al argumento.
- Si el número complejo está en el tercer cuadrante (a < 0 y b < 0), restaremos π al argumento.
- Si el número complejo está en el cuarto cuadrante (a > 0 y b < 0), sumaremos 2π al argumento.
En el caso de que no sepas a lo que nos referimos cuando decimos cuadrante, te recomendamos que visites nuestro artículo sobre las razones trigonométricas.
Una vez conocemos el módulo y el argumento de z, podemos expresar el número complejo en forma polar. Aunque, esta forma acepta varias nomenclaturas, las dos principales son:
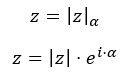
Por ejemplo, si queremos pasar el número 3 + 5i a polar, sencillamente debemos seguir el siguiente procedimiento.
Primero, calculamos el módulo:
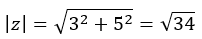
Después, calculamos el argumento, el cual está en el primer cuadrante, así que se queda tal cual lo hemos calculado.
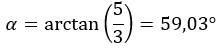
Y expresamos el número en forma polar:
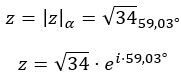
Su representación gráfica queda tal que así:

3. Forma trigonométrica
Por último, tenemos la notación trigonométrica, la cual se calcula a partir de la fórmula de Euler:
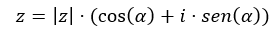
Por ejemplo, para expresar el número 4 – 3i en forma trigonométrica, seguimos el siguiente procedimiento:
Empezamos por calcular el módulo y el argumento con las fórmulas que hemos empleado en el apartado de la forma polar.

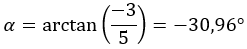
ATENCIÓN: El argumento está en el cuarto cuadrante, porque (a > 0 y b < 0).
Añadimos los datos en la ecuación de la forma trigonométrica.
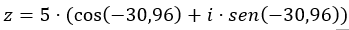
Y ya tenemos expresado el número en forma trigonométrica. Su representación gráfica es la siguiente.
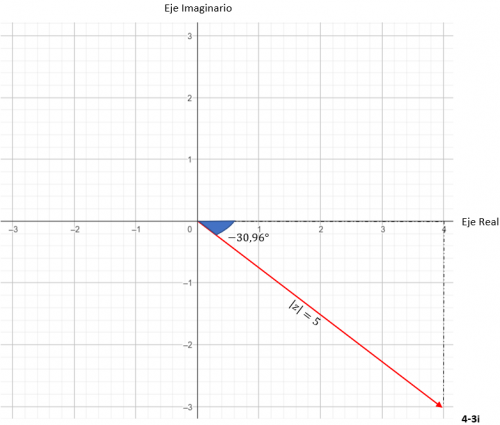
¿Cómo pasar de un tipo a otro?
Ahora ya conoces todas las formas de expresar un número complejo. Y a lo largo del último apartado has podido ver cómo se llega hasta cada una de ellas, pero antes de acabar, queremos hacer un pequeño resumen sobre cómo se pasa de una forma a otra. Solamente, hay que usar las fórmulas que hemos visto en el anterior apartado.
De forma binómica a forma polar y viceversa
Para pasar de binómica a polar, te planteamos el siguiente esquema:

Antes hemos visto un ejemplo en el que pasamos de binómica a polar, así que ahora vamos a pasar de polar a binómica utilizando el esquema de arriba. Tenemos que convertir √4138,66 a binómica.
Primero calculamos la a.
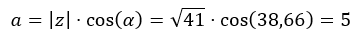
Seguidamente calculamos la b.
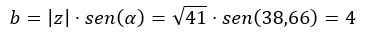
Y lo expresamos en forma binómica.
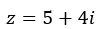
La representación gráfica de este número queda así:
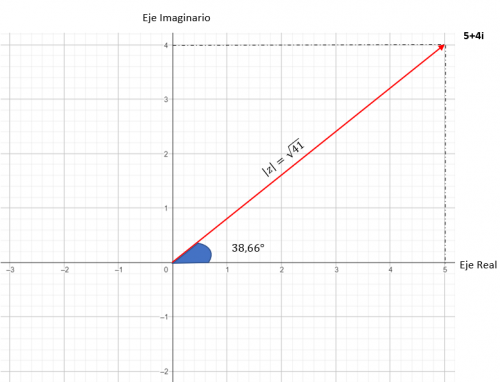
De forma binómica a forma trigonométrica y viceversa
Para pasar de binómica a trigonométrica, también debemos aplicar las fórmulas que hemos comentado en el anterior apartado. De esta forma, primero calculamos el módulo y el argumento, y después ponemos esos datos en la ecuación de la forma trigonométrica. Por poner un ejemplo, vamos a pasar el número z = 3 + 2i a trigonométrica.
Primero calculamos el módulo y el argumento.
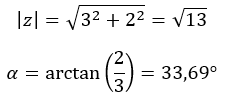
ATENCIÓN: El argumento está en el primer cuadrante, porque (a > 0 y b > 0).
Después, completamos la ecuación de la forma trigonométrica con estos datos.

Y si queremos pasar de trigonométrica a binómica, sencillamente debemos resolver la expresión anterior.

De forma polar a forma trigonométrica y viceversa
Por último, vamos a pasar de forma polar a trigonométrica. Lo cual es algo muy sencillo, porque estas dos formas se expresan mediante los mismos dos valores: módulo y argumento. Así que solamente hay que rellenar las fórmulas y ya está.
Pongamos un ejemplo, vamos a convertir el número z = √8512,53 a forma trigonométrica.
Replanteamos las dos variables (módulo y argumento) en la ecuación de la forma trigonométrica:
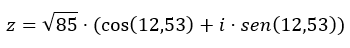
Así que ahora ya sabes cómo pasar de una forma a otra, te recomendamos que practiques un poco con algunos ejercicios. De esta manera, consolidarás los conocimientos aprendidos en este artículo. Si tienes alguna pregunta referente a este tema, no dudes en dejarla en los comentarios. Y si quieres leer más sobre números complejos, mírate los enlaces de abajo.