La notación matemática es una forma de comunicar ideas y cálculos mediante el uso de símbolos. Aunque a primera vista puede parecer confusa, con un poco de práctica podrás interpretarla con facilidad. En este artículo, te mostraremos los significados de todos símbolos que se emplean en esta notación y algunos ejemplos de cómo aplicarlos.
Contenido
¿Qué es la notación matemática?
La notación matemática es una forma de escribir los valores y expresiones que se usan en las matemáticas. Esta técnica permite a los matemáticos manifestar ideas de forma concisa y precisa. La notación matemática también hace que sea más fácil comprender los conceptos con una mayor claridad, para los que practican o estudian las matemáticas.
No debes confundir el lenguaje matemático con la notación científica, que es una manera de escribir valores numéricos. Mientras que la notación matemática es más bien un conjunto de símbolos que permiten escribir expresiones complejas, igual que una lengua. Más adelante entraremos en más detalle acerca de este tema.
¿Cómo se lee la notación matemática?
Aprender a interpretar la notación matemática es más fácil de lo que parece, solamente hay que aprenderse el significado de cada símbolo y una vez que lo hagas, podrás leer cualquier cosa que esté escrita en notación matemática. Es así de fácil, aunque evidentemente requiere de práctica y mucho tiempo de estudio.
Las expresiones matemáticas son muy lógicas y siempre siguen patrones, por lo tanto, solo debes memorizarte las normas y después, sabrás extrapolarlas a cualquier situación. Incluso podremos llegar a describir cálculos muy complejos, esta es la magia del lenguaje matemático, que nos permiten comunicar mensajes muy elaborados de una manera metódica.
Componentes de la notación matemática
La notación matemática se compone de una serie de símbolos que representan a los números, las operaciones y las relaciones entre ellos. Estos símbolos pueden parecer complicados al principio, pero con un poco de práctica y comprensión, interpretar la notación matemática te resultará de lo más fácil.
A continuación, te explicaremos en gran detalle los cuatro tipos de elementos que nos podemos encontrar en el lenguaje matemático. Empezando por los más básicos y acabando por los más complejos y abstractos. Y una vez acabada la explicación teórica, hablaremos sobre los tipos de notaciones numéricas que existen.
Números y conjuntos numéricos
En primera instancia, debemos definir los números matemáticos, estos son un concepto matemático que designa una cantidad en consonancia con una unidad. Podemos describir cualquier valor numérico, siguiendo el sistema de numeración decimal y combinando los siguientes símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9.
Si ordenamos los números según diferentes propiedades, obtenemos varias categorías numéricas, que se conocen como conjuntos numéricos. Y estos grupos de valores, también tienen símbolos propios que los designan, en la siguiente lista te los presentamos todos con el nombre del grupo correspondiente:
- ℙ: Números primos
- ℕ: Números naturales
- ℤ: Números enteros
- ℚ: Números racionales
- ℝ: Números reales
- 𝕀: Números imaginarios
- ℂ: Números complejos
- ℍ: Cuaterniones
Estos símbolos se suelen emplear en nuestros cálculos, para determinar un gran abanico de números, de una tirada. Por ejemplo, si tenemos una expresión que acepta muchos valores como resultado, en vez de escribir los números uno por uno, nos será más fácil explicitar estos valores a través del símbolo correspondiente a su grupo numérico.
Operadores y cuantificadores
Ahora que ya hemos comentado los números, que son la esencia de las matemáticas, debemos hablar sobre los operadores y los cuantificadores. Los primeros son todos aquellos símbolos que nos permiten representar una operación: suma (+), resta (-), multiplicación (x o ·), división (÷), entre otros.
Aunque, también tenemos dos otros tipos de operadores, que son los operadores lógicos y los operadores de relación. Los primeros expresan conjunción, disyunción y negación. Nos sirven para plantear operaciones lógicas, que a diferencia de las operaciones aritméticas, no trabajan con números, sino con proposiciones matemáticas.
Mientras que los segundos, nos permiten establecer equivalencias y relaciones entre valores o expresiones matemáticas. Estos símbolos pueden usarse en los cálculos aritméticos (para ordenar números), pero tienen más importancia en el álgebra, cuando tenemos variables (más sobre esto dentro de dos apartados).
En la siguiente lista, puedes encontrar la definición de todos los operadores que hemos comentado hasta ahora:
| Símbolo | Definición | Tipo |
| + | Suma | Operador aritmético |
| – | Resta | Operador aritmético |
| x, *, · | Multiplicación | Operador aritmético |
| ÷ | División | Operador aritmético |
| x² | Potenciación | Operador aritmético |
| √ | Radicación | Operador aritmético |
| Y | Conjunción | Operador lógico |
| O | Disyunción | Operador lógico |
| NO | Negación | Operador lógico |
| = | Igual a | Operador de relación |
| > | Mayor que | Operador de relación |
| < | Menor que | Operador de relación |
| >= | Mayor o igual que | Operador de relación |
| <= | Menor o igual que | Operador de relación |
| ≠ | No es igual a | Operador de relación |
| ≡ | Exactamente igual | Operador de relación |
| ≈ | Aproximadamente igual | Operador de relación |
| ≃ | Equivalente a | Operador de relación |
| ∝ | Proporcional | Operador de relación |
Aunque, también hay cinco operadores lógicos más, que se usan para explicar la lógica matemática desde la teoría de conjuntos. Que es una rama que aplica la lógica de conjuntos, lo cual se usa en cálculo, geometría, estadística… A continuación, te mostramos los símbolos que se emplean y su definición.
| Símbolo | Definición |
| x ∈ A | x pertenece a A |
| x ∉ A | x no pertenece a A |
| ∪ | Unión |
| ∩ | Intersección |
| ⊂ | Inclusión |
En cuanto a los cuantificadores, podemos definirlos como unos símbolos que nos indican la cantidad de elementos de un conjunto que cumplen con una determinada condición (equivalencia, orden, pertenencia, etc.). Hay una gran variedad de operadores, pero entre los más usados, podemos destacar:
| Símbolo | Definición | Tipo |
| ∀x | Para todo x | Cuantificador |
| ∃x | Existe por lo menos un x | Cuantificador |
| ∄x | No existe un x | Cuantificador |
| ∃!x | Existe un único x | Cuantificador |
| | | Tal que | Cuantificador |
| ∴ | Por lo tanto | Cuantificador |
Expresiones matemáticas y sus relaciones
Con los símbolos que hemos tratado hasta ahora, puedes entender una gran parte de las matemáticas, pero aún no hemos explicado sus aplicaciones o relaciones en expresiones complejas, como las operaciones combinadas o el cálculo algebraico. Además, todavía quedan los símbolos de relación por comentar. Estos son los que veremos en este apartado.
Empezando por los símbolos de agrupación, estos son los paréntesis, los corchetes y las llaves. Estos elementos son clave en la designación de fórmulas complejas. Su principal función es dar prioridad a ciertos cálculos, dentro de una expresión global. Y hay diferentes niveles de prioridad entre los tres tipos. En esta expresión puedes ver el orden de escritura 3 {[2 + (3 – 2) · 2] – 4}.
| Símbolos | Definición | Prioridad |
| «(» y «)» | Paréntesis | Máxima prioridad |
| «[» y «]» | Corchetes | Segunda prioridad |
| «{» y «}» | Llaves | Tercera prioridad |
Y para terminar esta categoría, hablaremos sobre los sumatorios (Σ) y los productos (∏), que son elementos que nos permiten describir sumas y multiplicaciones que se repiten. El sumatorio equivale a decir: «suma de Xi, donde i toma los valores de 1 a n». Y el producto es lo mismo, pero en vez de sumar, hacemos multiplicaciones.
Análisis algebraico
El primer elemento que hay que tratar sobre los símbolos algebraicos son las variables, que se representan mediante las letras del alfabeto. Su función es la de imitar a un número, pero no tienen un valor fijo como las constantes matemáticas, por lo tanto, pueden adoptar nuevos valores. Esto se aplica en las ecuaciones, los límites, las derivadas, las integrales, las matrices…
Por último, queremos hablar sobre las representaciones de todas estas operaciones algebraicas que acabamos de comentar en este último párrafo. Puesto que, son la base del álgebra y hay que saber cuál es su simbología. A continuación, te mostramos una tabla con sus diferentes símbolos y una breve definición:
| Símbolo | Definición |
| limx→b | Límite (cuando x tiende a b) |
| y’, ƒ’ (x), dy / dx | Derivada |
| ∫ | Integral |
| Am x n | Matriz de dimensiones m x n |
Conclusión sobre los símbolos del lenguaje matemático
Hasta aquí has visto todos los símbolos importantes que se tratan en las matemáticas, evidentemente aún quedan algunos por comentar. Pero, estos son más específicos de cada subcategoría de las matemáticas: geometría, estadística, álgebra… Por lo tanto, vamos a cerrar este tema y a hablar de las notaciones numéricas.
Tipos de notaciones numéricas
En este apartado vamos a ver todas las formas de expresar los números matemáticos, puesto que existen diferentes notaciones para hacerlo. Al principio, hemos comentado por encima el sistema de numeración decimal, que es el más usado por los matemáticos. Seguidamente, lo explicaremos en mayor detalle y te mostraremos otros tipos de notación matemática:
Notación decimal
El sistema de numeración decimal es un sistema de numeración posicional (sistema en el cual la posición de cada dígito determinará su valor) está basado en los múltiplos y submúltiplos del número 10. Ya que el diez es el número que usa como base numérica. Por lo tanto, los diez símbolos numéricos que usaremos son los siguientes: 1, 2, 3, 4, 5, 6, 7, 8, 9 y 0.
El valor de estos números se determina a partir de la suma de los dígitos multiplicados por las potencias en base diez, establecidas en función de la posición. Y es muy importante que recuerdes que para escribir un número inferior a la unidad, deberemos usar la coma decimal. A continuación, puedes encontrar un ejemplo:
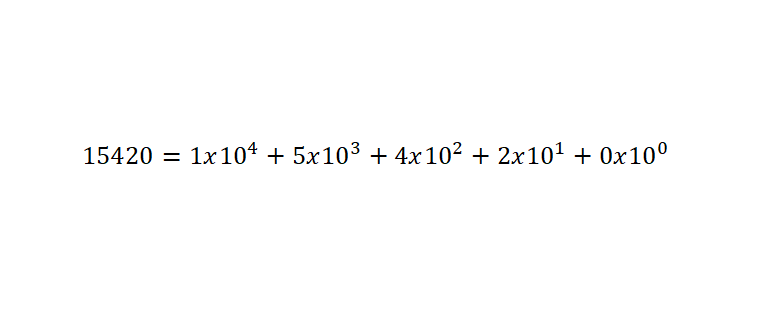
Notación científica
La notación en forma exponencial o notación científica, es claramente uno de los tipos de escritura más usados en el ámbito de la ciencia y la tecnología. Eso es debe a que nos permite expresar números muy grandes y muy pequeños de una forma simple. Para entender la definición de notación científica, vamos a explicar cómo pasar un número entero a esta notación:
- Mover la coma decimal: deberemos desplazar la coma decimal las veces que haga falta hasta llegar al primer dígito (hacia la izquierda si tenemos un número muy grande y hacia la derecha si tenemos un número muy pequeño).
- Establecer la base: escribir este último dígito multiplicado por diez, por lo tanto, junto al valor que hayas obtenido de mover la coma decimal hacia un lado, deberás escribir una multiplicación por diez: «x 10».
- Añadir un exponente: con un valor igual a la cantidad de veces que hayas movido la coma decimal. Con los números grandes vas a dejar el exponente en positivo, pero, en los números pequeños, deberás escribirlo en signo negativo.
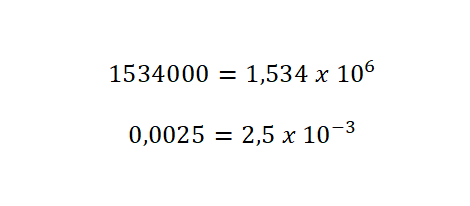
Notación hexadecimal
El sistema hexadecimal tiene como base el 16, esto quiere decir que usa dieciséis símbolos diferentes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. Como se puede ver, este sistema de numeración está formado por los números del sistema decimal y seis letras. Esta notación suele emplearse sobre todo en computación y todo lo relacionado con la informática.
Es importante aclarar que como tiene algunos símbolos en común con otros tipos de notación, siempre deberemos indicar que está escrito en hexadecimal por medio de un paréntesis y el subíndice 16. En el siguiente ejemplo puedes ver de un ejemplo muy claro la conversión de un número hexadecimal a la notación decimal:

Para poder convertir un número hexadecimal en una expresión decimal deberemos descomponer el número en sus multiplicaciones de base, tal como hemos hecho en la notación decimal, pero cambiando la base a 16. Entonces, multiplicaremos cada dígito por dieciséis elevado a la posición que ocupe ese dígito en concreto menos uno.
Notación octal
El último sistema que comentaremos es la notación octal, la cual tiene una base de 8. Esto quiere decir que solo utiliza ocho símbolos o dígitos: 0, 1, 2, 3, 4, 5, 6 y 7. Este es el sistema de numeración menos usado de todos los que hemos explicado. Cabe destacar que las conversiones de esta notación se hacen siguiendo el mismo procedimiento que las anteriores.

Notación romana
Por último, podemos hablar del sistema de numeración romano, el cual no es muy usado actualmente, pero en el pasado tuvo una gran importancia en el ámbito de las matemáticas. Puesto que fue una de las notaciones que dio la vida a las matemáticas.
Su escritura se limita a 7 símbolos: I (1), V (5), X (10), L (50), C (100), D (500) y M (1000). Y combinando estas letras se escriben todos los números. Si quieres saber cómo se combinan para dar lugar a otros números más grandes, te recomendamos que leas nuestro artículo sobre ellos, accediendo a través del último enlace.
¿Cómo se puede mejorar el rendimiento en la lectura de la notación matemática?
Existen varias formas de mejorar el rendimiento en la lectura de la notación matemática. Una forma es leer en voz alta los símbolos y números. Otra forma es familiarizarse con los símbolos y su significado. También se puede practicar la lectura de la notación matemática utilizando ejercicios y problemas.
Esperamos haberte ayudado con esta guía, por favor, si tienes alguna pregunta, no dudes en escribirla en los comentarios. O si quieres hacer alguna aportación sobre el tema, también esperamos verla en los comentarios. Dicho esto, te dejamos un artículo sobre cómo aprender matemáticas, por si quieres seguir leyendo.