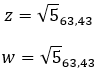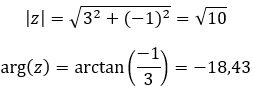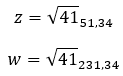En este artículo vamos a tratar las propiedades de los números complejos, las cuales nos pueden venir bien a la hora de resolver cálculos y simplificar expresiones. Vamos directos a ver estas propiedades.
Contenido
Módulo y argumento de un número complejo
La primera propiedad de un número complejo es el módulo y el argumento de un número complejo. Esto es muy fácil de calcular, pues sencillamente hay que aplicar un par de fórmulas.
La fórmula para calcular el módulo:

La fórmula para calcular el argumento:

Ahora bien, si el número está expresado en forma polar o trigonométrica, no hace falta hacer ningún cálculo. Porque, en la misma expresión, se detallan tanto el módulo como el argumento.
En la siguiente imagen, puedes ver la fórmula de un número en forma polar, donde |z| es el módulo y α es el argumento.
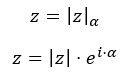
Y en esta otra imagen, puedes ver la estructura de un número expresado en forma trigonométrica, donde |z| es el módulo y α es el argumento.
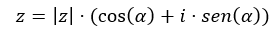
Números complejos iguales
Los números complejos iguales son aquellos que comparten módulo y argumento. Por lo tanto, partiendo de estos dos valores:

Estos son iguales si se cumple la siguiente propiedad.
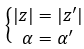
Por otro lado, si tenemos ambos números en forma binómica, podemos hacer una comprobación muy rápida y sencilla para saber si son dos números complejos iguales. Sencillamente, se debe cumplir la siguiente expresión:
a + bi = a + bi
Vamos a ver un ejemplo, determina si los dos números complejos siguientes son iguales:

Números complejos conjugados
Ahora pasamos a una de las propiedades más importantes de los números complejos, pues saber calcular el conjugado de un complejo nos ayuda mucho a resolver divisiones complejas y a hacer simplificaciones.
Entonces, partiendo de estos dos valores:

Decimos que son conjugados si comparten módulo y tienen argumentos opuestos. Por lo tanto, debe cumplirse:
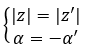
Por otro lado, si tenemos ambos números en forma binómica, podemos hacer una verificación muy rápida y sencilla para saber si son dos números complejos conjugados. Sencillamente, se debe cumplir la siguiente expresión:
a + bi = a – bi
Vamos a ver un ejemplo, determina si los dos números complejos siguientes son conjugados:
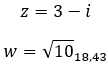
Números complejos opuestos
A continuación, pasamos a ver la propiedad de los números complejos opuestos. Partiendo de estos dos valores:

Podemos decir que son opuestos si tienen mismo módulo y sus argumentos difieren 180 grados o π radianes:
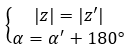
Por otro lado, si tenemos ambos números en forma binómica, podemos otro método aún más rápido y sencillo para saber si son dos números complejos opuestos. Sencillamente, se debe cumplir la siguiente expresión:
a + bi = -a – bi
Vamos a ver un ejemplo, determina si los dos números complejos siguientes son opuestos:

Otras propiedades
Evidentemente, este conjunto numérico tiene otras propiedades, como por ejemplo, los números complejos inversos y algunas otras que están relacionadas directamente con las operaciones aritméticas básicas. Aunque, todas estas las comentamos en otros artículos, los cuales puedes ver en la lista de abajo.