Las razones trigonométricas de un ángulo son las razones que se obtienen a partir de los tres lados de un triángulo rectángulo. Dicho de otro modo, son los valores que resultan de comparar por medio de cocientes (divisiones) sus tres lados. Aunque cabe destacar, que estas razones solamente existen en los triángulos rectángulos (triángulos que tienen un ángulo de 90º).
Contenido
Razones trigonométricas en un triángulo rectángulo
Las seis razones trigonométricas más importantes son: seno, coseno, tangente, cosecante, secante y cotangente. A continuación, explicaremos en gran detalle cómo se define cada una de estas razones y hablaremos sobre la fórmula que las caracteriza. Para poder entender las siguientes explicaciones tomaremos en cuenta el siguiente triángulo rectángulo:

Seno
El seno de un ángulo (sen o sin) es igual al cociente del cateto opuesto (a) entre la hipotenusa (c), por lo tanto, la fórmula del seno es la siguiente: sen (α) = a / c. Es muy importante conocer esta definición de seno, ya que, esta es la base de toda la trigonometría, al igual que las otras razones que comentaremos en este apartado.

A través del teorema del seno, podemos calcular cualquier lado del triángulo, esto lo podemos hacer relacionando los cocientes de un determinado ángulo entre su lado correspondiente. Por ejemplo, si queremos calcular el lado a y tenemos los valores del lado b y de los ángulos A y B, podemos hacerlo usando la fórmula: a / sen (A) = b / sen (B). Resolviendo esta sencilla ecuación obtenemos el valor correspondiente a la variable que queremos calcular.
Coseno
El coseno de un ángulo (cos) es igual al cociente del cateto contiguo (b) entre la hipotenusa (c), por lo tanto, la fórmula del coseno queda así: cos (α) = b / c. En este caso, la fórmula está compuesta por los dos lados del triángulo que están en contacto con el ángulo que queremos estudiar, en este ejemplo, el ángulo A o α.

Con el coseno, también tenemos una manera de calcular los lados del triángulo, que es a partir del teorema del coseno. Este nos permite relacionar los lados con los ángulos y nos ofrece las siguientes tres expresiones:
a² = b² + c² – 2bc · cos (A)
b² = a² + c² – 2ac · cos (B)
c² = a² + b² – 2ab · cos (C)
Tangente
La tercera razón más importante, con la cual cerraremos el conjunto de razones originales, es la tangente (tan o tg). Esta se calcula haciendo la división entre el cateto opuesto (a) y el cateto contiguo (b), por lo tanto, la fórmula de la tangente nos queda así: tan (α) = a / b. A continuación, puedes verlo de manera gráfica:
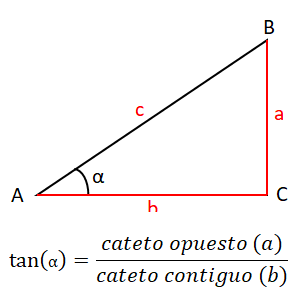
La tangente también tiene un teorema propio, el cual se llama teorema de la tangente. Este nos permite relacionar las longitudes de dos lados de un triángulo con las tangentes de los ángulos. El enunciado es el siguiente: «el cociente de la suma de dos lados entre su resta es igual al cociente entre la tangente de la media de los dos ángulos opuestos a dichos lados y la tangente de la mitad de la diferencia de estos».
Razones trigonométricas derivadas
A partir de las tres razones trigonométricas que acabamos de comentar, podemos obtener otras razones trigonométricas derivadas. Estas se obtienen al hacer la razón inversa respecto al seno, coseno y tangente.
- Cosecante: es la razón inversa del seno y se calcula con las fórmulas: cosec (α) = c / a y cosec (α) = 1 / sen (α).
- Secante: es la razón inversa del coseno y se calcula con las fórmulas: sec (α) = c / b y sec (α) = 1 / cos (α).
- Cotangente: es la razón inversa de la tangente y se calcula con las fórmulas: cotg (α) = b / a y cotg (α) = 1 / tan (α).
Tabla de razones trigonométricas
A continuación, puedes ver una tabla que resume todas las razones explicadas hasta ahora. Con esta tabla podrás memorizar de manera eficiente todas las fórmulas, ya que, permite distinguir fácilmente las diferencias entre cada expresión matemática.

Razones trigonométricas en una circunferencia
Otra manera de estudiar la trigonometría es a través de la circunferencia goniométrica o círculo unitario, esta circunferencia tiene radio igual a 1 y su origen es el punto (0, 0). El dibujo consta de un círculo y de un triángulo rectángulo representado en el interior del círculo, concretamente, el ángulo que estudiaremos tiene que estar tocando el punto de origen.
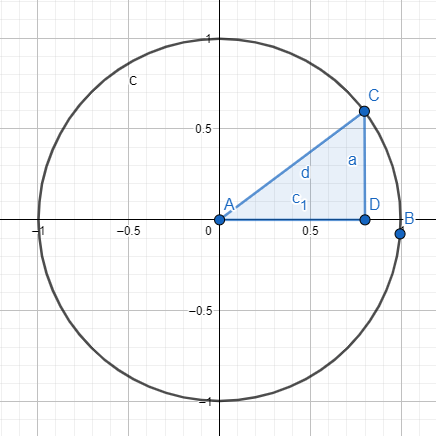
Cuando tenemos esta imagen, sabemos que el radio es igual a la hipotenusa, el cual es igual a 1. Entonces, si queremos calcular el seno y el coseno, usaremos el valor del radio y el de los otros lados del triángulo. Para calcular el seno, haremos el siguiente cálculo: sen (A) = CD / AC = CD / radio = CD / 1 = CD, por lo tanto, el seno de A es a. Por otro lado, para calcular el coseno, haremos el cálculo: cos (A) = AD / AC = AD / radio = AD / 1 = AD, como resultado, el coseno de A es c1.
Es muy importante tener en cuenta dos cosas. La primera es que el uso de este círculo en el estudio de las razones trigonométricas, se debe a la necesidad de tratar con ángulos más grandes de los que se puede estudiar con el triángulo. Por ejemplo, el ángulo de 150º no se puede estudiar a través de un simple triángulo, dado que es demasiado grande. Y la segunda cosa a tener en cuenta es que tanto el seno como el coseno, nunca podrán adoptar valores mayores al 1 y menores al -1.
Signo de las razones trigonométricas
Como ya hemos dicho antes, para tratar con ángulos más grandes que los que nos permite tratar un triángulo, usamos la circunferencia goniométrica. Para hacerlo, representamos un triángulo en el interior del círculo exactamente en uno de los cuatro cuadrantes que dividen la circunferencia, en la siguiente imagen se pueden ver representados los cuatro cuadrantes.

Entonces, para poder distinguir entre un ángulo de 30 y uno de 210, que vienen a ser lo mismo en cuanto a la distribución dentro del triángulo, usaremos una distribución de signos según el cuadrante en el que se encuentre el triángulo. A continuación, puedes ver los signos correspondientes a cada cuadrante y un ejemplo dibujado.

Por ejemplo, los ángulos de 30º y de 210º comparten el mismo valor numérico, pero su seno y su coseno tienen signo contrario. Por lo tanto: sen (30) = 1/2 y cos (30) = √3/2, mientras que sen (210) = -1/2 y cos (210) = -√3/2. Para llegar a este resultado hemos representado ambos ángulos en la circunferencia (imagen de abajo) y hemos seguido las pautas de los signos.
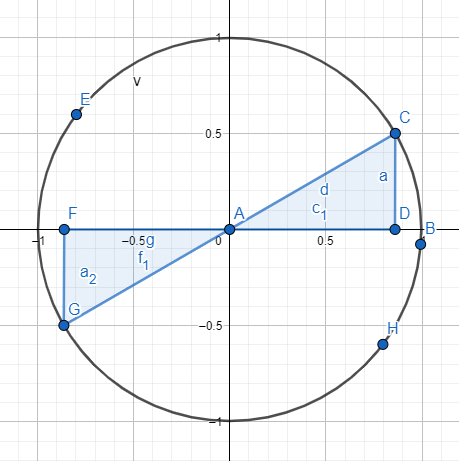
Por último, comentar que es posible tener ángulos mayores a 360º, aunque no lo parezca porque la circunferencia es de tan solo 360º. Pero, si queremos resolver un ángulo de 750º, podemos hacer una reducción a un ángulo que esté entre 0º y 360º. Sencillamente, dividimos 750 entre 360 y el resto es el ángulo que nos queda, en el caso de 750º obtenemos un ángulo de 30º.
Tipos de ángulos según el cuadrante
Existen algunas relaciones entre diferentes ángulos, las cuales nos permiten calcular las razones trigonométricas de todos los ángulos pertenecientes a la circunferencia. Nos permiten obtener esas razones a partir de la reducción al primer cuadrante. Esto que quiere decir que hacemos una simplificación de un determinado ángulo al primer cuadrante y después aplicamos los signos correspondientes. A continuación puedes encontrar los diferentes procedimientos explicados (según el cuadrante):
Primer cuadrante
En este primer cuadrante (0º – 90º) solamente tenemos que resolver la razón trigonométrica con el ángulo que nos han dado. Y si nos fijamos en la imagen que hemos explicado anteriormente sobre los símbolos, tanto el seno como el coseno tienen un positivo delante (el resultado que obtengamos no se verá afectado por el signo).
Reducción del segundo cuadrante al primero
En el segundo cuadrante (90º – 180º) estamos tratando con ángulos suplementarios, lo cual quiere decir que entre los dos ángulos suman 180º. Por lo tanto, tenemos que hacer una reducción del segundo cuadrante al primero y esto lo hacemos con la fórmula 180 – α = β, siendo α el ángulo del primer cuadrante y β el ángulo original.
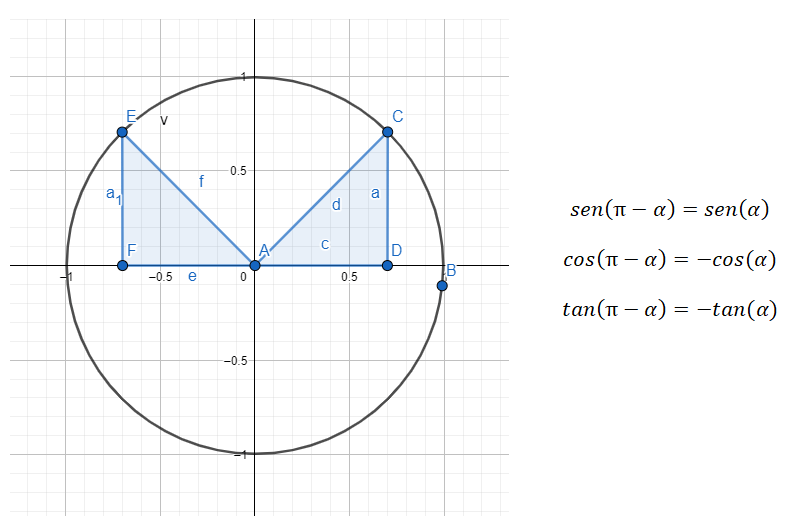
Por ejemplo, si nos dan el ángulo 135º (el cual pertenece al segundo cuadrante) tenemos que encontrar el ángulo del primer cuadrante que se relaciona con este primero. En este ejemplo, el ángulo (α) que buscamos es 45º, ya que 180 – 45 = 135. Por lo tanto, se cumplirá: sen (135) = sen (180 – 45) = sen (45), cos (135) = cos (180 – 45) = -cos (45) y tan (135) = tan (180 – 45) = -tan (45).
Reducción del tercer cuadrante al primero
En el tercer cuadrante (180º – 270º) estamos tratando con ángulos que difieren en 80º, lo cual quiere decir que los ángulos están a una distancia de 180º. Entonces, si queremos hacer una reducción del tercer cuadrante al primero, tenemos que usar la fórmula 180 + α = β, siendo α el ángulo del primer cuadrante y β el ángulo original.
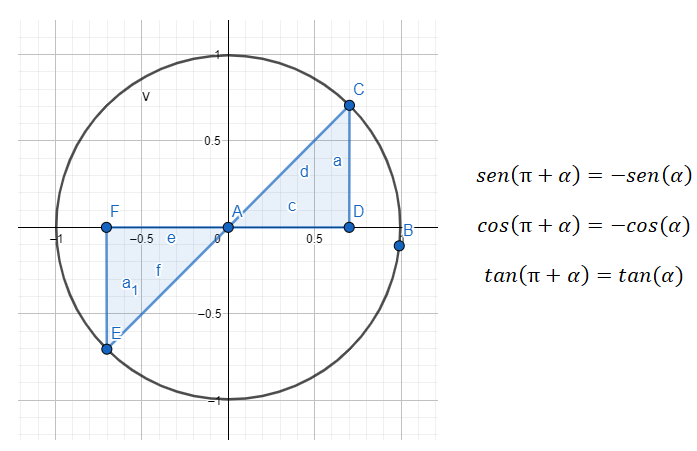
Por ejemplo, si nos dan el ángulo 225º (el cual pertenece al tercer cuadrante) tenemos que encontrar el ángulo del primer cuadrante que concuerda con este. En el caso del 225º, el ángulo (α) que estamos buscando es otra vez 45º, ya que 180 + 45 = 225. Por lo tanto, se cumplirá sen (225) = sen (180 + 45) = -sen (45), cos (225) = cos (180 + 45) = -cos (45) y tan (225) = tan (180 + 45) = tan (45).
Reducción del cuarto cuadrante al primero
En el cuarto cuadrante (270º – 360º) estamos tratando con ángulos opuestos, lo cual quiere decir que los ángulos son iguales numéricamente, pero tienen signo contrario, como por ejemplo el 30º y el -30º (equivalente a 330º, ya que 360º – 30º = 330º). Es importante tener en cuenta, que los ángulos opuestos se pueden escribir como un ángulo positivo y un ángulo negativo o como dos ángulos positivos, (en el ejemplo que acabamos de comentar hemos explicado la diferencia).
Entonces, si queremos hacer una reducción del cuarto cuadrante al primero tenemos que usar la fórmula 360 – α = β, siendo α el ángulo del primer cuadrante y β el ángulo original.
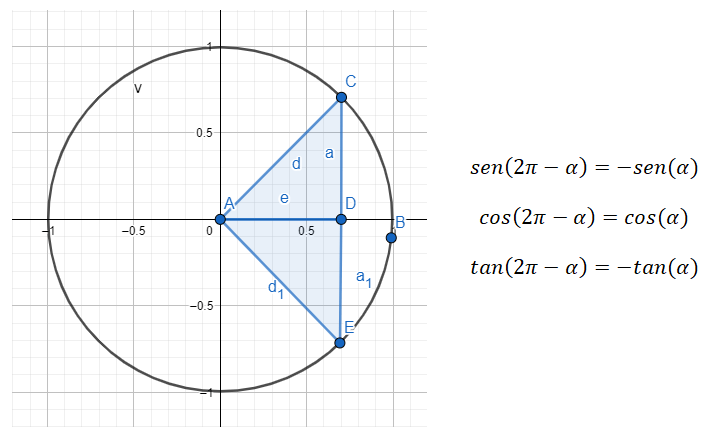
Por ejemplo, si nos dan el ángulo 315º (el cual pertenece al cuarto cuadrante) tenemos que encontrar el ángulo del primer cuadrante que se relaciona con este primero. En el caso del ángulo (α) que estamos buscando es otra vez 45º, ya que, 360 – 45 = 315. Por lo tanto, se cumplirá sen (315) = sen (360 – 45) = -sen (45), cos (315) = cos (360 – 45) = cos (45) y tan (315) = tan (360 – 45) = -tan (45). En conclusión, hemos visto los ángulos derivados de 45º de todos los cuadrantes.
Razones trigonométricas de los ángulos más importantes
Existen una serie de ángulos, llamados ángulos notables, los cuales son los más comunes en la trigonometría. Es muy recomendable saberse sus razones trigonométricas de memoria. Por lo tanto, a continuación hemos creado una tabla que contiene las razones trigonométricas de estos ángulos y de sus derivados (mismos ángulos, pero con una diferencia de 90, 180 o 270 grados):
| Ángulo (º) | Ángulo (rad) | Seno | Coseno | Tangente |
| 0º | 0 rad | 0 | 1 | 0 |
| 30º | 1/6 π rad | 1/2 | √3/2 | √3/3 |
| 45º | 1/4 π rad | √2/2 | √2/2 | 1 |
| 60º | 1/3 π rad | √3/2 | 1/2 | √3 |
| 90º | 1/2 π rad | 1 | 0 | ∞ |
| 120º | 5/8 π rad | √3/2 | -1/2 | -√3 |
| 135º | 3/4 π rad | √2/2 | -√2/2 | -1 |
| 150º | 5/8 π rad | 1/2 | -√3/2 | -√3/3 |
| 180º | π rad | 0 | -1 | 0 |
| 225º | 5/4 π rad | -√2/2 | -√2/2 | 1 |
| 270º | 3/2 π rad | -1 | 0 | ∞ |
| 315º | 7/4 π rad | -√2/2 | √2/2 | -1 |
Relación entre las razones trigonométricas
Existen bastantes maneras de relacionar las diferentes razones trigonométricas. A partir de estas relaciones, obtenemos una especie de igualdades entre las distintas funciones trigonométricas, las cuales se llaman identidades trigonométricas. Gracias a este tipo de identidades podemos calcular una razón en función de cualquier otra. Cabe destacar que hay muchos tipos de identidades trigonométricas diferentes, los cuales se clasifican según el tipo de relación que sustenta a la propia expresión.
Ejercicios resueltos de razones trigonométricas
A continuación, te planteamos una serie de ejercicios con los que podrás practicar toda la teoría explicada en este artículo. Recuerda que si en algún momento te bloqueas o te surge cualquier duda, puedes volver a leerte el artículo y seguramente, con una segunda lectura lo entenderás todo mucho mejor. Dicho esto, ya puedes empezar a practicar:
Ejercicio 1
Calcula las seis razones trigonométricas del ángulo 225º:
Empezaremos calculando el ángulo (α), el cual es igual a: 180 + α = 225º, por lo tanto, α = 45º.
sen (225) = sen (180 + 45) = -sen (45) = -√2/2
cos (225) = cos (180 + 45) = -cos (45) = -√2/2
tan (225) = tan (180 + 45) = tan (45) = 1
Ejercicio 2
Calcula las seis razones trigonométricas del ángulo 120º:
Empezaremos calculando el ángulo (α), el cual es igual a: 180 – α = 120º, por lo tanto, α = 60º.
sen (120) = sen (180 – 60) = sen (60) = √3/2
cos (120) = cos (180 – 60) = -cos (60) = -1/2
tan (120) = tan (180 – 60) = -tan (60) = -√3
Ejercicio 3
Calcula las seis razones trigonométricas del ángulo 510º:
Antes de empezar, tenemos que hacer la reducción de ángulos: 510 / 360 = 1 vuelta y un ángulo de 150 restante. Seguidamente, calculamos el ángulo (α), el cual es igual a: 180 – α = 150, por lo tanto, α = 30º.
sen (150) = sen (180 – 30) = sen (30) = 1/2
cos (150) = cos (180 – 30) = -cos (30) = -√3/2
tan (150) = tan (180 – 30) = -tan (30) = -√3/3