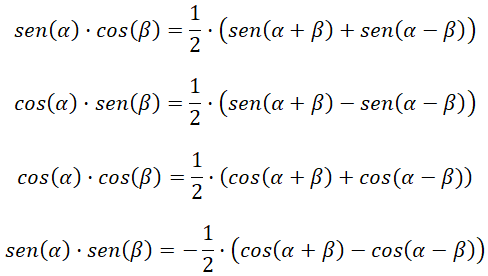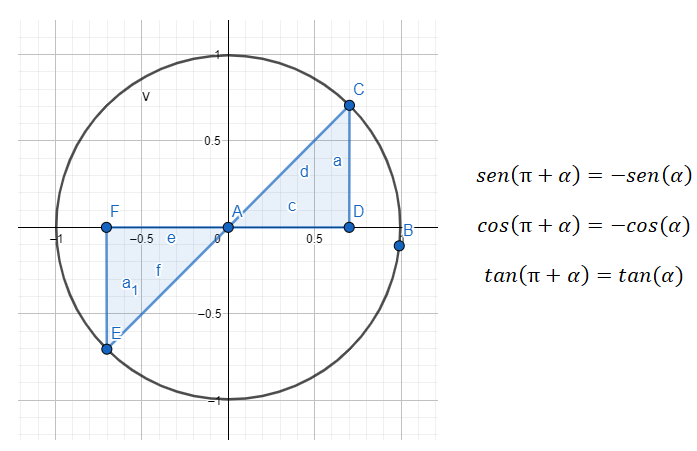Trigonometría

Las identidades trigonométricas son igualdades entre las diferentes funciones trigonométricas. Gracias a estas equivalencias trigonométricas, podemos deducir una determinada razón trigonométrica en función de cualquier otra. Por lo tanto, es necesario conocer las fórmulas de estas razones para poder comprender las fórmulas de las identidades trigonométricas. Si en tu caso no las conoces, te recomendamos que visites el último enlace.

Tabla de identidades trigonométricas

Identidades trigonométricas fundamentales

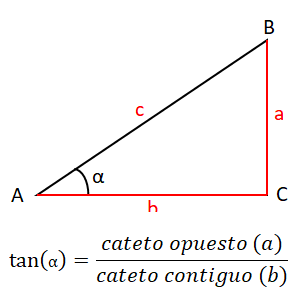
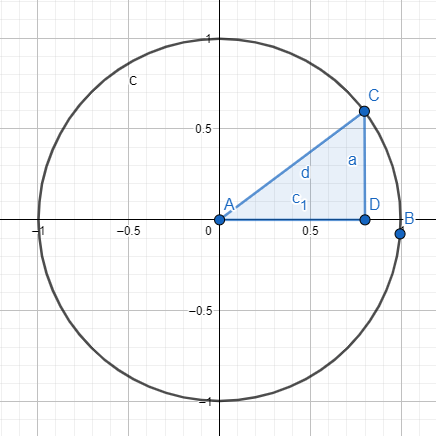
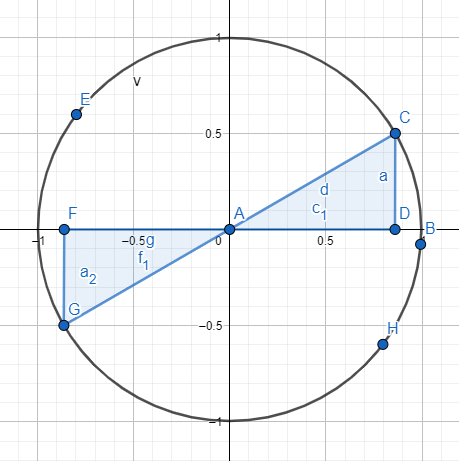
Existen una serie de identidades trigonométricas básicas que son consideradas las más importantes, esto se debe a que conforman la base teórica de las demás. Estas son las más comunes de encontrar y posiblemente, las más fáciles de recordar, ya que son bastante intuitivas. Recuerda que todas las fórmulas las basaremos en la siguiente imagen:

Identidad trigonométrica fundamental

La primera identidad de todas es la que se conoce como identidad trigonométrica fundamental, también conocida como relación entre seno y coseno. A continuación puedes encontrar su demostración matemática: sin² (α) + cos² (α) = 1.

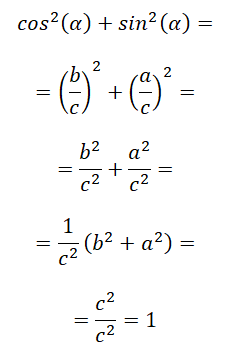
En el último paso, básicamente aplicamos el teorema de Pitágoras, porque c² = a² + b², entonces nos queda c² / c² lo cual es igual a 1. En conclusión, podemos afirmar que: sin² (α) + cos² (α) = 1.

Relación entre secante y tangente (secante al cuadrado)

En segunda instancia, tenemos una identidad trigonométrica que relaciona la secante con la tangente, su expresión es la siguiente: sec² (α) = 1 + tan² (α). En la siguiente imagen puedes ver algunas fórmulas de recordatorio que conforman esta identidad y después, el procedimiento para llegar a la fórmula final:

En este caso, estamos usando las fórmulas de las razones trigonométricas para hallar otras razones. En conclusión, podemos afirmar que: sec² (α) = 1 + tan² (α).

Relación entre cosecante y cotangente (cosecante al cuadrado)

A partir de la definición de cosecante y cotangente podemos encontrar una conexión en la fórmula de la tangente, es gracias a esta que podemos deducir otra identidad trigonométrica: cosec² (α) = 1 + cotg² (α).

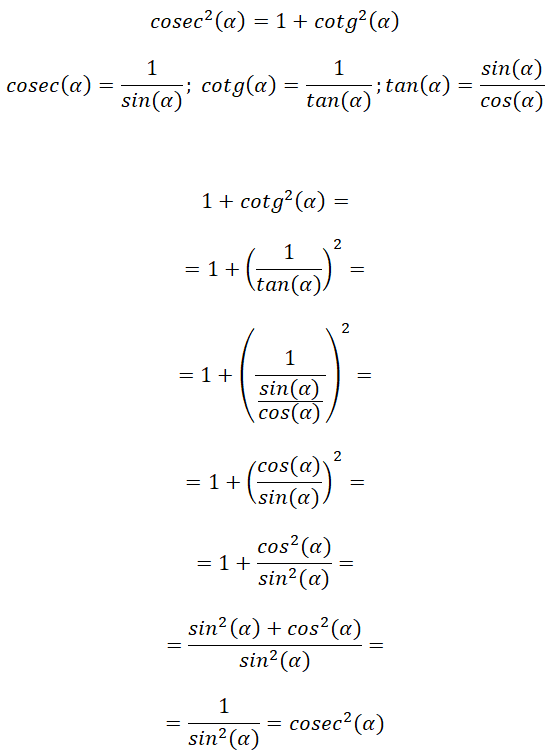
Con esta demostración podemos verificar que: cosec² (α) = 1 + cotg² (α). Además, podemos ver que esta relación guarda una cierta similitud con la anterior, lo cual se debe a la similitud entre tangente y cotangente.

Razones trigonométricas del ángulo suma y del ángulo resta

Las razones del ángulo suma o del ángulo resta son un tipo de identidades que se obtienen al calcular las razones trigonométricas de la suma o resta de dos ángulos. Por ejemplo, si queremos calcular el seno de 90 + 60, hay una serie de fórmulas que nos facilitan este cálculo. A continuación puedes encontrar una lista con todas las fórmulas de las identidades trigonométricas de este estilo:

Seno del ángulo suma: sen (α + β) = sen (α) · cos (β) + cos (α) · sen (β)

Seno del ángulo resta: sen (α – β) = sen (α) · cos (β) – cos (α) · sen (β)

Coseno del ángulo suma: cos (α + β) = cos (α) · cos (β) – sen (α) · sen (β)

Coseno del ángulo resta: cos (α – β) = cos (α) · cos (β) + sen (α) · sen (β)

Tangente del ángulo suma: tan (α + β) = (tan (α) + tan (β)) ÷ (1 – tan (α) · tan (β))

Tangente del ángulo resta: tan (α – β) = (tan (α) + tan (β)) ÷ (1 + tan (α) · tan (β))

Es evidente que calcular el seno de 150º es más fácil que usar las fórmulas que acabamos de explicar para calcular el seno de (90º + 60º). Por lo tanto, ¿Por qué son importantes estas fórmulas? Pues bien, la respuesta es que estas identidades nos permiten calcular las razones trigonométricas de ángulos complejos a partir de ángulos más simples. En consecuencia, si nos memorizamos las razones de los ángulos notables (los más relevantes), no nos hará falta utilizar la calculadora para calcular las razones de los ángulos más complejos como puede ser 150º.

Razones trigonométricas del ángulo doble

Cuando queremos calcular las razones trigonométricas de un ángulo doble (2α), podemos hacerlo por medio de una serie de identidades. Concretamente, lo podemos hacer a través de unas fórmulas muy similares a las que acabamos de comentar en el apartado previo. Ya que, si cambiamos β por α, en las anteriores expresiones, nos queda (α + α), lo cual es equivalente a (2α). Teniendo en mente esto, podemos deducir las siguientes identidades:

A continuación, puedes ver las demostraciones:

Seno del ángulo doble: sen (2α) = sen (α) · cos (α) + cos (α) · sen (α) = 2 · sen (α) · cos (α)

Coseno del ángulo doble: cos (α + α) = cos (α) · cos (α) – sen (α) · sen (α) = cos² (α) – sen² (α)

Tangente del ángulo doble: tan (2α) = 2 tan (α) ÷ (1 – tan² (α))

Razones trigonométricas del ángulo mitad

También, existen identidades que nos permiten calcular las razones trigonométricas del ángulo mitad (α/2):

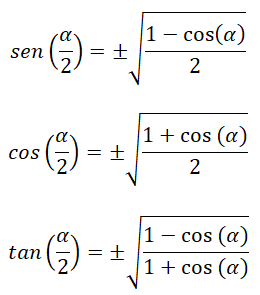
A partir de las fórmulas ya conocidas siguientes:

1 = sen² (β) + cos² (β)

cos (2β) = cos² (β) – sen² (β)

Si hacemos que β = α/2, entonces podemos demostrar estas identidades, restando ambas expresiones en el caso del seno, sumándolas en el caso del coseno y dividiendo las dos fórmulas obtenidas (la del seno y la del coseno) en el caso de la tangente. Solamente, falta aislar la razón que queramos calcular en las fórmulas que obtenemos a continuación:

Seno del ángulo mitad: 1 – cos (α) = 2 sen² (α/2); sen² (α/2) = (1 – cos (α)) ÷ 2

Coseno del ángulo mitad: 1 + cos (α) = 2 cos² (α/2); cos² (α/2) = (1 + cos (α)) ÷ 2

Razones trigonométricas del ángulo triple

En el caso de tener un ángulo triple (3α), también podemos usar unas identidades para calcular sus razones trigonométricas. Estas identidades provienen de las siguientes fórmulas ya explicadas: las identidades del ángulo doble, las identidades del ángulo suma y la identidad fundamental de la trigonometría.

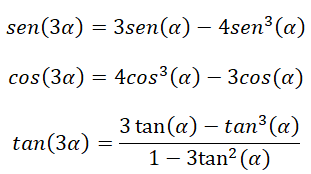
Para demostrar estas identidades, tenemos que recurrir a las fórmulas del ángulo suma:

Seno del ángulo suma: sen (3α) = sen (α + 2α) = sen (α) · cos (2α) + sen (2α) · cos (α)

Coseno del ángulo suma: cos (3α) = cos (α + 2α) = cos (α) · cos (2α) – sen (α) · sen (2α)

Entonces, si aplicamos las fórmulas del ángulo doble en las expresiones que acabamos de comentar y aplicamos la identidad fundamental de la trigonometría, podemos demostrar las identidades. Cabe mencionar que, el uso de la identidad trigonométrica fundamental nos permite convertir todas las razones de la expresión en una misma. Es por eso que la fórmula del seno del ángulo triple solo está compuesta por senos y la del coseno solamente contiene cosenos. A continuación, puedes ver el procedimiento completo:

Seno del ángulo triple: sen (3α) = sen (α + 2α) = sen (α) · cos (2α) + sen (2α) · cos (α) =

= sen (α) · (cos² (α) – sen² (α)) + 2 sen (α) · cos (α) · cos (α) =

= sen (α) · cos² (α) – sen³ (α) + 2 sen (α) · cos² (α) =

= sen (α) · (1 – sen² (α)) – sen³ (α) + 2 sen (α) · (1 – sen² (α)) =

= sen (α) – sen³ (α) – sen³ (α) + 2 sen (α) – 2 sen³ (α) =

= 3 sen (α) – 4 sen³ (α)

Coseno del ángulo triple: cos (3α) = cos (α + 2α) = cos (α) · cos (2α) – sen (α) · sen (2α) =

= cos (α) · (cos² (α) – sen² (α)) – sen (α) · 2 sen (α) · cos (α) =

= cos³ (α) – cos (α) · sen² (α) – 2 cos (α) · sen² (α) =

= cos³ (α) – 3 cos (α) · sen² (α) =

= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =

= cos³ (α) – 3 cos (α) + 3 cos³ (α) =

= 4 cos³ (α) – 3 cos (α)

Por último, la tangente del ángulo triple se puede calcular de dos maneras: la primera es dividiendo la fórmula del seno entre la del coseno y la segunda es sustituyendo la expresión de la tangente del ángulo doble, en la fórmula de la tangente del ángulo suma siguiente: tan (α + 2α) = (tan (α) + tan (2α)) ÷ (1 – tan (α) · tan (2α)).

Identidades trigonométricas según el tipo de ángulo

Es importante comentar una serie de fórmulas que son una especie de reglas para calcular razones trigonométricas de manera directa y rápida. De hecho, también se pueden considerar identidades trigonométricas, ya que, cumplen las mismas características que todas las expresiones que acabamos de comentar. Concretamente, estas fórmulas nos permiten determinar las razones trigonométricas de un ángulo a partir de la relación que mantiene con otro ángulo.

Ángulos complementarios

Los ángulos complementarios (α y β) son aquellos que tienen una suma igual a 90º, por lo tanto, cuando los sumamos obtenemos un ángulo recto. Para determinar que α es el ángulo complementario de β, tenemos que resolver una ecuación muy sencilla: α = 90 – β, si el resultado de esta equivalencia concuerda, entonces podemos afirmar que son complementarios. Gracias a estas identidades podemos deducir las razones trigonométricas de un ángulo a partir de las del otro.

Seno del ángulo complementario: sen (90º – α) = cos (α)

Coseno del ángulo complementario: cos (90º – α) = sen (α)

Tangente del ángulo complementario: tan (90º – α) = cotan (α)

Cosecante del ángulo complementario: cosec (90º – α) = sec (α)

Secante del ángulo complementario: sec (90º – α) = cosec (α)

Cotangente del ángulo complementario: cotan (90º – α) = tan (α)

Ángulos suplementarios

Los ángulos suplementarios (α y β) son aquellos que tienen una suma igual a 180º o π radianes, por lo tanto, podemos deducir la fórmula α + β = 180º. O dicho de otro modo, si el ángulo suplementario de α es β, entonces se tiene que cumplir la siguiente expresión β = 180 – α. A continuación, puedes ver el listado de identidades que podemos deducir sobre estos ángulos:

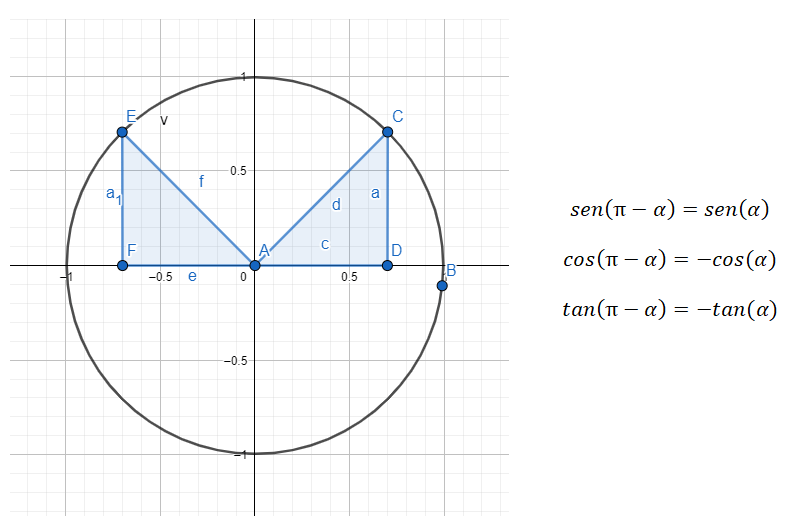
Seno del ángulo suplementario: sen (180º – α) = sen (α)

Coseno del ángulo suplementario: cos (180º – α) = -cos (α)

Tangente del ángulo suplementario: tan (180º – α) = -tan (α)

Cosecante del ángulo suplementario: cosec (180º – α) = cosec (α)

Secante del ángulo suplementario: sec (180º – α) = -sec (α)

Cotangente del ángulo suplementario: cotan (180º – α) = -cotan (α)

Ángulos conjugados

Los ángulos conjugados (α y β) son aquellos que tienen una suma igual a 360º o 2π radianes, es por ello que podemos deducir la fórmula α + β = 360º. Y a partir de esta primera fórmula, podemos expresar uno de los ángulos en función del otro de la siguiente manera: α = 360º – β o β = 360º – α. Ahora te mostraremos las igualdades de los ángulos conjugados:

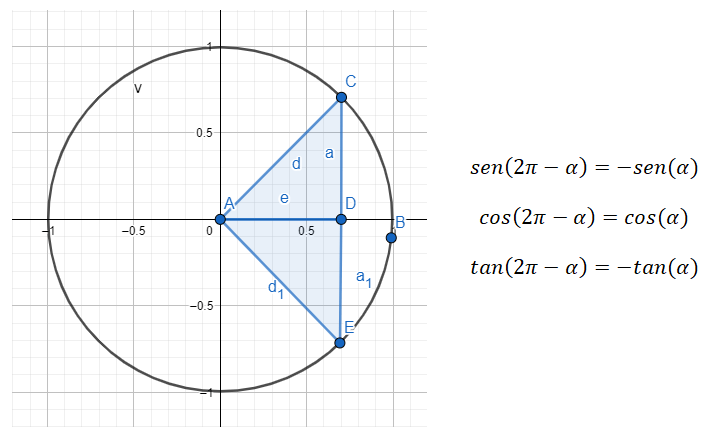
Seno del ángulo conjugado: sen (360º – α) = – sen (α)

Coseno del ángulo conjugado: cos (360º – α) = cos (α)

Tangente del ángulo conjugado: tan (360º – α) = – tan (α)

Cosecante del ángulo conjugado: cosec (360º – α) = – cosec (α)

Secante del ángulo conjugado: sec (360º – α) = sec (α)

Cotangente del ángulo conjugado: cotan (360º – α) = – cotan (α)

Ángulos opuestos

Los ángulos opuestos o ángulos negativos (α y β) son aquellos que tienen un mismo valor numérico, pero tienen diferente signo, un ejemplo de este tipo de ángulos son 30º y -30º. Algo que hay que tener en mente es que el signo negativo indica que el giro es en sentido horario, mientras que un ángulo positivo gira en sentido antihorario.

Seno del ángulo opuesto: sen (-α) = – sen (α)

Coseno del ángulo opuesto: cos (-α) = cos (α)

Tangente del ángulo opuesto: tan (-α) = – tan (α)

Cosecante del ángulo opuesto: cosec (-α) = – cosec (α)

Secante del ángulo opuesto: sec (-α) = sec (α)

Cotangente del ángulo opuesto: cotan (-α) = – cotan (α)

Ángulos que difieren en 90º o ángulos más/menos π/2

Los ángulos que difieren en 90º o ángulos más/menos π/2 (α y β) son aquellos que tienen una diferencia de 90º. Por lo tanto, se pueden expresar como β – α = 90º, siendo β 90º más grande que α. Estos ángulos también tienen una serie de fórmulas que relacionan las razones trigonométricas de ambos ángulos.

Seno del ángulo que difiere en 90º: sen (90º + α) = cos (α)

Coseno del ángulo que difiere en 90º: cos (90º + α) = -sen (α)

Tangente del ángulo que difiere en 90º: tan (90º + α) = – cotan (α)

Cosecante del ángulo que difiere en 90º: cosec (90º + α) = sec (α)

Secante del ángulo que difiere en 90º: sec (90º + α) = -cosec (α)

Cotangente del ángulo que difiere en 90º: cotan (90º + α) = -cotan (α)

Ángulos que difieren en 180º o ángulos más/menos π

Los ángulos más/menos π (α y β) equivalen a ángulos que difieren en 180º. Por lo tanto, se pueden expresar por medio de la fórmula siguiente: β – α = 180º, siendo β 180º más grande que α. A continuación, te mostramos las identidades trigonométricas que relacionan las razones trigonométricas de estos ángulos:

Seno del ángulo que difiere en 180º: sen (180º + α) = -sen (α)

Coseno del ángulo que difiere en 180º: cos (180º + α) = -cos (α)

Tangente del ángulo que difiere en 180º: tan (180º + α) = tan (α)

Cosecante del ángulo que difiere en 180º: cosec (180º + α) = -cosec (α)

Secante del ángulo que difiere en 180º: sec (180º + α) = -sec (α)

Cotangente del ángulo que difiere en 180º: cotan (180º + α) = cotan (α)

Transformaciones de razones trigonométricas

Por último, hay algunas identidades trigonométricas que nos permiten expresar una determinada razón trigonométrica por medio de otras operaciones. Entonces, si tenemos una suma de razones y queremos expresarlo en forma de producto, podemos recurrir a estas fórmulas. Aunque, por desgracia no hay una expresión para cada operación aritmética, solamente se puede pasar de suma o resta a producto y viceversa.

Transformar suma o resta en producto

Las siguientes cuatro fórmulas nos ayudan a calcular las sumas y las restas de las funciones trigonométricas:

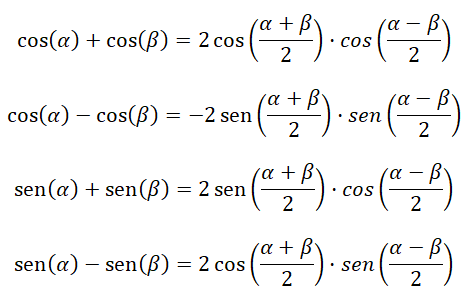
Transformar producto en suma o resta

Las siguientes cuatro fórmulas nos ayudan a calcular los productos de las funciones trigonométricas:

Las razones trigonométricas de un ángulo son las razones que se obtienen a partir de los tres lados de un triángulo rectángulo. Dicho de otro modo, son los valores que resultan de comparar por medio de cocientes (divisiones) sus tres lados. Aunque cabe destacar, que estas razones solamente existen en los triángulos rectángulos (triángulos que tienen un ángulo de 90º).

Razones trigonométricas en un triángulo rectángulo

Las seis razones trigonométricas más importantes son: seno, coseno, tangente, cosecante, secante y cotangente. A continuación, explicaremos en gran detalle cómo se define cada una de estas razones y hablaremos sobre la fórmula que las caracteriza. Para poder entender las siguientes explicaciones tomaremos en cuenta el siguiente triángulo rectángulo:

Seno

El seno de un ángulo (sen o sin) es igual al cociente del cateto opuesto (a) entre la hipotenusa (c), por lo tanto, la fórmula del seno es la siguiente: sen (α) = a / c. Es muy importante conocer esta definición de seno, ya que, esta es la base de toda la trigonometría, al igual que las otras razones que comentaremos en este apartado.

A través del teorema del seno, podemos calcular cualquier lado del triángulo, esto lo podemos hacer relacionando los cocientes de un determinado ángulo entre su lado correspondiente. Por ejemplo, si queremos calcular el lado a y tenemos los valores del lado b y de los ángulos A y B, podemos hacerlo usando la fórmula: a / sen (A) = b / sen (B). Resolviendo esta sencilla ecuación obtenemos el valor correspondiente a la variable que queremos calcular.

Coseno

El coseno de un ángulo (cos) es igual al cociente del cateto contiguo (b) entre la hipotenusa (c), por lo tanto, la fórmula del coseno queda así: cos (α) = b / c. En este caso, la fórmula está compuesta por los dos lados del triángulo que están en contacto con el ángulo que queremos estudiar, en este ejemplo, el ángulo A o α.

Con el coseno, también tenemos una manera de calcular los lados del triángulo, que es a partir del teorema del coseno. Este nos permite relacionar los lados con los ángulos y nos ofrece las siguientes tres expresiones:

a² = b² + c² – 2bc · cos (A)

b² = a² + c² – 2ac · cos (B)

c² = a² + b² – 2ab · cos (C)

Tangente

La tercera razón más importante, con la cual cerraremos el conjunto de razones originales, es la tangente (tan o tg). Esta se calcula haciendo la división entre el cateto opuesto (a) y el cateto contiguo (b), por lo tanto, la fórmula de la tangente nos queda así: tan (α) = a / b. A continuación, puedes verlo de manera gráfica:

La tangente también tiene un teorema propio, el cual se llama teorema de la tangente. Este nos permite relacionar las longitudes de dos lados de un triángulo con las tangentes de los ángulos. El enunciado es el siguiente: «el cociente de la suma de dos lados entre su resta es igual al cociente entre la tangente de la media de los dos ángulos opuestos a dichos lados y la tangente de la mitad de la diferencia de estos».

Razones trigonométricas derivadas

A partir de las tres razones trigonométricas que acabamos de comentar, podemos obtener otras razones trigonométricas derivadas. Estas se obtienen al hacer la razón inversa respecto al seno, coseno y tangente.

• Cosecante: es la razón inversa del seno y se calcula con las fórmulas: cosec (α) = c / a y cosec (α) = 1 / sen (α).
• Secante: es la razón inversa del coseno y se calcula con las fórmulas: sec (α) = c / b y sec (α) = 1 / cos (α).
• Cotangente: es la razón inversa de la tangente y se calcula con las fórmulas: cotg (α) = b / a y cotg (α) = 1 / tan (α).

Tabla de razones trigonométricas

A continuación, puedes ver una tabla que resume todas las razones explicadas hasta ahora. Con esta tabla podrás memorizar de manera eficiente todas las fórmulas, ya que, permite distinguir fácilmente las diferencias entre cada expresión matemática.

Razones trigonométricas en una circunferencia

Otra manera de estudiar la trigonometría es a través de la circunferencia goniométrica o círculo unitario, esta circunferencia tiene radio igual a 1 y su origen es el punto (0, 0). El dibujo consta de un círculo y de un triángulo rectángulo representado en el interior del círculo, concretamente, el ángulo que estudiaremos tiene que estar tocando el punto de origen.

Cuando tenemos esta imagen, sabemos que el radio es igual a la hipotenusa, el cual es igual a 1. Entonces, si queremos calcular el seno y el coseno, usaremos el valor del radio y el de los otros lados del triángulo. Para calcular el seno, haremos el siguiente cálculo: sen (A) = CD / AC = CD / radio = CD / 1 = CD, por lo tanto, el seno de A es a. Por otro lado, para calcular el coseno, haremos el cálculo: cos (A) = AD / AC = AD / radio = AD / 1 = AD, como resultado, el coseno de A es c1.

Es muy importante tener en cuenta dos cosas. La primera es que el uso de este círculo en el estudio de las razones trigonométricas, se debe a la necesidad de tratar con ángulos más grandes de los que se puede estudiar con el triángulo. Por ejemplo, el ángulo de 150º no se puede estudiar a través de un simple triángulo, dado que es demasiado grande. Y la segunda cosa a tener en cuenta es que tanto el seno como el coseno, nunca podrán adoptar valores mayores al 1 y menores al -1.

Signo de las razones trigonométricas

Como ya hemos dicho antes, para tratar con ángulos más grandes que los que nos permite tratar un triángulo, usamos la circunferencia goniométrica. Para hacerlo, representamos un triángulo en el interior del círculo exactamente en uno de los cuatro cuadrantes que dividen la circunferencia, en la siguiente imagen se pueden ver representados los cuatro cuadrantes.

Entonces, para poder distinguir entre un ángulo de 30 y uno de 210, que vienen a ser lo mismo en cuanto a la distribución dentro del triángulo, usaremos una distribución de signos según el cuadrante en el que se encuentre el triángulo. A continuación, puedes ver los signos correspondientes a cada cuadrante y un ejemplo dibujado.

Por ejemplo, los ángulos de 30º y de 210º comparten el mismo valor numérico, pero su seno y su coseno tienen signo contrario. Por lo tanto: sen (30) = 1/2 y cos (30) = √3/2, mientras que sen (210) = -1/2 y cos (210) = -√3/2. Para llegar a este resultado hemos representado ambos ángulos en la circunferencia (imagen de abajo) y hemos seguido las pautas de los signos.

Por último, comentar que es posible tener ángulos mayores a 360º, aunque no lo parezca porque la circunferencia es de tan solo 360º. Pero, si queremos resolver un ángulo de 750º, podemos hacer una reducción a un ángulo que esté entre 0º y 360º. Sencillamente, dividimos 750 entre 360 y el resto es el ángulo que nos queda, en el caso de 750º obtenemos un ángulo de 30º.

Tipos de ángulos según el cuadrante

Existen algunas relaciones entre diferentes ángulos, las cuales nos permiten calcular las razones trigonométricas de todos los ángulos pertenecientes a la circunferencia. Nos permiten obtener esas razones a partir de la reducción al primer cuadrante. Esto que quiere decir que hacemos una simplificación de un determinado ángulo al primer cuadrante y después aplicamos los signos correspondientes. A continuación puedes encontrar los diferentes procedimientos explicados (según el cuadrante):

Primer cuadrante

En este primer cuadrante (0º – 90º) solamente tenemos que resolver la razón trigonométrica con el ángulo que nos han dado. Y si nos fijamos en la imagen que hemos explicado anteriormente sobre los símbolos, tanto el seno como el coseno tienen un positivo delante (el resultado que obtengamos no se verá afectado por el signo).

Reducción del segundo cuadrante al primero

En el segundo cuadrante (90º – 180º) estamos tratando con ángulos suplementarios, lo cual quiere decir que entre los dos ángulos suman 180º. Por lo tanto, tenemos que hacer una reducción del segundo cuadrante al primero y esto lo hacemos con la fórmula 180 – α = β, siendo α el ángulo del primer cuadrante y β el ángulo original.

Por ejemplo, si nos dan el ángulo 135º (el cual pertenece al segundo cuadrante) tenemos que encontrar el ángulo del primer cuadrante que se relaciona con este primero. En este ejemplo, el ángulo (α) que buscamos es 45º, ya que 180 – 45 = 135. Por lo tanto, se cumplirá: sen (135) = sen (180 – 45) = sen (45), cos (135) = cos (180 – 45) = -cos (45) y tan (135) = tan (180 – 45) = -tan (45).

Reducción del tercer cuadrante al primero

En el tercer cuadrante (180º – 270º) estamos tratando con ángulos que difieren en 80º, lo cual quiere decir que los ángulos están a una distancia de 180º. Entonces, si queremos hacer una reducción del tercer cuadrante al primero, tenemos que usar la fórmula 180 + α = β, siendo α el ángulo del primer cuadrante y β el ángulo original.

Por ejemplo, si nos dan el ángulo 225º (el cual pertenece al tercer cuadrante) tenemos que encontrar el ángulo del primer cuadrante que concuerda con este. En el caso del 225º, el ángulo (α) que estamos buscando es otra vez 45º, ya que 180 + 45 = 225. Por lo tanto, se cumplirá sen (225) = sen (180 + 45) = -sen (45), cos (225) = cos (180 + 45) = -cos (45) y tan (225) = tan (180 + 45) = tan (45).

Reducción del cuarto cuadrante al primero

En el cuarto cuadrante (270º – 360º) estamos tratando con ángulos opuestos, lo cual quiere decir que los ángulos son iguales numéricamente, pero tienen signo contrario, como por ejemplo el 30º y el -30º (equivalente a 330º, ya que 360º – 30º = 330º). Es importante tener en cuenta, que los ángulos opuestos se pueden escribir como un ángulo positivo y un ángulo negativo o como dos ángulos positivos, (en el ejemplo que acabamos de comentar hemos explicado la diferencia).

Entonces, si queremos hacer una reducción del cuarto cuadrante al primero tenemos que usar la fórmula 360 – α = β, siendo α el ángulo del primer cuadrante y β el ángulo original.

Por ejemplo, si nos dan el ángulo 315º (el cual pertenece al cuarto cuadrante) tenemos que encontrar el ángulo del primer cuadrante que se relaciona con este primero. En el caso del ángulo (α) que estamos buscando es otra vez 45º, ya que, 360 – 45 = 315. Por lo tanto, se cumplirá sen (315) = sen (360 – 45) = -sen (45), cos (315) = cos (360 – 45) = cos (45) y tan (315) = tan (360 – 45) = -tan (45). En conclusión, hemos visto los ángulos derivados de 45º de todos los cuadrantes.

Razones trigonométricas de los ángulos más importantes

Existen una serie de ángulos, llamados ángulos notables, los cuales son los más comunes en la trigonometría. Es muy recomendable saberse sus razones trigonométricas de memoria. Por lo tanto, a continuación hemos creado una tabla que contiene las razones trigonométricas de estos ángulos y de sus derivados (mismos ángulos, pero con una diferencia de 90, 180 o 270 grados):

Relación entre las razones trigonométricas

Existen bastantes maneras de relacionar las diferentes razones trigonométricas. A partir de estas relaciones, obtenemos una especie de igualdades entre las distintas funciones trigonométricas, las cuales se llaman identidades trigonométricas. Gracias a este tipo de identidades podemos calcular una razón en función de cualquier otra. Cabe destacar que hay muchos tipos de identidades trigonométricas diferentes, los cuales se clasifican según el tipo de relación que sustenta a la propia expresión.

Ejercicios resueltos de razones trigonométricas

A continuación, te planteamos una serie de ejercicios con los que podrás practicar toda la teoría explicada en este artículo. Recuerda que si en algún momento te bloqueas o te surge cualquier duda, puedes volver a leerte el artículo y seguramente, con una segunda lectura lo entenderás todo mucho mejor. Dicho esto, ya puedes empezar a practicar:

Ejercicio 1

Calcula las seis razones trigonométricas del ángulo 225º:

Empezaremos calculando el ángulo (α), el cual es igual a: 180 + α = 225º, por lo tanto, α = 45º.

sen (225) = sen (180 + 45) = -sen (45) = -√2/2

cos (225) = cos (180 + 45) = -cos (45) = -√2/2

tan (225) = tan (180 + 45) = tan (45) = 1

Ejercicio 2

Calcula las seis razones trigonométricas del ángulo 120º:

Empezaremos calculando el ángulo (α), el cual es igual a: 180 – α = 120º, por lo tanto, α = 60º.

sen (120) = sen (180 – 60) = sen (60) = √3/2

cos (120) = cos (180 – 60) = -cos (60) = -1/2

tan (120) = tan (180 – 60) = -tan (60) = -√3

Ejercicio 3

Calcula las seis razones trigonométricas del ángulo 510º:

Antes de empezar, tenemos que hacer la reducción de ángulos: 510 / 360 = 1 vuelta y un ángulo de 150 restante. Seguidamente, calculamos el ángulo (α), el cual es igual a: 180 – α = 150, por lo tanto, α = 30º.

sen (150) = sen (180 – 30) = sen (30) = 1/2

cos (150) = cos (180 – 30) = -cos (30) = -√3/2

tan (150) = tan (180 – 30) = -tan (30) = -√3/3