¿Qué es el método de los mínimos cuadrados?

El método de los mínimos cuadrados es una herramienta matemática para encontrar la mejor línea recta que se ajuste a un conjunto de puntos. Te lo explicamos de manera sencilla:

Imagina que tienes un conjunto de puntos en un gráfico dispersos por aquí y por allá. Quieres encontrar una línea recta que “se ajuste” lo mejor posible a esos puntos, de manera que minimice la distancia entre la línea y los puntos. Esa es la idea detrás del método de los mínimos cuadrados.

El método utiliza una fórmula para calcular la ecuación de la línea que minimiza la suma de los cuadrados de las diferencias entre los puntos y la línea. Es decir, busca la línea que tenga la menor “desviación” respecto a los puntos.

En palabras simples, el método de los mínimos cuadrados es útil para el análisis de datos arrojados en una investigación, con el objetivo de expresar cómo se comportan de forma lineal, reduciendo los errores de la información sustraída.

¿Quién creó el método de los mínimos cuadrados?

El método de los mínimos cuadrados, una herramienta fundamental en estadística y análisis de datos, se atribuye al matemático alemán Carl Friedrich Gauss, quien lo propuso en 1794. Sin embargo, Gauss no lo publicó hasta 1809.

Curiosamente, el matemático francés Andrien-Marie Legendre publicó una versión similar en 1805, desarrollándolo de forma independiente.

Ambos matemáticos contribuyeron a la creación de este método que ha sido ampliamente utilizado en diversas disciplinas para ajustar modelos a datos observados y hacer predicciones precisas.

Fórmula del método de mínimos cuadrados

Sin duda, para entender lo que implica este método, es esencial explicar su fórmula y proceso de realización. Aquí tienes una explicación detallada de la fórmula del método de los mínimos cuadrados:

Definir el problema

Supongamos que tienes un conjunto de datos con dos variables, una variable independiente (x) y una variable dependiente (y), y quieres ajustar una línea recta a esos datos.

El objetivo es encontrar los valores de los coeficientes de la ecuación de la línea (intercepto y pendiente) que minimicen la suma de los cuadrados de las diferencias entre los valores reales de y, y los valores predichos por la línea ajustada.

Calcular la ecuación de la línea

La ecuación de una línea recta tiene la forma y = mx + b, donde m es la pendiente y b es el intercepto. La fórmula del método de los mínimos cuadrados para calcular los valores de m y b es la siguiente:

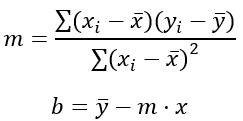
Donde:

Σ representa la suma de los valores.

x_i y y_i son los valores de las variables x e y respectivamente para cada punto de datos.

x̄ y ȳ son las medias de los valores de x e y respectivamente.

(x_i – x̄) y (y_i – ȳ) son las diferencias entre los valores de x e y y sus medias respectivas.

(x_i – x̄)² es el cuadrado de la diferencia entre el valor de x y su media.

Interpretar los resultados

Una vez que has calculado los valores de m y b usando la fórmula, puedes utilizarlos para obtener la ecuación de la línea recta ajustada. Por ejemplo, si obtuviste m = 2 y b = 3, entonces la ecuación de la línea ajustada sería y = 2x + 3. Esto te permite hacer predicciones o estimaciones de los valores de y para diferentes valores de x en función de la línea ajustada.

¿En qué casos se usa el método de mínimos cuadrados?

Seguramente, te preguntarás ¿Cuándo se emplea este método? ¡Es muy útil en varias situaciones! Por ejemplo, cuando quieres analizar datos experimentales o de investigación para encontrar una relación o tendencia.

Supongamos que estás investigando cómo el precio de una casa está relacionado con su tamaño en metros cuadrados. Podrías utilizar el método de mínimos cuadrados para encontrar la línea recta que mejor se ajuste a los datos y te dé una idea clara de esa relación.

También se usa en la economía para modelar y predecir variables como la demanda de productos o el comportamiento de los precios. Además, en la ingeniería, el método de mínimos cuadrados se aplica para ajustar modelos matemáticos a datos de pruebas o simulaciones.

El método de mínimos cuadrados es una herramienta poderosa y versátil que se emplea en muchas áreas de estudio y trabajo para analizar datos y encontrar relaciones importantes.

Aplicaciones del método de mínimos cuadrados en otros teoremas

Además de su utilización en sí mismo, el método de mínimos cuadrados es bastante útil en otros teoremas. Veamos un poco más sobre el tema, a continuación.

Teorema de Regresión

Es ampliamente usado en el teorema de regresión para encontrar la mejor línea que se ajuste a un conjunto de datos. Por ejemplo, puedes emplearlo para analizar la relación entre la altura de una planta y la cantidad de luz que recibe para determinar cómo la planta crecerá en diferentes condiciones de luz.

Teorema de Interpolación

En este caso, el método de mínimos cuadrados también se aplica en el teorema de interpolación para encontrar la función polinómica que mejor se ajuste a un conjunto de puntos. Por ejemplo, puedes utilizarlo para aproximar la trayectoria de un objeto en movimiento basado en datos de posición y tiempo.

Teorema de Ajuste de Curvas

Sirve en el teorema de ajuste de curvas para encontrar una curva que se ajuste a un conjunto de datos. Esto es útil en aplicaciones como el modelado de datos climáticos para predecir el cambio climático o en la predicción de la trayectoria de un proyectil.

Teorema de Análisis de Fourier

En el teorema de análisis de Fourier, el método de mínimos cuadrados se usa para aproximar una función periódica a partir de una serie de datos discretos. Esto se aplica en la señalización de datos y en la compresión de imágenes y sonido.

Teorema de Regresión No Lineal

Finalmente, el método de mínimos cuadrados también se aplica en el teorema de regresión no lineal para encontrar la mejor curva que se ajuste a un conjunto de datos que no sigue una relación lineal. Por ejemplo, puedes emplearlo para analizar cómo la concentración de un producto químico afecta la tasa de reacción.

Ejemplo del método de mínimos cuadrados

Para comprender mejor la forma en que puedes aplicar el método de mínimos cuadrados, observemos un ejemplo, a continuación.

Supongamos que tienes los siguientes datos de altura (en centímetros) de una planta en diferentes semanas:

Semana	Altura en centímetros
1	10
2	12
3	14
4	16
5	18
6	20

Quieres encontrar la mejor línea recta que se ajuste a estos datos para hacer una predicción de la altura futura de la planta.

Paso 1: Graficar los datos

Lo primero que debes hacer es graficar los datos en un gráfico de dispersión. El eje x representará las semanas y el eje y representará la altura en centímetros. Aquí está el gráfico:

Paso 2: Aplicar el método de mínimos cuadrados

El método de mínimos cuadrados busca encontrar una línea recta que minimice la suma de los cuadrados de las diferencias entre los datos reales y los valores predichos por la línea. En este caso, la línea se representa por la ecuación de una recta: y = mx + b, donde “y” es la altura, “x” son las semanas, “m” es la pendiente de la línea y “b” es el intercepto en el eje y.

Para encontrar los valores de “m” y “b” que minimicen la suma de los cuadrados de las diferencias, se utilizan las siguientes fórmulas:

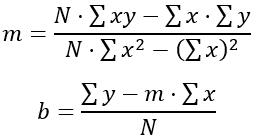
Donde N es el número de datos (en este caso, 6), Σxy es la suma del producto de las semanas por las alturas, Σx es la suma de las semanas, Σy es la suma de las alturas, y Σx² es la suma de los cuadrados de las semanas.

Aplicando estas fórmulas a los datos de altura, se obtiene:

Σxy = 1·10 + 2·12 + 3·14 + 4·16 + 5·18 + 6·20 = 630

Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21

Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90

Σx² = 1² + 2² + 3² + 4² + 5² + 6² = 91

Sustituyendo estos valores en las fórmulas de “m” y “b”:

m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21²) ≈ 2,07

b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24

Por lo tanto, la ecuación de la línea recta que se ajusta a los datos de altura es: y.