Los cuadrados mágicos son un juego matemático para pensar, el cual entrena nuestra capacidad de cálculo de una manera divertida y emocionante. Es por eso que es uno de los mejores recursos para enseñar matemáticas a los estudiantes jóvenes.
Contenido
¿Qué es un cuadro mágico y cómo se resuelve?
Un cuadrado mágico es una especie de tabla o matriz que está compuesta por diferentes casillas, en las cuales se escriben números enteros. Pero, no se pueden poner de cualquier manera, hay que seguir una serie de normas:
- Todas las sumas mágicas (sumas de todos los valores de cualquier línea horizontal, vertical o diagonal) tienen que dar siempre el valor equivalente a la constante mágica (es un valor único).
- No se puede repetir ningún número dos veces.
- Solamente puedes usar números consecutivos (por ejemplo, del 1 al 9) o números que siguen una determinada serie, por ejemplo: números impares, múltiplos de 5, entre otras.
También, es importante destacar que podemos hacer diferentes clasificaciones de cuadrados según la estructura de estos. La primera es según el grado del cuadrado, el cual equivale al número de casillas que hay en una línea o en una columna. Y la segunda es según el tipo de grado de la tabla (números pares o números impares). A partir de estas distinciones, podemos organizar todos los cuadrados en diferentes categorías, aunque esto lo detallaremos más adelante.

¿Cómo resolver cuadrados mágicos?
Para resolver este juego matemático podemos usar dos métodos distintos: usar la geometría o calcular la constante mágica. Ambos procedimientos son igual de válidos, aunque uno te permite llegar de una manera más rápida al resultado, mientras que el otro requiere de más tiempo y razonamiento. A continuación, te explicaremos ambos métodos, así podrás elegir el que más te guste y podrás adaptarte mejor a cada situación.
¿Cuál es la fórmula de los cuadros mágicos?
El primer método consiste en calcular la constante mágica, para lo cual tenemos que usar la siguiente fórmula: n(n2+1)/2, siendo n el grado del cuadrado. Y una vez tenemos este valor, solamente nos queda ir probando las diferentes combinaciones de números, que nos permiten igualar las sumas mágicas de todo el cuadrado a la constante. Dicho de otra manera, tenemos que formar combinaciones de números que sumen el valor de la constante, de tal forma que nos cuadre toda la tabla.
¿Cómo resolver cuadrados mágicos usando la geometría?
En segunda instancia, podemos resolver los cuadrados mágicos por medio de la geometría. Aunque cabe destacar que este método es muy sencillo y no te hace ejercitar tu capacidad de cálculo, ya que es puramente metódico. Dicho esto, te explicaremos el procedimiento tanto para resolver cuadrados de orden par como cuadrados de orden impar.
¿Cómo resolver cuadrados mágicos con números impares?
Para resolver este primer caso, tenemos que añadir casillas a la tabla inicial de tal manera que nos quede una especie de rombo. Seguidamente, tenemos que escribir todos los números consecutivos empezando por la primera cifra de la serie (en nuestro caso el 1) y seguiremos las diagonales del rombo. Finalmente, tenemos que «doblar» la figura, por lo tanto, los valores de las casillas externas pasan al lado contrario. Entonces, las celdas externas del eje vertical se cruzan y después pasa lo mismo con las celdas del eje horizontal, a continuación puedes ver un ejemplo:

¿Cómo resolver cuadrados mágicos de orden par?
Para resolver un cuadrado mágico de orden par (cuadrados mágicos que tienen un número par de filas y columnas) podemos recurrir a un método algo distinto al anterior, pero que también se basa en la geometría. Empezaremos escribiendo la primera cifra de la serie (en nuestro caso el 1) en la esquina superior izquierda. Después, nos desplazaremos por las dos diagonales principales e iremos escribiendo los valores correspondientes a la posición de cada casilla.
Una vez tengamos escritas las dos diagonales principales tendremos que situarnos en la primera casilla en blanco empezando desde la esquina inferior derecha (la casilla 15 en nuestro caso). Ahí escribiremos el segundo valor de la serie e iremos apuntando los valores restantes por orden (de más pequeños a más grandes), completando las celdas de derecha a izquierda y de abajo a arriba. Para que quede más claro, puedes orientarte con la imagen que te mostramos a continuación:

¿Cómo construir cuadrados mágicos?
Para construir cuadrados mágicos nosotros mismos podemos seguir varios procedimientos, de entre los cuales destacaremos dos. Cabe mencionar que cada uno se usará para crear cuadrados de diferentes tipos, por lo tanto, deberás elegir el método cuidadosamente según el cuadrado que quieras generar:
Método siamés
Este primer método es bastante sencillo, y concretamente nos sirve para construir cuadrados mágicos impares de cualquier tamaño. El procedimiento a seguir es muy simple, básicamente escribiremos el primer número de la serie en la casilla central de la primera fila. A partir de ahí, iremos subiendo por orden en la progresión aritmética que hayamos escogido, escribiendo el siguiente número hacia arriba y hacia la derecha. Aunque, si esa posición queda fuera de la casilla dibujada, entonces tendremos que movernos a la última fila o última columna. Y si nos encontramos con una casilla llena, tendremos que bajar un cuadrado respecto a la casilla del último número que hayamos puesto y después seguiremos igual.
A continuación puedes ver un ejemplo de 3×3:
Método de Strachey para cuadrados mágicos
Para generar cuadrados mágicos de orden 4k + 2 pares, usaremos este otro método, el cual está basado en el anterior (el método siamés) y también es muy sencillo. A continuación, puedes ver los pasos a seguir y un ejemplo resuelto de un cuadrado mágico 6×6:
- Dividir en cuadrantes más pequeños: lo primero que tenemos que hacer es subdividir la tabla en cuadrados más pequeños, por ejemplo si tenemos una tabla 6×6, tendremos que hacer cuatro cuadrantes iguales de 3×3 casillas.
- Usar el método siamés: después asignaremos un rango de números a cada cuadrante pequeño, por ejemplo si empezamos la secuencia por el 1, los rangos quedarían: 1-9 (primero), 10-18 (cuarto), 19-27 (segundo) y 28-36 (tercero).

Método LUX de Conway para cuadrados mágicos
Usaremos este último sistema cuando queramos generar cuadrados mágicos de orden 4n + 2, siendo n un número natural. Entonces, el procedimiento que seguiremos para crear cuadrados de este estilo es el siguiente:
- Creación de la tabla o matriz: empezaremos creando una matriz de grado 2n + 1, siendo n un número natural. Con esto, podremos diseñar la tabla y tendremos en mente el grado de esta, para después empezar con el diseño.
- Posicionamiento de las letras: una vez tengamos la tabla construida, tendremos que escribir de arriba a abajo: n + 1 filas de L, 1 fila de U y n – 1 filas de X. Y después, tendremos que intercambiar la U del medio con la L de arriba.
- Intercambio de las letras por los valores numéricos: ahora tendremos que reemplazar las letras por grupos de cuatro números consecutivos. Dependiendo de la letra daremos un orden u otro a los números. Explicado a continuación:
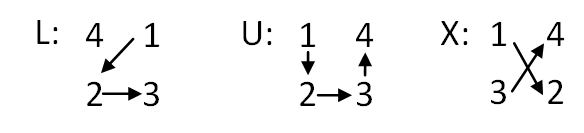
Empezaremos construyendo una matriz de 5×5, por lo tanto, n = 2, ya que: 2n + 1 = 2 · 2 + 1 = 5. Esto quiere decir que la matriz acabará siendo de un tamaño 10×10, porque como ya hemos dicho, cada casilla que contenga una letra equivale a un grupo de cuatro números, es decir, una matriz de 2×2. A continuación, puedes ver el ejemplo terminado, en el cual hemos ido sustituyendo cada letra por un grupo de cuatro números en el orden que se ve en la imagen:

Ejercicios de cuadrados mágicos
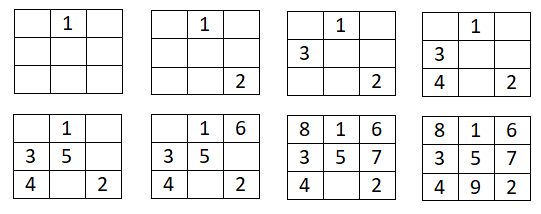
A continuación, te planteamos algunos cuadrados mágicos que están incompletos y tendrás que llenarlos tú, gracias a los conceptos que hemos explicado en este artículo. Recuerda que puedes usar cualquiera de los métodos enseñados. También, deberás tener en cuenta que quizás el 1 no sea el primer número de la serie, aunque, en el enunciado lo pondrá. Y cuando hayas completado alguno de los ejercicios, podrás visualizar la solución situada debajo del enunciado.
Cuadrado mágico 3×3
Construye un cuadrado mágico 3×3 solamente con números impares:

Cuadrado mágico 4×4
Completa el siguiente cuadrado mágico 4×4:

Cuadrado mágico 5×5
Completa el siguiente cuadrado mágico 5×5:

Cuadrado mágico 6×6
Completa el siguiente cuadrado mágico 6×6:
