Funciones polinómicas

En este artículo encontrarás una explicación muy detallada sobre las funciones polinómicas, la cual está complementada con ejemplos. Además, podrás ver cómo se utilizan las funciones polinomiales en la vida cotidiana gracias a los ejercicios que te plantearemos al final.

¿Qué es una función polinómica?

Las funciones polinómicas o funciones polinomiales son unas funciones las cuales vienen dadas por una expresión algebraica equivalente a un polinomio. Esto quiere decir que la expresión deberá seguir la estructura de un polinomio: f(x) = a₀ + a₁x + a₂x² + a₃x³ + … + a_nxⁿ, según la estructural del cual se determinará el tipo de función polinómica que trataremos. Otra característica muy relevante de estas funciones es que todos sus exponentes de las incógnitas son positivos y enteros.

Partes de una función polinómica

Podemos destacar tres elementos importantes respecto a estas funciones:

• Coeficientes del polinomio: son los números que acompañan a las incógnitas, por ejemplo el 3 del siguiente término es un coeficiente: 3x². Cabe destacar que hay tantos coeficientes como términos tiene el polinomio.
• Exponentes o índices del polinomio: son las potencias de las incógnitas, por ejemplo el 2 del siguiente término es un exponente: 3x². Y como ya hemos explicado, en el caso de una función polinómica siempre serán positivos y enteros.
• Grado del polinomio: este valor es equivalente al exponente de mayor grado de entre todos los términos que componen el polinomio. En el caso del polinomio f(x) = 3x² – 4x + 2, el grado es igual a dos.

¿Cómo saber si una función es polinomial o no?

Para identificar una función polinómica deberemos fijarnos en si cumple las características que acabamos de comentar. Empezaremos comprobando si la expresión que define a la función tiene una estructura polinómica: f(x) = a₀ + a₁x + a₂x² + a₃x³ + … + a_nxⁿ. Y después, verificaremos que los índices sean positivos y enteros, con estos sencillos pasos podremos determinar si una función es polinomial o no.

Tipos de funciones polinómicas con ejemplos

A continuación, te mostraremos los diferentes tipos de funciones polinómicas que existen, los cuales están clasificados según el grado del polinomio. Además, encontrarás una representación gráfica de ejemplo para cada tipo. Gracias a estos ejemplos de funciones polinomiales podrás ver mejor las diferencias entre las distintas categorías.

Funciones constantes

Las funciones constantes equivalen a un polinomio de grado 0, esto quiere decir que el coeficiente de x es 0. Es por eso, que las funciones de este tipo no dependen del valor de la variable independiente x. Por lo tanto, su representación gráfica es una recta horizontal, la cual es infinita. A continuación puedes encontrar representado el ejemplo f(x) = 3:

Funciones polinómicas de primer grado

En segundo lugar, encontramos las funciones polinómicas de primer grado, las cuales vienen dadas por un polinomio de grado 1 con la siguiente estructura: f(x) = mx + n. Esta expresión está compuesta por un número llamado pendiente (m) el cual multiplica a la variable x y por una constante (n) que se suma a ese producto. Entonces, según los valores de m y n, podemos identificar tres tipos diferentes de funciones:

• Funciones afines: este subtipo se caracteriza por tener un valor de n diferente a 0, o dicho de otro modo, el valor de la ordenada es diferente a 0. Por lo tanto, este tipo de funciones no pasa por el punto (0, 0), también conocido como el origen. También comentar que si la m < 0, la función será decreciente, mientras que si la m > 0, la función será creciente.
• Funciones lineales: la única distinción que tienen estas funciones respecto a las funciones afines es que la n = 0, por lo tanto, no tienen ordenada. Como resultado, la expresión de las funciones lineales es equivalente a f(x) = mx. Este tipo es bastante fácil de representar, ya que, siempre pasa por el punto (0, 0) y a partir del pendiente ya obtienes la gráfica.
• Funciones identidad: este último tipo es un subgrupo de las funciones lineales, el cual tiene n = 0 y m = 1. Esto quiere decir que la expresión se queda f(x) = x, con lo cual la representación gráfica es una diagonal que forma un ángulo de 45º con cualquiera de los ejes. Este tipo de funciones también pasa por el punto de origen (0, 0).

A continuación, puedes encontrar un ejemplo de función polinómica de primer grado, concretamente de una función afín f(x) = 3x + 2:

Funciones cuadráticas

Las funciones cuadráticas o funciones de segundo grado se expresan por medio de polinomios de segundo grado, los cuales siguen la estructura: f(x) = ax² + bx + c, siendo a diferente de 0. En este caso, la representación gráfica es bastante más compleja, puesto que ya no es una línea recta, sino una parábola vertical. A continuación, puedes encontrar la representación de la función cuadrática f(x) = 2x² + 4x – 1:

Funciones cúbicas

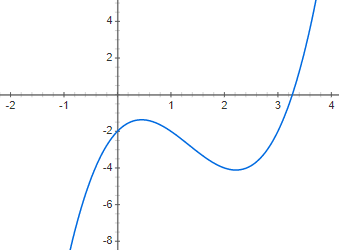
Las funciones cúbicas o funciones de tercer grado vienen dadas por un polinomio de grado tres: f(x) = ax³ + bx² + cx + d, siendo a diferente a 0. La representación de una función de este estilo es aún más compleja que la de segundo grado, ya que, puede tener varias formas diferentes. Aunque la forma básica, o al menos la más común, es la que te mostraremos en el ejemplo siguiente, f(x) = 2x³ – 4x² + 2x – 2:

Propiedades de las funciones polinómicas

Las funciones polinómicas tienen una serie de propiedades o características que las distinguen del resto de funciones, a continuación te las detallaremos de la manera más clara posible. De esta manera, cuando veas alguna función de este tipo te será muy fácil identificarlas:

• El dominio de una función polinómica es igual a todos los números reales: Dom f = R o Dom f = (-∞, ∞), por lo tanto, son continuas en todo el conjunto de reales.
• Su punto de corte del eje Y es equivalente (0, a₀), siendo a₀ el término independiente.
• Corta por el eje X un número de veces igual o inferior al grado del polinomio.
• Las funciones polinómicas no tienen asíntotas.
• Si el exponente de todos los términos es impar, entonces la representación de la gráfica es simétrica respecto al origen de coordenada, mientras que si el exponente de todos los términos es par, esta es simétrica respecto al eje OY.
• El número de puntos de inflexión que tiene una función de este estilo es igual o menor a n – 2, siendo n el grado.
• El número de máximos y mínimos relativos que tiene una función de este estilo es igual o menor a n – 1, siendo n el grado.

¿Cómo se analiza una función polinómica?

Para analizar una función polinómica deberemos seguir el mismo procedimiento que usaríamos para analizar cualquier otra función. En la siguiente lista hemos resumido los diferentes elementos que hay que estudiar o tratar:

• Dominio y recorrido
• Puntos de corte con los ejes horizontal y vertical
• Monotonía (crecimiento y decrecimiento, máximos y mínimos)
• Curvatura (en las funciones de grado mayor a uno)

Evidentemente, podemos llevar el análisis a otro nivel y estudiar muchos más elementos, aunque con estos debería bastar. Ya que, conociendo estos elementos tendrás una idea clara de cómo es la función y podrás representarla gráficamente.

Ejercicios de funciones polinómicas

A continuación, te planteamos una serie de ejercicios para que practiques la representación de funciones, concretamente de funciones polinómicas. De esta manera, consolidarás todos los conceptos explicados en este artículo:

Ejercicio 1

Representa gráficamente la siguiente función polinómica de primer grado f(x) = x + 2 y di de qué tipo es:

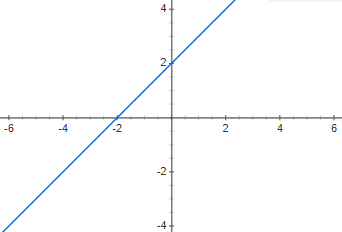
Es una función polinómica de primer grado afín, puesto que tiene una n diferente a 0 y una m diferente a 0.

Ejercicio 2

Representa gráficamente la siguiente función polinómica de segundo grado f(x) = x² + x – 2:

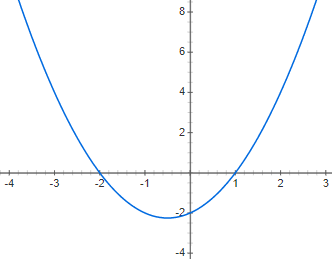
Ejercicio 3

Representa gráficamente la siguiente función polinómica de tercer grado f(x) = x² + x – 2: