El número de Euler (también conocido como la constante de Euler) es un número matemático importante y esencial en diversas áreas de las matemáticas, incluyendo la teoría de números, la topología, la teoría de grupos y la teoría de funciones. Se representa con la letra griega «e» y su valor aproximado es 2,71828.
El número e surge de la fórmula de la función exponencial y es un número fundamental en la teoría de los números complejos.
También es un número natural que aparece en la resolución de muchos problemas matemáticos, incluyendo el cálculo de probabilidades y la modelización de procesos de crecimiento y decay.
Contenido
¿Cuál es el origen del número Euler?
El número de Euler fue nombrado en honor al matemático suizo Leonhard Euler (1707-1783), quien fue uno de los más grandes matemáticos de todos los tiempos y es considerado el padre de la matemática moderna.
Euler hizo valiosas contribuciones en muchas áreas de las matemáticas, incluyendo la teoría de números, la geometría, el cálculo, la física y la astronomía.
Fue él quien primero definió y utilizó el número e (llamado el número de Euler) en su trabajo en cálculo y teoría de logaritmos. La fórmula de Euler para números complejos también es una de sus contribuciones más notables a la matemática.
¿Cómo se obtiene este valor?
A decir verdad, hay diversos métodos para calcular el número de Euler. Sin embargo, cabe mencionar que ningún método arroja un resultado exacto. Por lo tanto, su numeración es continúa e infinita, pero no se repite.
De hecho, en la actualidad, se conocen hasta más de 1 billón de números que forman la cifra del número e. La serie infinita que define el número de Euler es:
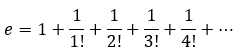
Donde «!» es factorial, que se define como el producto de todos los números naturales hasta ese número. Por ejemplo:
5! = 5 · 4 · 3 · 2 · 1 = 120
Podemos ver gráficamente esta serie como la suma de una serie de rectángulos con altura 1 y anchura decreciente, donde la anchura de cada rectángulo es 1/n!, donde n es el número de factoriales.
Si aumentamos el número de rectángulos en la suma, la aproximación al área bajo la curva de la función exponencial se acerca cada vez más al número de Euler.
En resumen, el número de Euler es un número que surge de la suma de una serie infinita y es fundamental en muchas áreas de las matemáticas. Aunque es un número irracional, su valor aproximado es 2,71828.
Es importante tener presente que el mismo Euler implementó este método para realizar el cálculo de e con 18 decimales.
Otra forma de calcularlo:
Podemos calcular el valor aproximado del número de Euler en una recta utilizando una serie de términos finitos. Por ejemplo, si tomamos la primera serie infinita que se definió anteriormente:
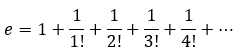
Podemos calcular el valor aproximado sumando los primeros términos de la serie. Por ejemplo, si sumamos los primeros 6 términos:

Podemos representar esta serie en una recta para ver cómo se acerca al valor aproximado de 2,71828.
Gráficamente, la recta que representa el número de Euler se puede dibujar con una serie de rectángulos con altura 1 y anchura decreciente, donde la anchura de cada rectángulo es 1/n!, donde n es el número de factoriales.
Si aumentamos el número de rectángulos en la suma, la aproximación al área bajo la curva de la función exponencial se acerca cada vez más al número de Euler.
Ecuaciones exponenciales con el número Euler
Las ecuaciones exponenciales con el número de Euler pueden ser usadas para modelar una amplia variedad de fenómenos en ciencias como la física, la biología, la economía, entre otros. Algunos ejemplos incluyen:
Crecimiento y decadencia exponencial
Este modelo describe la tasa en la que una población crece o decrece, o la tasa de descomposición de una sustancia tóxica.
Por ejemplo, si una población está creciendo a una tasa del 5% por año, su tamaño puede ser descrito por la fórmula:
P(t) = P0 · e0,05t, donde P0 es el tamaño inicial de la población.
Modelos de desintegración radioactiva
Este modelo describe la tasa en la que los átomos radiactivos se desintegran con el tiempo.
La fórmula es la siguiente:
N(t) = N0 · e-λt
Donde N0 es el número inicial de átomos, λ es una constante que depende del material radioactivo y t es el tiempo.
Estos son solo algunos ejemplos de cómo se pueden emplear las ecuaciones exponenciales con el número de Euler en la práctica. Hay muchos otros campos en los que las ecuaciones exponenciales son útiles y relevantes.
¿Cuáles son las aplicaciones del número Euler?
El número de Euler tiene una amplia gama de aplicaciones en diferentes campos de la matemática y las ciencias. Algunos de los campos en los que se utiliza el número e son los siguientes:
- Cálculo y análisis matemático: se utiliza en el estudio de las funciones exponenciales y logarítmicas, y en la solución de ecuaciones diferenciales.
- Teoría de números: se utiliza en el estudio de la distribución de los números primos y en la solución de problemas relacionados con la teoría de números.
- Probabilidad y estadística: se emplea en la solución de problemas relacionados con la distribución de probabilidad y en la estimación de valores esperados.
- Criptografía: se usa en el estudio de los algoritmos de cifrado y descifrado.
- Física: se utiliza en la solución de problemas relacionados con la termodinámica, la mecánica cuántica y la física estadística.
- Química: se emplea en la solución de problemas relacionados con la termodinámica química y la cinética química.
Fórmula de Euler para números complejos
La fórmula de Euler para números complejos establece una relación entre las funciones trigonométricas y exponenciales. La fórmula se escribe como:

Donde “e” es la base de los logaritmos naturales, “i” es la unidad imaginaria, ”x” es un número real y “cos” y “sen” son las funciones trigonométricas coseno y seno, respectivamente.
Esta fórmula es muy útil en muchas áreas de la matemática, incluyendo la teoría de números, la teoría de funciones y la teoría de la complejidad, y tiene una gran variedad de aplicaciones en la ingeniería, la física y la economía.
Un ejemplo práctico de su uso es en la representación de señales y sistemas en el análisis de Fourier, en el cual las señales periódicas se representan como una suma de señales sinusoidales complejas.
La fórmula de Euler se utiliza para describir la forma en que estas señales complejas se relacionan con las funciones trigonométricas reales que describen las señales sinusoidales individuales.
El número Euler y el interés compuesto
El interés compuesto es un concepto financiero que describe el proceso por el cual una cantidad de dinero, llamada capital, genera intereses sobre el interés acumulado a lo largo del tiempo.
En otras palabras, los intereses generados por una inversión no solo provienen del capital inicial, sino también de los intereses generados en períodos previos.
El número de Euler y el interés compuesto están relacionados porque la fórmula para calcular el interés compuesto utiliza el número de Euler. La fórmula para el interés compuesto es:
A = P · ert
Donde A es el monto final, P es el principal, r es la tasa de interés, t es el tiempo y e es el número de Euler. De esta manera, el número de Euler es un factor importante en la formulación matemática para el cálculo del interés compuesto.
Un ejemplo de cálculo de interés compuesto con números concretos sería el siguiente:
Supongamos que tenemos una inversión de 1000 € a una tasa de interés del 5% anual durante 2 años. La fórmula para calcular el interés compuesto sería:
A = P · ert = 1000 · e0,05 · 2 = 1000 · 1,1025 = 1102,5 €.
Esto significa que después de 2 años, nuestro capital inicial de 1000 € habrá crecido a 1102,5 € debido al interés compuesto generado.
Ejemplos de ejercicios matemáticos con el número Euler
Aquí están dos ejemplos de ejercicios resueltos de matemáticas que involucran el número de Euler:
1. Encuentra el valor de «eix» donde x es un número real:
La identidad de Euler nos dice que eix = cos(x) + i · sen(x). Por lo tanto, si conocemos el valor de x, podemos calcular el valor de eix utilizando las funciones trigonométricas.
2. Calcula e^(x2) para un valor dado de x:
Podemos utilizar la serie de Taylor para calcular el valor de e^(x2). La serie de Taylor de ex es una expansión infinita que permite calcular aproximaciones sucesivas del valor de ex, dependiendo del término que se use.
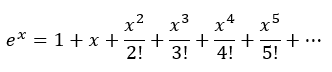
Si sustituimos x2 en lugar de x en esta serie, obtenemos la serie de Taylor para e^(x2).