¿Alguna vez te has preguntado cómo los números racionales se diferencian de otros números? En este artículo, exploraremos en profundidad los números racionales, incluyendo sus características únicas y cómo se clasifican. ¡Prepárate para entender mejor el concepto!
Contenido
¿Qué son los números racionales?
Los números racionales (ℚ) son una subclase de los números reales que incluye a todos los números que se pueden expresar como una fracción. Esto significa que los números racionales son aquellos que se pueden escribir como un cociente de dos enteros, a/b, donde b ≠ 0.
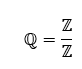
Los números racionales también se pueden expresar como decimales periódicos o finitos, ya que están formados por una serie de dígitos repetidos. Algunos ejemplos de números racionales son 1/2, 3/4, 10/3, 2/3 y π (pi).
Subconjuntos de los racionales
Los números racionales se pueden dividir en dos subconjuntos:
- Los números enteros, que incluyen al 0, a todos los números naturales y a todos los números negativos.
- Los números decimales o números fraccionarios, que son todos aquellos que expresan valores formados por: una parte entera y una parte decimal, esta última permite expresar valores menores que la unidad.

Otra subcategoría del conjunto de los reales son los números irracionales, los cuales son algo más complejos.
Ejemplos de números racionales
Los números racionales son aquellos que se pueden expresar como una fracción, es decir, como un cociente de dos números enteros. Algunos ejemplos de números racionales son:
-2/3
-4/5
-1/2
-7/9
Todas las fracciones que representan a un número entero, también son racionales. Por ejemplo:
-1/1
-2/2
-3/3
Propiedades de los números racionales
La característica principal de los números racionales es que siempre tienen un denominador distinto de cero.
La segunda propiedad de este conjunto, es que cada número racional puede representarse con infinitas fracciones equivalentes. Por ejemplo, el número racional 3,5, que es igual a 7/2, también puede escribirse como 14/4, 28/8…, e infinitas fracciones más.
Los números racionales también cumplen con la propiedad distributiva. Esto quiere decir que, al multiplicar o dividir una fracción por otra, el resultado no se verá afectado:
(a/b)·(c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
Representación de los números racionales
Los números racionales se pueden representar de varias maneras, pero la forma más común es mediante una fracción. La fracción consiste en dos números: el numerador y el denominador.
El numerador indica cuántas partes del todo se están considerando, mientras que el denominador indica cuántas partes iguales hay en el todo. Por ejemplo, si un pastel se divide en ocho porciones iguales y se come tres de esas porciones, entonces la fracción que representa la cantidad de pastel que se ha comido sería 3/8.
Otra forma de representar los números racionales es mediante decimales. Los decimales son una forma abreviada de escribir una fracción en la que el denominador es un número de 10, 100, 1000, etc. Por ejemplo, si se tiene 1/4 de un pastel, esto se puede expresar como 0,25 (que significa «0 enteros y 25/100»).
Aunque, si queremos representarlos de forma gráfica, también podemos escribirlos en la recta numérica, en la cual se puede apreciar muy bien el orden de los números. A continuación, te mostramos un ejemplo de esta recta:
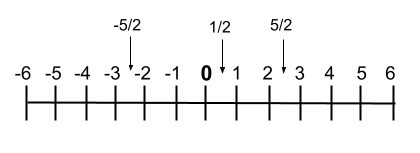
Operaciones racionales
Las operaciones fundamentales de los números racionales son las mismas que las de los números enteros: la suma, la resta, la multiplicación y la división. Si quieres aprender a resolver este tipo de operaciones, te recomendamos que te leas nuestro artículo sobre operaciones con fracciones.
Aunque, si estás operando con números racionales en base decimal, debes seguir el procedimiento de resolución de operaciones que empleas cuando tratas con valores decimales.
Conclusión sobre el conjunto de los números racionales
Después de esta exhaustiva explicación, podemos concluir que el conjunto de los números racionales es uno de los más importantes en las matemáticas. Contiene a todos los números que se pueden representar como una fracción, lo cual nos permite expresar cantidades de manera muy precisa.