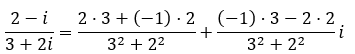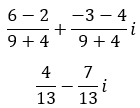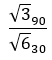En este artículo, vamos a explicar cómo resolver operaciones con números complejos. Detallaremos los métodos que pueden usarse para cada operación. De este modo, sabrás cómo actuar en cada situación.
Contenido
Suma y resta de números complejos
Vamos a empezar explicando cómo sumar y restar números complejos en forma binómica. Sencillamente, debemos operar como cuando lo hacemos con expresiones algebraicas. Debemos sumar o restar las partes reales y las partes imaginarias por separado. A continuación, te explicamos cómo resolver ambas operaciones.
Para sumar en forma binómica debemos seguir esta fórmula que es muy intuitiva (tal como hemos dicho antes, esta fórmula parte de la premisa de que debemos separar las partes reales de las imaginarias):
(a + bi) + (c + di) = (a + c) + (b + d)i
Trata de resolver la siguiente suma: (2 + 5i) + (-3 + 2i)
Para restar en forma binómica debemos hacer lo mismo, pero con el signo negativo:
(a + bi) – (c + di) = (a – c) + (b – d)i
Ahora, trata de resolver la siguiente resta: (3 – 4i) – (5 + 2i)
Multiplicación de números complejos
Ahora pasamos a la multiplicación de números complejos. Aunque, cabe destacar que se nos pueden plantear dos casos. El primero es una multiplicación de números complejos en forma binómica. Y el segundo es una multiplicación de números complejos en forma polar. Vamos a ver un ejemplo resuelto de ambos casos.
Para multiplicar en forma binómica, podemos usar la siguiente fórmula:
(a + bi) · (c + di) = (ac – bd) + (ad + bc)i
Aunque, en realidad, sencillamente debemos aplicar el sentido común, pues se resuelve igual que una multiplicación algebraica.
Intenta resolver la multiplicación en forma binómica: (2 + 4i) · (3 – 2i)
En cambio, para resolver una multiplicación en forma polar, debemos multiplicar los módulos y sumar los argumentos (o ángulos). La siguiente expresión describe muy bien el procedimiento a seguir:
|z|a · |w|b = (|z| · |w|)a+b
Ahora, prueba de resolver esta multiplicación en forma polar: √245 · 260
División de números complejos
La cuarta operación aritmética con números complejos es la división, la cual es relativamente sencilla. Igual que con la multiplicación, se nos pueden plantear dos casos. El primero es una división de números complejos en forma binómica y el segundo es una división de números complejos en forma polar. Vamos a ver ambas:
Para resolver una división en forma binómica, podemos aplicar la siguiente fórmula:

Aunque, al igual que pasa con las multiplicaciones, también pueden resolverse como si fueran divisiones algebraicas.
Prueba de resolver la siguiente división en forma binómica: (2 – i) ÷ (3 + 2i)
Y para resolver divisiones con números complejos en forma polar, solamente hay que aplicar la siguiente fórmula:
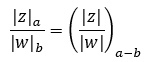
A ver si puedes resolver la siguiente división en forma polar: √390 ÷ √630