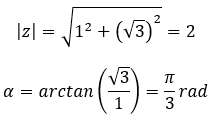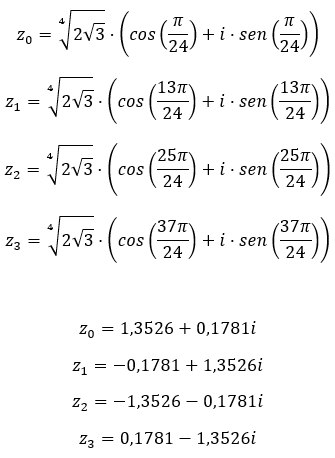Calcular raíces de números complejos es algo bastante sencillo. Pues, una vez entiendes el procedimiento, este es bastante repetitivo. A continuación, vamos a explicarlo y te plantearemos algún ejemplo, para que aprendas a aplicarlo en ejercicios reales.
Contenido
Raíces enésimas de números complejos
El concepto de raíz enésima equivale a decir raíz de orden n, por lo tanto, el mismo método sirve para calcular la raíz cuadrada y la raíz quinta de un número complejo. Eso sí, el número de soluciones cambiará en función de ese orden.
Por ejemplo, si calculamos la raíz cuarta de un complejo, obtenemos 4 soluciones diferentes. Y si lo expresamos en el plano complejo, podemos ver que se forma un polígono regular de 4 lados, centrado en el origen del plano. Esta es una propiedad muy interesante, que veremos en detalle más adelante (en el apartado de los ejemplos).
Ahora que ya hemos clarificado este concepto, vamos a ver cómo se calcula la raíz de un número complejo en forma polar (usar esta notación es la más cómoda para resolver una raíz.). Sencillamente, hay que calcular la raíz del módulo y expresar el argumento en función de n. Dicho de otra manera, la raíz del siguiente número complejo (z):

Equivale a calcular:
- Módulo: La raíz enésima del módulo inicial.
- Argumento: Sumarle al argumento 2πk en radianes o 360k en grados, y dividirlo todo entre n.
Matemáticamente, para calcular el módulo y el argumento usamos las siguientes dos fórmulas:

Donde, k = 0, 1, 2, …, n-1.
Y, por lo tanto, el resultado lo expresamos tal que así:

Para que quede claro, las n soluciones que obtendremos de resolver esta raíz estarán formadas por el mismo módulo y n argumentos diferentes.
Ejemplos del cálculo de raíces enésimas de complejos
Ahora vamos a ver un par de ejemplos sobre el cálculo de raíces enésimas de números complejos. Te recomendamos que trates de resolverlos por tu cuenta y cuando acabes, mires la corrección. Recuerda que el método está explicado justo arriba.
Calcula la raíz tercera del número complejo: 1 + i√3.

Calcula la raíz cuarta del número complejo: 3+i√3.