La distancia es una magnitud física que mide cuánto hay entre dos puntos, por lo tanto, nos permite establecer la proximidad o lejanía que hay entre dos ubicaciones. Aunque a primera vista pueda resultar difícil hacer este tipo de cálculos, existe una fórmula muy sencilla para calcular la distancia entre dos puntos, y hoy te enseñaremos cómo hacerlo.
Contenido
Calculadora de la distancia entre dos puntos
En esta sección, te ofrecemos una calculadora de distancias entre dos puntos, la cual es muy intuitiva y fácil de usar. Solamente, tienes que introducir las coordenadas de los dos puntos y la calculadora te dará el resultado numérico. Ten en cuenta, que las unidades que uses en las coordenadas de entrada han de ser las mismas con las que quieras el resultado.
¿Cómo calcular la distancia entre dos puntos usando la fórmula de Pitágoras?
¿Cómo podemos calcular la distancia entre dos puntos en un plano? Hay varias formas de hacerlo, aunque son muy similares. La primera es calculando el módulo del vector que viene dado por los puntos (A y B), lo cual se calcula haciendo la raíz cuadrada de la diferencia de cada componente: x2 – x1 e y2 – y1, (en la siguiente imagen encontrarás la fórmula).
Otra manera de hacerlo es calculando la distancia euclidiana, que se deduce a partir del teorema de Pitágoras. La distancia euclidiana es la medida más natural de la separación entre dos puntos y se define como la raíz cuadrada de la suma de las diferencias al cuadrado entre cada una de las coordenadas. Que es básicamente la misma definición que la anterior.
Este último método proviene del teorema pitagórico, el cual dice que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (la línea que une los dos vértices opuestos del triángulo) es igual a la suma del cuadrado de las longitudes de los otros dos lados del triángulo.
Por lo tanto, si unimos los dos puntos (A y B) con una línea (la recta r), y descomponemos esa recta en rx y ry, obtenemos un triángulo rectángulo que podemos usar para determinar la longitud de la recta r. En ambos casos, obtenemos la misma expresión matemática, puesto que viene a ser el mismo cálculo.
A continuación, te mostramos una imagen donde quedan representadas todas las variables y elementos que hemos comentado hasta ahora.
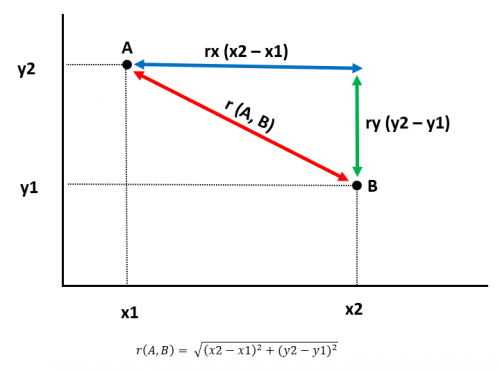
Distancia euclidiana en 3 dimensiones
Y si queremos calcular la distancia que hay entre dos puntos en un espacio tridimensional, solamente tenemos que adaptar un poquito la fórmula. En vez de hacer el cálculo con solo dos componentes, añadiremos una tercera (componente z), la cual nos permitirá «ampliar» el cálculo y la fórmula final quedará tal que así:

Ejemplos del cálculo de la distancia entre dos coordenadas
A continuación, te mostramos un ejemplo del cálculo de la distancia entre dos puntos. Partiendo de los puntos A(1, 3, -4) y B(2, -1, 5), en metros. Solamente, tenemos que aplicar la fórmula de la distancia euclidiana que te acabamos de mostrar en la imagen de arriba. Mira la resolución numérica para acabar de entender el procedimiento:

Aplicaciones prácticas de la fórmula para calcular la distancia entre dos puntos
Hay muchas aplicaciones prácticas de esta fórmula para calcular la distancia entre dos puntos. Por ejemplo, podemos usarla para determinar la distancia entre dos ciudades o para calcular el tiempo que tarda un objeto en recorrer una determinada distancia.
También podemos usarla para encontrar la ruta más corta entre dos puntos o para determinar el punto medio de una longitud. Es por eso, que saber calcular la distancia entre dos puntos es muy útil para nuestra vida diaria.
Gracias por leer este artículo, si quieres aportar alguna conclusión que hayas sacado de todo esto o simplemente dejar tu opinión, puedes dejarlo aquí abajo.
