El número Pi es una constante matemática que representa la relación entre la circunferencia de un círculo y su diámetro. Es un número irracional. Es decir, no es una fracción exacta. Por ello, no se puede representar como un número decimal finito. El valor de Pi es aproximadamente 3,14159 y se representa con la letra griega π.
Pi es un número importante en matemáticas. Por lo tanto, tiene muchas aplicaciones en diversas áreas. Por ejemplo, se utiliza en la geometría para calcular el área. Asimismo, el perímetro de círculos y otras figuras circulares. Por su parte, en la trigonometría para calcular ángulos y longitudes de arcos. Finalmente, en la ingeniería y la física para calcular magnitudes como el volumen y la capacitancia.
El día de Pi se celebra el 14 de marzo de cada año, ya que la fecha se aproxima al valor de Pi (3,14). Esta fecha se celebra para conmemorar el papel de Pi en las matemáticas y para promover el interés por esta fundamental constante.
Contenido
¿Quién descubrió el número Pi?
El número Pi ha sido conocido desde la antigüedad, y fue el matemático griego Arquímedes (287-212 a.C.) quien lo describió por primera vez de manera precisa. De hecho, lo usó para calcular el área y el volumen de figuras geométricas.
En el siglo XVIII, el matemático suizo Johann Lambert demostró que Pi es un número irracional. Más adelante, en el siglo XIX, el matemático alemán Ferdinand von Lindemann expuso que Pi es un número trascendental. Es decir, que no se puede expresar como una solución exacta de una ecuación polinómica con coeficientes racionales.
A lo largo de la historia, diferentes matemáticos han contribuido a la comprensión del número Pi y han desarrollado técnicas para calcularlo con mayor precisión. En la actualidad, Pi sigue siendo una de las constantes matemáticas más importantes y conocidas en el mundo y sigue siendo un tema de estudio en las matemáticas.
¿Por qué el número Pi es infinito?
El valor de Pi es aproximadamente 3,14159, pero en realidad, es un número que continúa indefinidamente después del punto decimal. Esto significa que Pi es un número infinito y no se puede representar completamente como un número decimal.
Aunque el valor de Pi es infinito, en la práctica se pueden calcular valores aproximados de Pi con mucha precisión. En la actualidad, se han calculado millones de dígitos de Pi y se ha demostrado que no tiene patrones regulares en sus dígitos decimales. Aunque, esto se ha hecho a través de superordenadores, puesto que nosotros no podemos calcular tantos dígitos.
¿Qué métodos existen para calcular el valor aproximado del número Pi?
Existen diversos métodos prácticos para calcular el valor de Pi. A continuación, te explicamos paso a paso los tres métodos más utilizados por los matemáticos.
1. Método de Arquímedes
El matemático griego Arquímedes empleó un método geométrico para calcular un valor aproximado de Pi. Para usar este método, sigue los siguientes pasos:
1. Dibuja un círculo y traza una línea que pase por el centro del círculo y corte a este por dos puntos opuestos, como se muestra a continuación:

2. Mide la longitud de la línea que corta al círculo y llámala “D”. Esta medida es el diámetro del círculo.
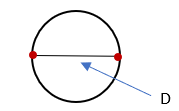
3. Mide la longitud de la línea que forma el círculo y llámala “C”. Esta medida es la circunferencia del círculo.

4. Divide la circunferencia del círculo (C) por el diámetro del círculo (D). El resultado es un valor aproximado de Pi.
Por ejemplo: si el diámetro del círculo es 6 y la circunferencia es 18, entonces el valor aproximado de Pi es 18 ÷ 6 = 3. Evidentemente, este ejemplo es muy básico, pero si lo haces con valores de una circunferencia real, verás que el método funciona correctamente.
De hecho, te recomendamos que pruebes de hacerlo: coge las medidas de una taza o algo que tenga una forma circular y, comprueba si te funciona.
2. Método de Montecarlo
El método de Montecarlo es un método probabilístico que se usa para calcular valores aproximados de Pi. Para ello, se generan aleatoriamente una gran cantidad de puntos en un plano y se cuenta cuántos puntos caben dentro de un círculo inscrito en un cuadrado. El proceso se aplica de la siguiente forma:
1. Dibuja un círculo dentro de un cuadrado de lado 1, como se muestra a continuación:

2. Genera aleatoriamente una gran cantidad de puntos en el cuadrado.

3. Cuenta cuántos puntos caben dentro del círculo. Llama a esta cantidad “n”.

4. Cuenta cuántos puntos en total se generaron. Llama a esta cantidad “m”.
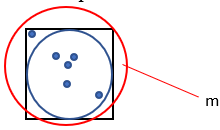
5. Calcula el valor aproximado de Pi utilizando la siguiente fórmula: Pi = (4 · n) ÷ m.
Por ejemplo, si se generaron 380 puntos y 300 caben dentro del círculo, entonces el valor aproximado de Pi es (4 · 300) ÷ 380 = 3,16. Este valor se parece bastante a las dos primeras cifras decimales de Pi, pero, de igual manera que con el anterior método, si utilizas medidas reales, obtendrás un valor aún más exacto.
3. Método de iteración
El método de iteración es un método matemático que se utiliza para calcular valores aproximados de Pi. Este método usa una fórmula que involucra el valor de Pi y se aplica iterativamente para mejorar la precisión del cálculo. A continuación, los pasos para utilizar este método:
- Elige un valor inicial para Pi. Por ejemplo, puedes elegir el valor 3.
- Utiliza una fórmula que involucre el valor de Pi para calcular un nuevo valor aproximado. Por ejemplo, puedes utilizar la siguiente fórmula: Pi = (Pi + (4 ÷ Pi)) ÷ 2
- Compara el nuevo valor aproximado con el valor anterior. Si la diferencia entre ambos es lo suficientemente pequeña, entonces has llegado a un resultado preciso. Si la diferencia es todavía grande, entonces asigna el nuevo valor a Pi y repite el proceso desde el paso 2.
Por ejemplo, si el valor inicial de Pi es 3, entonces el nuevo valor aproximado sería (3 + (4 ÷ 3)) ÷ 2 = 2,66666666. Pero, como la diferencia entre ambos no es muy pequeña, aún podrías repetir muchas veces el proceso antes de encontrar un valor preciso.
¿Cuáles son las aplicaciones del número Pi?
Pi es un número importante en matemáticas y tiene muchas aplicaciones en diversas áreas. Entre las aplicaciones más importantes de Pi, tenemos las siguientes:
Geometría
Pi se utiliza en la geometría para calcular el área y el perímetro de círculos y otras figuras circulares:
- Círculos: calcular el área y el perímetro de círculos.
- Esferas: determinar el área y el volumen de esferas.
- Cilindros: cálculo del área y el volumen de cilindros.
- Conos: se utiliza para calcular el área y el volumen de conos.
Trigonometría
Es útil en la trigonometría para calcular ángulos y longitudes de arcos. Algunas de sus aplicaciones son:
- Ángulos: calcular ángulos y longitudes de arcos.
- Funciones trigonométricas: se usa para calcular el valor de las funciones trigonométricas para ciertos ángulos.
- Trigonometría circular: para calcular los valores de las funciones trigonométricas para ángulos de 360 grados.
Ingeniería
En ingeniería, Pi se utiliza en el cálculo de magnitudes como el volumen y la capacitancia. Algunas de sus aplicaciones son:
- Electrónica: calcular magnitudes como la resistencia y la capacitancia.
- Electricidad: se emplea para calcular magnitudes como la potencia y la energía eléctrica.
- Ingeniería civil: calcular magnitudes como el área y el volumen de estructuras y elementos de construcción.
Física
El número Pi (π) es una constante matemática que tiene muchas aplicaciones en la física. Algunos ejemplos de cómo se utiliza Pi en física son:
- Ondas: se usa para calcular la frecuencia y la longitud de onda de las ondas.
- Mecánica: En la mecánica, es útil para el cálculo del trabajo y la energía en sistemas rotativos.
- Electromagnetismo: En electromagnetismo, se puede utilizar para calcular la energía almacenada en un capacitador y la inductancia en un bobinado.
- Cosmología: En cosmología, Pi se emplea para calcular la curvatura del espacio-tiempo y la expansión del universo.
¿Qué aplicaciones tiene el número Pi en la vida real?
Algunos ejemplos de cómo se utiliza Pi en la vida cotidiana son:
- Geometría: definir el área de una alfombra circular o para medir la longitud de la cinta métrica necesaria para cubrir el perímetro de una mesa circular.
- Cocina: determinar cuánta agua o líquido se necesita para llenar una olla o para saber cuántos ingredientes se pueden meter en un recipiente circular.
- Astronomía: conocer la distancia entre planetas y estrellas, la órbita de los planetas y la posición de los cuerpos celestes en el cielo.
- Jardinería: saber cuánto suelo o tierra se necesita para rellenar una maceta circular o para calcular cuánta agua se necesita para regar una planta en un jardín circular.