Seguro que has oído hablar del conjunto de los números imaginarios o de la unidad imaginaria. Es un concepto matemático que surge de la necesidad matemática de expresar números que no pertenecen a los números reales.
Contenido
¿Qué son los números imaginarios?
Los números imaginarios son aquellos que cuando se elevan al cuadrado dan un número negativo. En consecuencia, son valores equivalentes a la raíz cuadrada de un número negativo. Por ejemplo, la unidad imaginaria (el número i) es igual a la raíz cuadrada de -1.

Estos números no pertenecen a los reales, porque en el conjunto real, no se pueden resolver las raíces negativas. Es aquí donde radica la importancia del conjunto imaginario. Este conjunto se inventó para poder tratar con raíces negativas y poder resolver todas esas ecuaciones cuadráticas y problemas que «no tienen solución», porque nos dan una raíz negativa.
Para evitar confusiones es importante distinguir entre números imaginarios y números complejos. Los complejos son números que están formados por un número real y un número imaginario. Por lo tanto, los imaginarios son una subcategoría de los complejos, los cuales no tienen parte real. En la siguiente tabla, se puede apreciar mejor las diferencias.
| Número Complejo | Parte Real | Parte Imaginaria | Descripción |
| 4 + 7i | 4 | 7i | Complejo |
| 3 | 3 | 0 | Real Puro |
| 2i | 0 | 2i | Imaginario Puro |
Para acabar de situar este conjunto numérico, podemos visualizar en la siguiente imagen una estructura de todos los conjuntos. Como podemos ver, los números complejos abarcan todos los tipos de números, estos a su vez, pueden dividirse en los reales y en los imaginarios puros (que son los que estamos tratando en este artículo).

Ejemplos de números imaginarios
Partiendo de la unidad imaginaria (i), podemos deducir otros números imaginarios. Solamente, hay que aplicar la siguiente fórmula:
m = r · i
Donde, m es un número imaginario, r es un número real y i es la unidad imaginaria. En la siguiente imagen, puedes ver cómo obtenemos diferentes imaginarios a partir de raíces negativas.
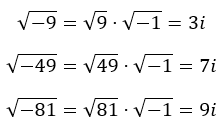
De hecho, podemos extrapolarlo a la siguiente expresión:
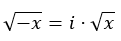
Propiedades de los números imaginarios
Los números imaginarios tienen una serie de propiedades muy interesantes. Algunas de las cuales ya las hemos comentado al principio de este artículo y algunas otras no:
- Los imaginarios no pertenecen al conjunto de los reales, pues son números que físicamente no existen y no pueden representarse en nuestra realidad.
- Son valores equivalentes a las raíces negativas.
- Pueden representarse gráficamente en la recta imaginaria.
- Las potencias imaginarias (es un concepto que explicaremos en el siguiente apartado), son de gran ayuda para simplificar los cálculos numéricos en los que intervienen valores imaginarios.
- La fórmula de Euler es una expresión que nos permite relacionar los números imaginarios con los reales.
Operaciones con los números imaginarios
Ahora ya conoces todas las características importantes de los números imaginarios, así que es hora de aprender a resolver operaciones con ellos. Para operar con imaginarios, debes seguir los mismos pasos que sigues cuando operas con valores reales, solo que debes tener en cuenta un concepto: las potencias imaginarias.
Potencias imaginarias
Los números imaginarios tienen una propiedad muy interesante que sucede cuando multiplicas la unidad imaginaria por sí misma. Dicho de otra manera, sucede cuando haces potencias de la unidad imaginaria. Si escribimos las potencias, tal como en la siguiente lista, se puede descubrir un patrón:
i0 = 1
i1 = i
i2 = i · i = (√-1) · (√-1) = -1
i3 = i2 · i = (-1) · i = -i
i4 = i2 · i2 = (-1) · (-1) = 1
Conocer este concepto es algo que nos va a facilitar mucho la resolución de operaciones con números imaginarios, porque podremos simplificar operaciones difíciles y hacerlas algo más sencillas. Además, lo bueno de estas potencias es que se repiten indefinidamente. Podemos verlo, si añadimos algunas potencias más:
i5 = i
i6 = -1
i7 = -i
i8 = 1
etc.
Y con las potencias negativas, también sucede esto.
Operaciones aritméticas con números imaginarios
A continuación, te vamos a plantear un ejemplo de cada operación aritmética básica, para que puedas ver cálculos de números imaginarios resueltos.
- Suma de números imaginarios: es exactamente igual que la suma de números reales, solo tienes que acordarte de añadir la i.
4i + 3i = 7i
- Resta de números imaginarios: las restas también se resuelven igual que en el conjunto real.
4i – 3i = i
- Multiplicación de números imaginarios: en este caso, debemos tener en mente las potencias imaginarias que hemos comentado antes.
3i · 4i = 12 · i2 = 12 · (-1) = -12
- División de números imaginarios: en este tipo de divisiones también tenemos que estar alertas, por si nos encontramos con alguna potencia imaginaria, que nos permita simplificar la operación.
12i ÷ 4i = 3
Ecuaciones con números imaginarios
Como hemos dicho antes, cuando resolvemos ecuaciones en el conjunto real, hay algunas veces que obtenemos raíces negativas y, por lo tanto, las ecuaciones «no tienen soluciones». Pero, ahora que conocemos los imaginarios, podemos resolver esas ecuaciones. Veamos un ejemplo:
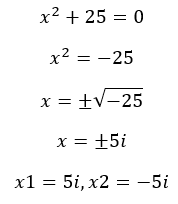
¿Para qué sirven los números imaginarios?
Los números imaginarios surgen de la necesidad de poder expresar valores que están fuera del conjunto real. Es por eso, que de primeras, puede parecer que no tienen muchas aplicaciones útiles. Pero, la verdad es que es justo al contrario. Porque, los cuando los combinamos con los reales, obtenemos los números complejos.
Y estos sí que tienen muchísimas aplicaciones. Se usan para estudiar la corriente alterna (porque tiene valores negativos), su uso también está muy extendido en el ámbito de las ondas (lo cual tiene aplicaciones en la física, la electrónica de telecomunicaciones y en la mecánica cuántica). Entre muchos otros usos.
Además, hay muchas veces que cuando resuelves una ecuación cuadrática, el valor te da una raíz negativa y no puedes operar… Con los imaginarios puedes resolverlas. Así que, a modo de conclusión, podemos decir que es un conjunto que nos permite expandir nuestros conocimientos más abstractos.