Las ecuaciones de primer grado o ecuaciones lineales son la base del álgebra, ya que si no las comprendes te será muy complicado entender ecuaciones más complejas. Entonces, la característica distintiva de este tipo de ecuaciones es que la parte literal de los monomios no puede tener exponente. Por lo tanto, en una ecuación lineal solo encontraremos monomios sin parte literal y monomios con parte literal sin exponente, como por ejemplo: 3 + x = -5 – 3x.
También destacar que estas ecuaciones suelen tener una única solución, aunque también pueden no tener ninguna. Para poder saber qué caso tenemos delante deberemos resolver la ecuación y al final analizar el resultado. De esta manera, si obtenemos una igualdad imposible como puede ser 2 = 0, entonces la ecuación no tiene solución. Por otro lado, si obtenemos una igualdad que siempre se cumple, entonces la solución equivale a todos los números reales. Y por último, si al final obtenemos la igualdad de X y un valor numérico, en ese caso tendremos un resultado único.
Contenido
Procedimiento de resolución de una ecuación lineal
Resolver una ecuación equivale a calcular el valor de una variable, representada por una letra (x, y, a, b…). Entonces, para poder encontrar ese valor debemos seguir los siguientes pasos:
- Resolver paréntesis y fracciones: para empezar eliminamos todos los paréntesis y denominadores, así conseguimos una ecuación más sencilla de entender. Porque podemos apreciar directamente qué términos están acompañados de la incógnita y cuáles no, esta lectura nos permite proseguir fácilmente con la resolución de la expresión.
- Simplificar la expresión: agrupamos los términos semejantes, (los términos independientes por un lado, y los términos con x por otro). Entonces, a un lado dejaremos los números que tengan la incógnita y los demás números los pasaremos al lado contrario. Pero recuerda que para poder cambiarlos de lado, deberemos cambiar su signo.
- Operar en cada lado: realizamos todas las operaciones en el siguiente orden: potencias/raíces, multiplicaciones/divisiones y sumas/restas. Hacemos esto hasta obtener un único término en cada lado y, por lo tanto, nos queda una ecuación con la misma estructura que esta: 4x = 8.
- Aislar la variable: finalmente, solo nos queda pasar el valor que acompaña a la letra dividiendo al otro lado y de esa manera hallamos su valor final. Al finalizar este paso ya habremos despejado la incógnita y sabremos qué tipo de resultado nos queda: una única solución, una solución no válida o una solución que se cumple con todos los enteros.
Ejemplos de ecuaciones de primer grado
A continuación, puedes encontrar ecuaciones de primer grado resueltas, las cuales están organizadas en distintas categorías según la complejidad de su estructura. Entonces, conociendo el procedimiento teórico para resolver ecuaciones lineales y los diferentes tipos que existen, ya tendrás el conocimiento necesario para poder solucionarlas fácilmente y empezaremos con la práctica. Dicho esto, empecemos con la explicación teórica:
Ecuaciones de primer grado básicas
Este primer tipo de ecuaciones lineales solamente están compuestas por las operaciones aritméticas básicas (sumas, restas, multiplicaciones y divisiones). A continuación te mostramos dos ejemplos resueltos, el primero es un poco más básico y el segundo es un poco más complejo en cuanto a cálculo:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3 / 2
Ecuaciones de primer grado con paréntesis
En segundo lugar, tenemos las ecuaciones lineales con paréntesis. Estas son algo más complicadas de resolver que las anteriores, aunque su única dificultad está en el cálculo, ya que debes respectar las propiedades de los paréntesis. Para que quede más claro, te mostramos dos ejemplos resueltos:
2 (x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11 / 19
Ecuaciones de primer grado con potencias y raíces
El tercer nivel es bastante sencillo, ya que solamente añade potencias y raíces. La única dificultad que puedes encontrarte con estas ecuaciones es cuando el exponente o la raíz afecta a un paréntesis entero (como el segundo ejemplo que te mostraremos), pero todo lo demás sigue siendo más o menos igual. A continuación puedes encontrar dos ejemplos.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Ecuaciones de primer grado con fracciones
La última categoría de ecuaciones lineales que podemos encontrar es esta, la cual está compuesta por todos los elementos que hemos ido comentando anteriormente y además, por fracciones. Este nivel es el más complejo y hay varios métodos para resolverlas. El primero y más fácil es pasar multiplicando los denominadores al lado contrario del igual, aunque solo podemos utilizarlo cuando tenemos dos fracciones. Por otro lado, si tenemos más de dos fracciones dentro de la ecuación, entonces deberemos encontrar un denominador común y multiplicar todas las fracciones por la división de ese valor entre el denominador de la misma fracción. A continuación puedes encontrar un ejemplo de cada tipo:
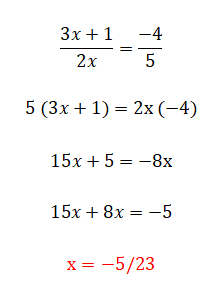
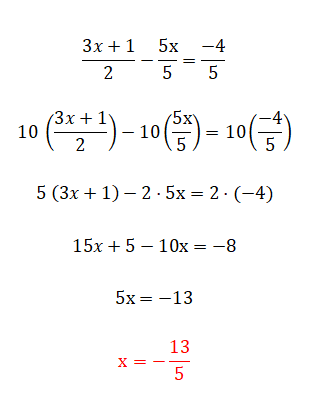
Ejercicios de ecuaciones de primer grado
Ahora, te planteamos algunos ejercicios de ecuaciones lineales. Están organizados según una dificultad creciente, con lo cual las primeras ecuaciones son más fáciles que las últimas. Por eso, te recomendamos que empieces desde el principio y veas hasta dónde puedes llegar. Entonces, trata de resolver las siguientes ecuaciones, y después compara tu resultado con las soluciones que te proporcionamos.
Primer ejercicio
El primer ejercicio es una ecuación lineal muy sencilla, ya que solamente está formada por sumas y restas, además solamente tiene cuatro términos entre los dos lados de la igualdad:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- Agrupamos los términos semejantes.
- Simplificamos ambos lados.
- Despejamos la incógnita y calculamos su valor.
Segundo ejercicio
En este caso nos encontramos con una ecuación formada por paréntesis, con lo cual nuestra máxima prioridad es eliminarlos, para después poder agrupar los términos semejantes:
-4 (x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- Resolvemos el paréntesis.
- Movemos las x a la izquierda y los términos independientes a la derecha.
- Despejamos la incógnita.
Simplificamos el resultado.
Tercer ejercicio
A continuación deberás resolver otra ecuación de primer grado con paréntesis, aunque esta es algo más difícil. Esto se debe a que cuenta con paréntesis anidados (paréntesis dentro de otros). Por lo tanto, deberás seguir correctamente el orden de resolución: primero los de dentro y luego los de fuera.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28 / 3
- Empezamos resolviendo los paréntesis interiores.
- Después, resolvemos los paréntesis externos.
- Simplificamos ambos lados de la igualdad y agrupamos términos semejantes.
- Aislamos x y calculamos su valor.
Cuarto ejercicio
En este ejercicio empezamos a ver fracciones, las cuales son posiblemente el elemento más complicado dentro de las ecuaciones lineales. Aunque no te preocupes porque si te has leído la teoría, sabrás perfectamente cómo proceder:
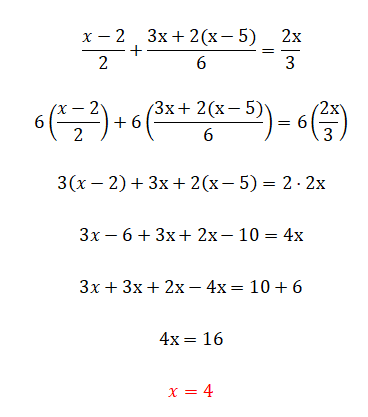
Quinto ejercicio
En este quinto ejercicio nos aparecen fracciones con paréntesis, lo cual quiere decir que la jerarquía de resolución se complica un poco. Cabe mencionar que este ejemplo se puede resolver por medio de dos métodos: usando el método del mínimo común múltiplo u operando directamente con las fracciones. A continuación puedes ver los dos procedimientos completos:
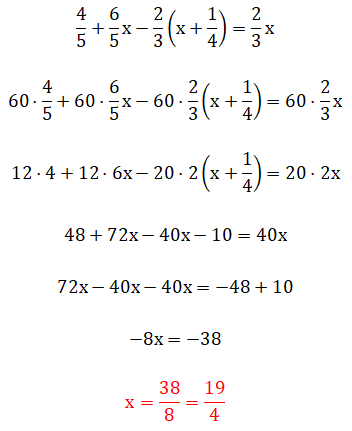
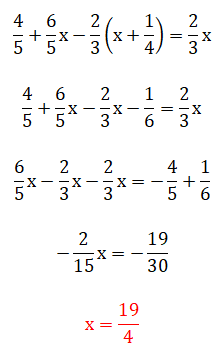
Sexto ejercicio
A continuación vamos un poco más allá con el tema de las fracciones y los paréntesis, ya que tenemos paréntesis anidados. Este ejercicio no aporta muchas más complicaciones respecto al anterior, sencillamente es un poco más difícil en cuanto a cálculos y ya está.
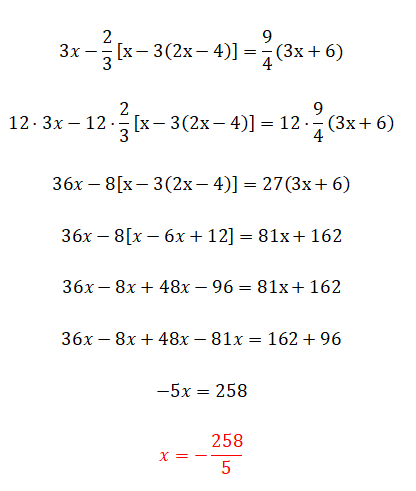
- Multiplicamos todos los términos por el mcm de los denominadores.
- Simplificamos la expresión eliminando los paréntesis: primero los internos y después los externos.
- Agrupamos términos semejantes a cada lado.
- Resolvemos las operaciones en cada lado.
- Y calculamos el valor de la incógnita.
Séptimo ejercicio
El siguiente ejercicio puede parecer muy fácil, pero te recomendamos que pruebes de resolverlo igual, ya que seguramente te da un resultado algo peculiar. Después de que lo hayas probado mira la solución y la explicación que hay debajo del ejercicio.
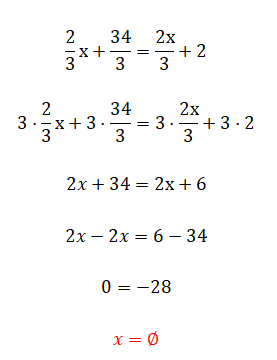
- Multiplicamos todas las fracciones con el mcm de los denominadores.
- Simplificamos la expresión obtenida.
- Y finalmente vemos que nos da una igualdad falsa, ya que hemos eliminado la incógnita.
Como habrás notado, es una igualdad falsa o igualdad sin resultado, ya que no hay ningún valor que complete la ecuación correctamente. Este es uno de los casos que hemos comentado en la introducción.
Octavo ejercicio
Por último, te proponemos este ejercicio, el cual es bastante complicado porque tiene todas las complicaciones que hemos visto a lo largo de este artículo, aunque también tiene un pequeño truco. Comentar que si eres capaz de resolver esta ecuación de primer grado, entonces has entendido toda la teoría perfectamente. Y si no, no te preocupes, porque este ejercicio es bastante complicado.
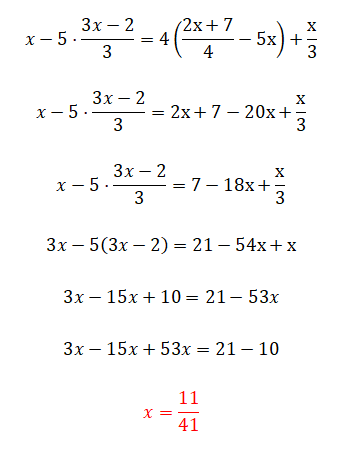
- Empezamos eliminando los cuatros que hay en el lado derecho de la igualdad.
- Después juntamos las x de la parte derecha.
- Multiplicamos por tres todos los términos, para poder eliminar los denominadores.
- Eliminamos el paréntesis.
- Juntamos los términos semejantes.
- Calculamos el valor de la incógnita.
Más ejercicios de ecuaciones lineales
Ahora que ya has practicado bastante deberías ser capaz de resolver ecuaciones lineales complejas. Aunque si quieres seguir practicando, te recomendamos que pruebes de resolver esta ficha de ejercicios. Pero si crees que ya has repasado suficiente, también podemos ofrecerte un artículo que te puede ayudar a entender la jerarquía de operaciones. De esta manera, sabrás qué cálculo resolver primero en todo momento y nunca te equivocarás.