Una ecuación de segundo grado o ecuación cuadrática es una ecuación de grado 2, con lo cual el mayor exponente que tiene cualquiera de sus términos es igual a 2. Esto quiere decir que la ecuación puede tener hasta dos soluciones distintas, aunque también puede tener una única solución o directamente no tener ninguna.
Para calcular las soluciones o raíces de ecuaciones de segundo grado podemos seguir dos procedimientos diferentes: por medio de la fórmula cuadrática o factorizando la expresión. En este artículo hablaremos sobre los dos métodos y te plantearemos algunos ejercicios de práctica. Aunque antes aclararemos algunos conceptos para que toda la explicación se entienda muy bien y saques un mayor provecho de la lectura.
Contenido
Tipos de ecuaciones de segundo grado
La principal categorización entre las ecuaciones cuadráticas es según la estructura de la misma expresión. Entonces, la estructura estándar o habitual de estas expresiones es la siguiente: ax² + bx + c. Esta forma común equivale a una ecuación completa, pero cuando hay términos nulos o iguales a cero, entonces la estructura puede variar, es aquí donde aparecen las ecuaciones incompletas. A continuación, te explicaremos las características de todos los tipos en mayor detalle.
Ecuaciones de segundo grado completas
Como ya hemos dicho, tenemos las ecuaciones cuadráticas completas, estas tienen todos los coeficientes a, b y c diferentes a cero. Por lo tanto, la expresión sigue al pie de la letra la estructura ax² + bx + c, ya que tiene todos los términos: el término de segundo grado, el término lineal y el término independiente. Un ejemplo de este tipo es la ecuación siguiente: x² + 2x + 1 = 0.
Ecuaciones de segundo grado incompletas
En cuanto a las ecuaciones incompletas las podemos distinguir según qué coeficiente es igual a cero. Recuerda que si esta explicación no te resuelve tus dudas, justo debajo hay una imagen en la cual puedes encontrar todos los casos explicados paso por paso.
- Ecuaciones incompletas (b = 0): en esta primera situación nos encontramos con una expresión que sigue la siguiente estructura: ax² + c = 0. Con lo cual, obtenemos dos resultados: el negativo y el positivo de la raíz de la fracción c / a.
- Ecuaciones incompletas (c = 0): cuando tenemos la forma ax² + bx = 0 debemos factorizar la ecuación para que nos quede la expresión x (ax + b) = 0. Por lo tanto, nos quedarán dos soluciones: x = 0 y x = -b / a.
- Ecuaciones incompletas (b = c = 0): en este caso tenemos una ecuación ax² = 0 y solamente tenemos una solución posible, la cual es x = 0.
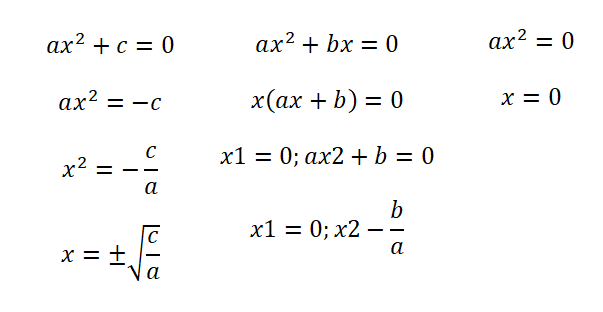
Cabe mencionar que los procedimientos que te hemos enseñado sirven para ir más deprisa a la hora de resolver ecuaciones incompletas. Pero, en todos los casos puedes utilizar la fórmula cuadrática que te enseñaremos más abajo, solamente deberás escribir un cero en los coeficientes que no existen.
Fórmula para ecuaciones de segundo grado
Para resolver las ecuaciones cuadráticas (ax² + bx + c = 0) deberemos, aplicar la fórmula general o fórmula cuadrática y después deberemos sustituir los valores numéricos que corresponden a cada letra en la expresión matemática.

También, es importante explicar que el de discriminante (Δ) es la expresión b² – 4ac, la cual se encuentra debajo de la raíz cuadrada. A partir de este concepto matemático podemos saber cuántas soluciones tiene esa ecuación de segundo grado. Básicamente, hay tres opciones: el discriminante es negativo (no hay soluciones reales), el discriminante es igual a cero (hay una sola solución) o el discriminante es positivo (hay dos soluciones).
Ejemplo de una ecuación cuadrática completa resuelta
Prueba de resolver la ecuación de segundo grado siguiente: 2x²+4x-6=0 y comprueba tu resultado con el de abajo. Te recomendamos que sigas el siguiente procedimiento: analizar el tipo de ecuación (identificar los términos nulos), calcular el discriminante para saber cuántas soluciones existen y finalmente, resolver la ecuación planteada con la fórmula.
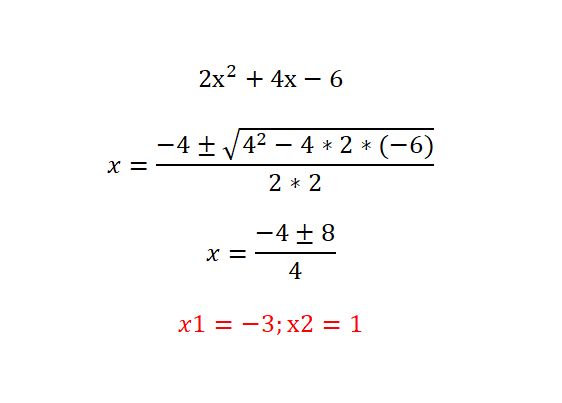
Demostración de la fórmula cuadrática
Si quieres saber de dónde viene la fórmula general de las ecuaciones de segundo grado, te recomendamos que veas el vídeo:
Factorizar ecuaciones de segundo grado
El segundo método que tenemos para resolver ecuaciones de segundo grado es la factorización. Entonces, para factorizar un polinomio (en nuestro caso un polinomio cuadrático), podemos usar diferentes métodos. Aunque por lo general, cuando se trata de ecuaciones de este estilo, suelen ser factorizables por un término en común. Y si ese no es el caso, entonces puedes probar aplicando las identidades notables, pero de normal no necesitarás saber otros métodos en estas situaciones.

Ejercicios de ecuaciones de segundo grado con soluciones
A continuación puedes encontrar una serie de ejercicios de ecuaciones de segundo grado completas e incompletas. De esta manera repasarás toda la teoría explicada a lo largo de este artículo y te quedará más claro cómo aplicarla en los ejercicios. Te recomendamos que trates de resolverlos por tu cuenta y solo mires la solución cuando los hayas acabado o cuando estés atascado. Dicho esto, ya puedes empezar a resolver los ejercicios.
Ejercicio 1
Resuelve la ecuación de segundo grado siguiente:
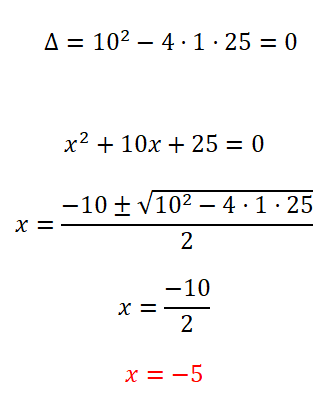
- Empezamos calculando el discriminante, para saber el número de soluciones posibles.
- Como es una ecuación cuadrática completa, aplicamos la fórmula cuadrática y resolvemos los cálculos.
- Obtenemos el valor de la incógnita x.
Ejercicio 2
Resuelve la ecuación cuadrática siguiente:
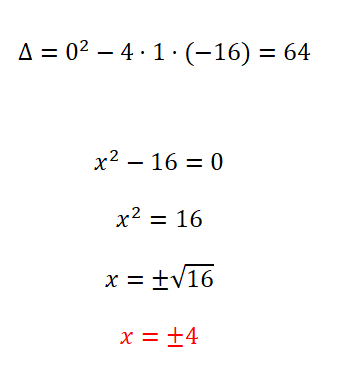
- Empezamos calculando el discriminante.
- Como tenemos una ecuación de segundo grado incompleta en que b = 0, aplicamos la norma para las ecuaciones de este tipo.
- Resolvemos el cálculo para obtener el resultado, y no podemos olvidar el signo ±.
Ejercicio 3
Resuelve la ecuación de segundo grado desordenada siguiente:

- Empezamos calculando el discriminante de la ecuación.
- Antes de poder aplicar la fórmula debemos ordenar la ecuación según la estructura ax² + bx + c = 0.
- Después aplicamos la fórmula general.
- Y finalmente obtenemos los resultados.
Ejercicio 4
Resuelve la siguiente ecuación de segundo grado por medio de la factorización:

- Antes que nada calculamos el discriminante.
- Después extraemos factor común de x.
- Entonces la primera solución es x = 0.
- Y la segunda es x = 3 / 2.
Ejercicio 5
Resuelve la ecuación cuadrática completa que te planteamos a continuación:

- Como siempre, calculamos el discriminante para saber cuántas soluciones tiene la ecuación en cuestión.
- Después aplicamos la fórmula cuadrática, ya que es una ecuación completa.
- Finalmente, expresamos el resultado de la ecuación.
Ejercicio 6
Resuelve la ecuación cuadrática con fracciones que te planteamos:

- Empezamos calculando el discriminante de la expresión.
- Después aplicamos la fórmula cuadrática, teniendo en cuenta que el coeficiente «a» está formado por una fracción.
- Resolvemos el cálculo.
- Y ya tenemos las dos raíces de la ecuación.
Ejercicio 7
Resuelve la siguiente ecuación de segundo grado:

- Empezamos calculando el discriminante.
- Antes de aplicar la fórmula tenemos que simplificar la expresión y darle la forma ax² + b + c = 0.
- Sustituimos todos los coeficientes en la fórmula y resolvemos el cálculo.
- Finalmente, obtenemos el resultado.
Ejercicio 8
Prueba de resolver la ecuación de segundo grado siguiente:
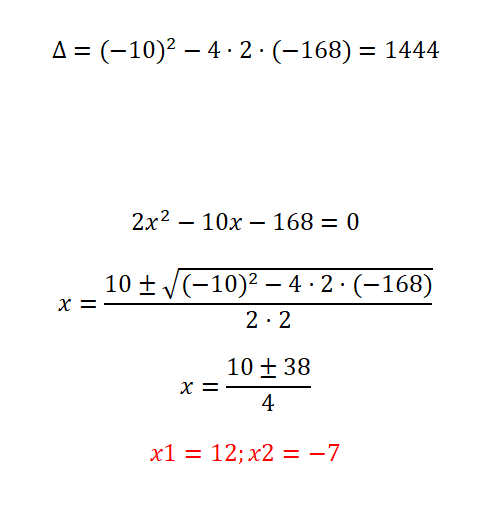
- Empezamos calculando el discriminante.
- Como se puede ver es una sencilla ecuación de segundo grado, aunque tiene unos coeficientes bastante grandes. Por lo tanto, tenemos que aplicar la fórmula y vigilar a la hora de hacer las operaciones.
- Al final obtenemos las dos soluciones posibles.