Los sistemas de ecuaciones son conjuntos de dos o más ecuaciones que tienen más de una incógnita. Entonces, para poder resolver sistemas podemos usar cuatro métodos: sustitución, igualación, reducción y graficación. Pero, antes de empezar a explicar los procedimientos de resolución, vamos a definir los tipos de sistemas que existen según el número de soluciones:
- Sistema compatible determinado: solo tiene una solución y podemos representarlo por dos rectas que se cruzan en un solo punto (el cual es la solución).
- Sistema compatible indeterminado: tiene infinitas soluciones y lo cual se debe a que son dos rectas que coinciden en los mismos puntos.
- Sistema incompatible: no tiene ninguna solución, ya que, las rectas son paralelas y, por lo tanto, no tienen ningún punto en común.
Contenido
Métodos para resolver sistemas de ecuaciones lineales
Ahora explicaremos los distintos sistemas que podemos usar para resolver sistemas de ecuaciones. En las explicaciones encontrarás teoría y algunos ejemplos, gracias a los cuales todos los conceptos explicados quedarán más claros. Cabe destacar que en este artículo solamente hablaremos sobre sistemas de ecuaciones 2×2, lo cual quiere decir que simplemente trataremos sistemas que estén compuestos por dos ecuaciones. Dicho esto, empecemos con la explicación.
Método de sustitución
El método de sustitución consiste en despejar una de las incógnitas en una de las ecuaciones y después sustituir la expresión obtenida, en la ecuación contraria. Este método es el más recomendable cuando al menos una de las incógnitas tiene el valor del coeficiente igual a 1. Entonces, los pasos a seguir son muy sencillos:
- Aislar una incógnita de alguna de las dos ecuaciones.
- Sustituir en la otra ecuación la expresión equivalente a la incógnita que hemos despejado de la primera ecuación.
- Despejar la incógnita contraria en la ecuación que hemos obtenido.
- Una vez tenemos el valor de la primera variable, deberemos usarlo para encontrar la segunda.

Método de igualación
El método de igualación se basa en aislar la misma variable en ambas ecuaciones y después igualar las dos expresiones obtenidas. Este método se recomienda cuando la misma incógnita se puede aislar sin dificultad en ambas ecuaciones, ya que facilita todo el cálculo. El procedimiento que debes seguir en este caso es el siguiente:
- Aislamos la incógnita que hemos escogido en las dos ecuaciones.
- Igualamos las expresiones equivalentes a esa incógnita.
- Resolvemos la ecuación con normalidad.
- Calculamos la otra incógnita con el valor que hemos calculado.

Método de reducción
El método de reducción se basa en multiplicar ambas ecuaciones por dos números, los cuales nos permitan obtener un mismo coeficiente con diferente signo de una de las variables en las dos expresiones. Este método es el más recomendable cuando una misma incógnita tiene el mismo coeficiente en todas las ecuaciones o en el caso de tener los mismos coeficientes con signos opuestos. Y el procedimiento de resolución es el siguiente:
- Se multiplican las dos ecuaciones por los números que sean necesarios (debemos encontrar dos números que nos permitan obtener en las dos ecuaciones un mismo coeficiente para una de las dos variables, pero, con signo contrario).
- Después, se restan o suman las ecuaciones para eliminar esa incógnita con sus respectivos coeficientes.
- Seguidamente, se resuelve la ecuación que nos ha quedado.
- Y utilizamos el resultado de esa ecuación, para obtener el valor numérico que nos falta de la otra variable.
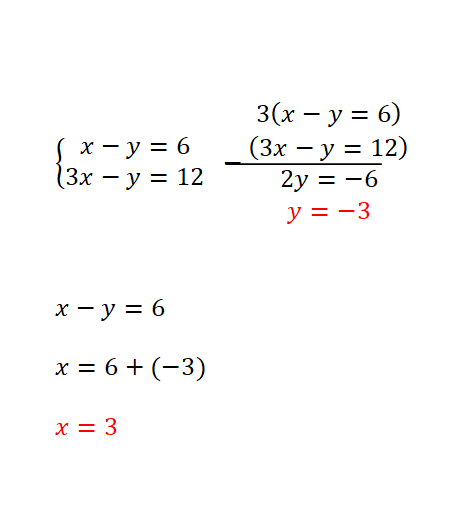
Método gráfico
Por último, podemos optar por resolver un sistema de ecuaciones por medio de la representación gráfica. Este método es bastante diferente a los demás, ya que no tiene una parte matemática compleja, es casi todo gráfico. Entonces, para conocer los valores de las incógnitas tenemos que estructurar las dos ecuaciones con la forma de la ecuación de la recta: y = mx + b. De esta manera podremos hacer la representación y después, asociaremos los valores de las coordenadas del punto de corte entre las dos funciones a las incógnitas. A continuación te mostramos un ejemplo resuelto:

Como se puede ver en la gráfica, el punto de corte entre ambas funciones es el (0, -3). Por lo tanto, el valor de x = 0 y el valor de y = -3. Así es como se resuelve un sistema de ecuaciones de manera gráfica.
¿Cómo resolver un sistema de ecuaciones de segundo grado?
Para resolver sistemas de ecuaciones cuadráticas podemos usar los métodos que acabamos de comentar. Personalmente, nos gusta recomendar el método de sustitución, ya que nos permite obtener una ecuación con una sola incógnita rápidamente. Por otro lado, si empleamos los métodos de reducción o igualación, el cálculo se nos complica bastante. Entonces, una vez has sustituido una de las dos variables, solamente tienes que resolver la ecuación de segundo grado o la ecuación de primer grado que resultante. A continuación, te planteamos un ejemplo para que veas todo el proceso:
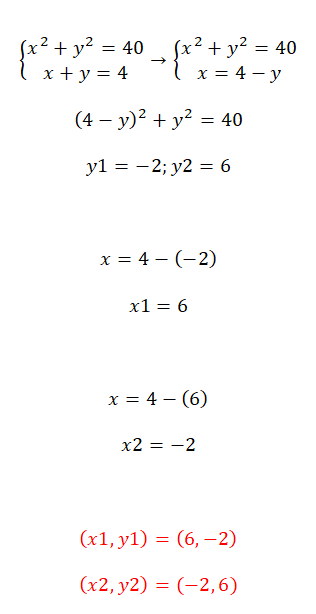
Ejercicios de sistemas de ecuaciones resueltos
Ahora te planteamos unos cuantos ejercicios de sistemas de ecuaciones lineales y de segundo grado para que apliques la teoría explicada. De este modo, entenderás mejor todos los conceptos relacionados con el cálculo de sistemas de ecuaciones. Te recomendamos que pruebes de resolverlos antes de mirar las respuestas que te ofrecemos, así sacarás más provecho a los ejercicios:
Ejercicio 1
Resuelve este sistema de ecuaciones usando el método de sustitución:

- Empezamos despejando una de las dos incógnitas en una ecuación.
- Después sustituimos la expresión obtenida en la ecuación contraria, por la incógnita que hemos despejado previamente.
- Entonces obtenemos el resultado de la variable contraria.
- Seguidamente, sustituimos el primer valor descubierto en cualquiera de las dos ecuaciones para calcular el valor de la primera incógnita.
- Finalmente, expresamos el resultado de ambas variables.
Ejercicio 2
Resuelve este sistema de ecuaciones usando el método de sustitución:
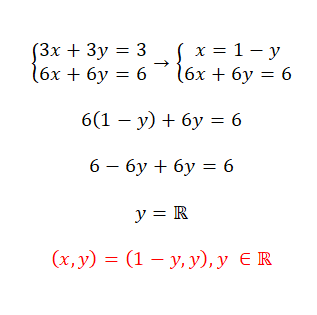
- En este caso seguiremos el mismo procedimiento: aislar una incógnita, sustituirla en la otra expresión y aislar la segunda variable.
- Como podemos ver este es un sistema compatible indeterminado, ya que tiene infinitas soluciones.
Ejercicio 3
Resuelve este sistema de ecuaciones usando el método de igualación:

- El primer paso es aislar la misma variable en las dos ecuaciones, en este caso hemos elegido la x.
- Seguidamente, igualamos las expresiones obtenidas y empezamos a resolver.
- Entonces, obtenemos el valor de la primera incógnita.
- Y si lo sustituimos en alguna de las dos ecuaciones originales, podemos calcular la segunda incógnita.
- Finalmente, expresamos el resultado de ambas variables.
Ejercicio 4
Resuelve este sistema de ecuaciones usando el método de igualación:

- Primero de todo despejamos la x en ambas ecuaciones.
- Después igualamos las expresiones que hemos obtenido.
- Obtenemos el valor de la primera incógnita.
- Sustituimos ese valor en alguna de las dos ecuaciones iniciales y calculamos la segunda incógnita.
- Finalmente, expresamos el valor de ambas incógnitas.
Ejercicio 5
Resuelve este sistema de ecuaciones usando el método de reducción:
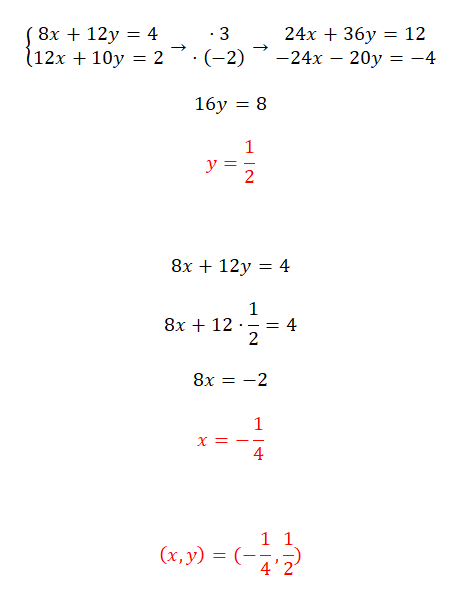
- Tenemos que buscar dos números que nos permitan obtener en las dos ecuaciones un mismo coeficiente para una de las dos variables, pero, con signo contrario.
- Después, solamente tenemos que resolver la ecuación que obtenemos al sumar las dos expresiones obtenidas.
- Seguidamente, sustituimos la y en alguna de las dos ecuaciones iniciales, para calcular la x.
- Finalmente, expresamos el resultado del sistema.
Ejercicio 6
Resuelve este sistema de ecuaciones usando el método de reducción:
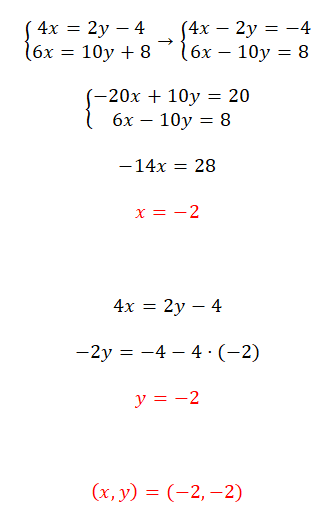
- Empezamos arreglando las ecuaciones (pasando todas las variables a la izquierda).
- Después multiplicamos por -5 la primera ecuación.
- Resolvemos la ecuación que obtenemos de sumar ambas ecuaciones y obtenemos el valor de x.
- Usamos este valor conocido para obtener el de y.
- Expresamos el resultado del sistema de ecuaciones.
Ejercicio 7
Resuelve este sistema de ecuaciones usando el método de sustitución:
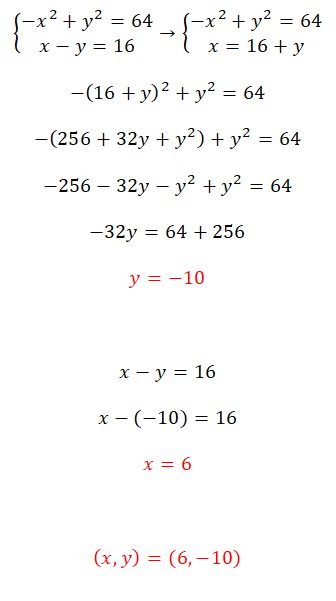
- Para resolver este sistema de ecuaciones no lineales, te recomendamos que uses el método de sustitución.
- Entonces, construyes una ecuación con la expresión equivalente a la x.
- Obtienes el valor de la incógnita y.
- Calculas el valor de x con el valor que has calculado previamente.
- Y ya tienes los dos valores.
Ejercicio 8
Resuelve este sistema de ecuaciones usando el método que prefieras:

- En este caso se nos plantea un sistema compatible determinado y nosotros lo vamos a resolver a través del método de igualación.
- Por lo tanto, despejamos la x en ambas ecuaciones e igualamos las dos expresiones resultantes.
- Después de resolver la ecuación obtenemos el valor de la y.
- Usamos ese valor para encontrar el de x.
- Finalmente, expresamos el resultado del sistema.