Las fracciones o números fraccionarios son expresiones numéricas que indican una cantidad dividida entre otra. Por lo tanto, es un valor representado por el cociente de dos números. Con este tipo de números podemos expresar cantidades decimales y enteras e incluso podemos indicar proporciones. A continuación, definiremos las fracciones de una manera más matemática y te mostraremos algunos ejemplos, para que entiendas gráficamente este concepto.
Contenido
¿Qué son las fracciones?
Una fracción equivale a la cantidad de partes que cogemos de una unidad que está dividida en partes iguales. Entonces, gráficamente se representa con dos términos separados por una línea horizontal en medio. Concretamente, en la parte superior de la línea encontramos el numerador y debajo el denominador.
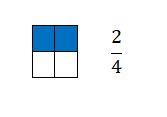
Como se puede ver, las fracciones son un concepto matemático muy fácil de representar gráficamente, ya que van de la mano con las proporciones. Es por eso que en el ejemplo anterior hemos expresado el número de cuadrados coloreados con un número fraccionario.
Términos de la fracción
Las dos partes de la fracción son:
- Numerador: este término está situado por encima de la línea horizontal y es donde escribimos el número de partes que tomamos. Podemos encontrar numeradores positivos, negativos y nulos (iguales a cero).
- Denominador: este otro término está situado debajo de la línea y es donde escribimos el número total de partes en que está dividida la unidad. Podemos encontrar denominadores positivos y negativos, pero estos no pueden ser nulos.
Tipos de fracciones
Existen muchas clases de fracciones diferentes, según los números que la conforman y según la equivalencia que presentan con otras fracciones. A continuación, definiremos todas las categorías que existen y comentaremos las características que nos permiten diferenciarlas de las demás:
- Fracciones propias: son aquellas que están formadas por un numerador que es menor que el denominador. Si conviertes estas fracciones a un número decimal, obtendrás una cifra entre el cero y el uno. No podrá ser mayor que uno, ya que el valor del numerador será siempre más pequeño que el del denominador y, por lo tanto, no se superará la unidad.
- Fracciones impropias: son aquellas que tienen un numerador mayor que el denominador, en este caso expresan valores numéricos mayores a la unidad. Como por ejemplo, 8/5 equivale a 1,6 lo cual es más grande que 1. Estas son otra manera de expresar números mixtos, los cuales son el siguiente tipo.
- Fracciones mixtas: también conocidas como números mixtos son aquellas que están compuestas por un número entero y otro fraccionario. Básicamente, se representan con el valor entero delante de la fracción, entonces para convertirlas en fracciones impropias debes multiplicar la parte entera por el denominador, sumarla al numerador y dejar el mismo denominador.
- Fracciones decimales: son aquellas que tienen un denominador que expresa una cantidad equivalente a una potencia de diez, por ejemplo: 6/10, 34/1000 o 5/100. Estas se utilizan en la notación decimal y son las más comunes a la hora de convertir números decimales exactos en números fraccionarios, esto lo comentaremos en mayor profundidad en el siguiente apartado.
- Fracciones compuestas: son aquellas que están compuestas por otra fracción, ya sea en el numerador, en el denominador o en ambos. Entonces, para simplificar estas expresiones y mostrarlas en una sola fracción, tenemos que dividir el numerador entre el denominador. Esto quedará más claro una vez expliquemos la división entre fracciones.
- Fracciones equivalentes: son aquellas que equivalen a un mismo número, aunque no estén formadas por los mismos numeradores ni denominadores. Por ejemplo, 8/4 = 4/2 = 2, ambas fracciones son equivalentes a dos. En este caso en concreto se debe a que la primera fracción es igual al doble de la segunda, por lo tanto, mantiene una relación proporcional.
- Fracciones irreducibles: son aquellas que no se pueden simplificar más, esto se debe a que el numerador y el denominador no comparten factores en común y, como resultado no se pueden dividir entre ningún número. Algunos ejemplos de este tipo son: 9/5, 5/6, 7/8, entre otros. Para saber detectarlas es importante saber calcular el máximo común divisor.
Operaciones con fracciones
Ahora que ya sabemos las diferentes categorías de fracciones que existen, vamos a ver cómo resolver las diferentes operaciones aritméticas con los números fraccionarios. Cabe destacar que es algo más complicado que las operaciones con números enteros, aunque una vez entiendes la metodología todo es bastante fácil. Además, no solo explicaremos la teoría, sino que también te mostraremos algunos ejemplos. Dicho esto, empezamos.
Suma de fracciones
La suma de fracciones con denominador común es bastante sencilla, ya que solamente hace falta sumar los dos numeradores y dejar el mismo denominador. Por otro lado, la suma de fracciones con distinto denominador se complica un poco, porque tienes que encontrar el mínimo común múltiplo de los denominadores. Y después, tienes que sumar el producto de cada numerador por la división del mcm (el nuevo denominador) entre el antiguo denominador. Para que se entienda mejor puedes mirar el siguiente esquema:
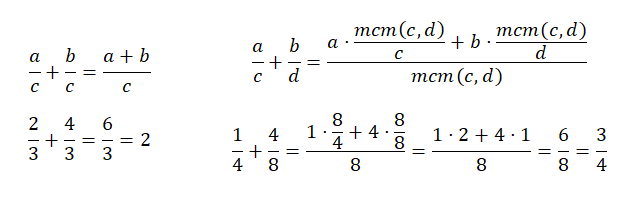
Resta de fracciones
La resta de fracciones con denominador común es muy similar a la suma, de hecho se hace todo igual excepto en la suma de los numeradores, porque en vez de sumar tienes que restar. Y en la resta de fracciones con distinto denominador pasa lo mismo, es prácticamente igual excepto que en vez de sumar el producto de los numeradores por la división del mcm entre el antiguo denominador, tienes que restar. A continuación te mostramos otro esquema:
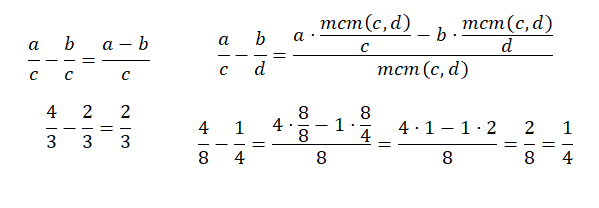
Multiplicación de fracciones
La multiplicación de fracciones se puede resolver de la misma manera independientemente de si los denominadores son iguales o no. Básicamente, tienes que multiplicar los numeradores por una parte y los denominadores por otra. Esta es posiblemente la operación más sencilla, ya que solo tienes que efectuar dos multiplicaciones.

División de fracciones
La división de fracciones es también bastante sencilla de resolver, solamente tienes que multiplicar en cruz. Dicho de otro modo, el numerador es el resultado de multiplicar el numerador de la primera fracción por el denominador de la segunda. Mientras que el denominador es el producto del denominador de la primera fracción y del numerador de la segunda.

Simplificación de fracciones
Simplificar fracciones o reducir fracciones no es como tal una operación aritmética, pero es muy importante saber hacerlo y además, es un tema que ya hemos tocado un poco con los tipos de fracciones. Entonces, para simplificar un número fraccionario tenemos que dividir tanto el numerador como el denominador entre un mismo número. Generalmente, elegiremos el máximo común divisor para hacer esta simplificación. En la siguiente imagen puedes encontrar un ejemplo.
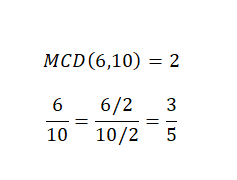
Como se puede ver, tenemos dos fracciones equivalentes, con lo cual ambas representan el mismo valor numérico, pero la segunda es más simple que la primera. Por lo tanto, hemos conseguido el objetivo de la simplificación con éxito.
¿Cómo pasar de decimal a fracción y viceversa?
La fracción generatriz es la fracción irreducible que se obtiene a partir de un número decimal, ya sea un decimal exacto o un decimal periódico. Claro está que deberemos usar diferentes métodos según el tipo de decimal, es exactamente lo que vamos a comentar a continuación.
Pasar de decimal exacto a fracción generatriz
En este caso, podemos recurrir a las fracciones decimales que hemos comentado al principio. Sencillamente, tenemos que escribir en el numerador el valor numérico, pero sin la coma. Mientras que en el denominador escribimos la potencia de diez que tenga tantos ceros como cifras tenga el numerador.
Aunque, si tenemos un número decimal mayor que la unidad, como puede ser el 4,25, entonces tendremos que multiplicar el número de unidades completas que tenemos por el valor del denominador y sumarlo al numerador original. A continuación, puedes encontrar un ejemplo de cada tipo:
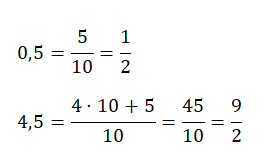
Pasar de decimal periódico puro a fracción generatriz
Cuando tenemos un número decimal periódico puro, si queremos obtener la fracción generatriz tendremos que poner en el numerador el mismo valor, pero sin coma decimal y restarle la parte entera. Mientras que el denominador será igual a un número formado únicamente por nueves, concretamente deberemos escribir tantos nueves como la cantidad de cifras que tenga la parte decimal del número original. Este sistema es algo confuso, pero con un par de ejemplos se entenderá:
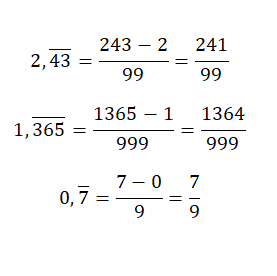
Pasar de decimal periódico mixto a fracción generatriz
En caso de tener un número decimal periódico mixto, tendremos que aplicar una norma bastante compleja. Primeramente, escribiremos en el numerador el número sin la coma decimal y le restaremos la parte entera seguida de los decimales no periódicos, también sin coma decimal. En cuanto al denominador, tendremos que escribir tantos nueves como cifras tenga la parte decimal periódica, seguido de tantos ceros como cifras tenga la parte decimal no periódica.

Pasar de fracción a decimal
Para pasar de una fracción a un decimal solamente hay que dividir el numerador entre el denominador, ya que un número fraccionario no es más que el cociente entre dos valores. Así que, resolviendo la división obtienes el número decimal correspondiente. En la siguiente imagen puedes encontrar algunos ejemplos bastante sencillos:
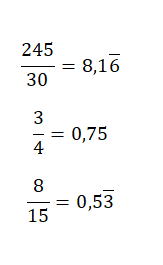
Ejercicios de fracciones
Ahora que ya sabes toda la teoría acerca de las fracciones, te recomendamos que hagas algunos ejercicios. De esta manera, aprenderás todos los conceptos explicados con mayor profundidad y el día del examen irás más rápido resolviendo los cálculos. Además, habrás visto todos los tipos de ejercicios de fracciones que hay y sabrás cómo resolverlos en consecuencia. Por último, comentarte que también tenemos a tu disposición una calculadora de fracciones online, con la cual podrás resolver todas las operaciones de fracciones.
