Productos notables

¿Qué son los productos notables o identidades notables?

Las identidades notables, también llamadas productos notables o igualdades notables, son unos recursos matemáticos que nos permiten resolver productos y cocientes de polinomios con más rapidez. Tal como indica la palabra identidad, se trata de igualdades que nos permiten calcular estas operaciones sin tener que resolverlas de verdad. Ya que sabemos que esa expresión sigue unas reglas fijas (que siempre se cumplen) y, por lo tanto, podemos obtener el resultado sin necesidad de verificarlo.

¿Cuándo usar una identidad notable?

Estas identidades se utilizan mayormente en el ámbito del álgebra y su función principal es agilizar la resolución de un determinado polinomio, sin tener que resolver la propia operación completa. A partir de aquí, obtenemos las fórmulas de los productos notables, las cuales las iremos comentando a lo largo del artículo. Y finalmente, podemos aplicar las fórmulas para hacer la completación de cuadrados, la factorización de polinomios o cualquier otro tipo de cálculo.

¿Cómo resolver un producto notable paso a paso?

Para poder resolver identidades notables tienes que seguir un procedimiento muy sencillo, el cual es también muy lógico:

• Identificar el tipo de identidad notable: el primer paso es identificar el tipo de operación: un producto notable o un cociente notable. También tienes que concretar qué tipo de fórmula tendrás que aplicar, aunque esto lo entenderás más adelante, una vez hayamos explicado los diferentes tipos de identidades notables.
• Aplicar la fórmula: una vez sabes qué fórmula tienes que aplicar, entonces es el momento de hacer los cálculos. Según el tipo de identidad, tendrás que resolver operaciones más o menos complejas y en la gran mayoría de las veces, esos cálculos estarán formados por términos que contengan como mínimo una incógnita.
• Simplificar la expresión: por último, cuando obtienes el resultado, tienes que simplificarlo. En este paso, tienes que agrupar los términos semejantes y ordenarlos para formar un polinomio resultante que esté bien estructurado. Cabe destacar que este paso es igual de importante que los demás, ya que de lo contrario, el ejercicio queda inacabado.

Fórmulas de las identidades notables o productos notables principales

A continuación, puedes encontrar todas las fórmulas correspondientes a las identidades notables. Además de la explicación teórica de cada caso, también hay algunos ejemplos de productos notables resueltos, gracias a los cuales entenderás mejor todos los conceptos. Cabe mencionar que en este primer apartado solamente encontrarás las identidades más importantes. Pero, según vayas leyendo este artículo aprenderás a desarrollar productos notables más complejos, como por ejemplo los que están compuestos por trinomios.

Cuadrado de una suma

El primer caso se trata del cuadrado de la suma, el cual es una expresión polinómica muy habitual en el mundo del álgebra. Este se puede encontrar escrito de la siguiente manera: (a + b)², que equivale a: (a + b) · (a + b). Por lo tanto, sabemos que se puede resolver por medio de una multiplicación de polinomios. Pero, gracias a las identidades notables, podemos ahorrar tiempo usando la siguiente fórmula: (a + b)² = a² + 2ab + b². A continuación, te mostramos la demostración de la fórmula que acabamos de ver, de esta manera, podrás entender de dónde sale y cómo se usa:

Como se puede apreciar, hemos hecho la comprobación a partir de la multiplicación de polinomios que hemos comentado previamente. Y podemos afirmar con total seguridad, que si te sabes la fórmula resultante de memoria, entonces haciendo una simple sustitución de valores puedes obtener el resultado con mayor velocidad. Por lo tanto, es un concepto matemático bastante útil. Ahora que ya sabes cómo funciona el cuadrado de una suma, te mostraremos un ejemplo resuelto:

Ejemplo del cuadrado de una suma

Calcula la identidad notable (2x + 4)²:

Básicamente, hemos asociado los valores del binomio a las letras de la fórmula y hemos resuelto: a = 2x y b = 4. Finalmente, después de resolver todos los cálculos, obtenemos el polinomio 4x² + 16x + 16, el cual es equivalente al original. En este ejemplo, hemos obtenido un polinomio desarrollado (en forma estándar) a partir de un polinomio reducido.

Cuadrado de una resta

Otra expresión muy común es el cuadrado de la resta, la cual es muy similar al cuadrado de una suma, sencillamente cambia por un signo. Entonces, la estructura del binomio equivale a: (a – b)², y si lo desplegamos obtenemos: (a – b) · (a – b). Igual que en el anterior caso, este se puede calcular a partir de una multiplicación de polinomios, aunque también tiene una fórmula que facilita la resolución: a² – 2ab +b². A continuación, puedes encontrar la demostración empírica de esta:

Para simplificar la resolución del cuadrado de una diferencia, podemos usar la misma fórmula que usamos para la suma de un cuadrado, pero con el primer signo en negativo. Este mínimo cambio nos permite adaptar la expresión a binomios compuestos por un término positivo y otro negativo, con lo cual nos sirve para restas. Ahora te mostraremos un ejemplo resuelto:

Ejemplo del cuadrado de una resta

Calcula la identidad notable (x – 3)²:

Como puedes ver en la resolución del ejemplo, hemos sustituido los valores de nuestro binomio en la fórmula, a = x y b = 3. Por lo tanto, usando la fórmula que hemos explicado previamente, solamente hemos tenido que hacer la sustitución y algún cálculo muy básico. Esto nos permite ver la facilidad con la que se puede calcular el cuadrado de una diferencia con esta expresión.

Diferencia de cuadrados o suma por diferencia

El tercer caso de productos notables se llama diferencia de cuadrados, este está formado por el producto de un binomio positivo y un binomio negativo. Una expresión de este estilo tiene la siguiente estructura: (a + b) · (a – b), con lo cual si desarrollamos este producto obtenemos la fórmula que nos facilita el cálculo: a² – b². Como se puede ver, es una fórmula muy sencilla, aunque para entenderla bien hay que desarrollar todos los cálculos:

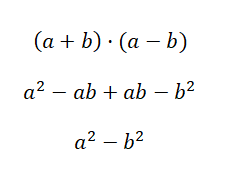
Ejemplo de la suma por diferencia

Calcula la identidad notable (x + 1) · (x – 4):

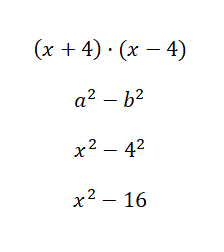
En esta ocasión, el cálculo numérico es muy fácil, de hecho solamente hemos tenido que resolver una potencia. Aunque es cierto, que esta fórmula solo es aplicable cuando los binomios tienen el mismo término principal y el mismo término independiente, pero con signo cambiado. Por lo tanto, esta identidad es importante, pero no es la que más vas a utilizar.

Producto de dos binomios con término común

En este cuarto caso, se nos plantea una situación muy similar a la anterior, aunque con una leve modificación en la estructura. Observa la diferencia que te mostramos: (x + a) · (x + b) y (a + b) · (a – b). Por si aún no la ves muy clara, toma en cuenta el siguiente ejemplo: (x + 4) · (x + 5) y (x + 4) · (x – 4). En el primer caso (el producto de dos binomios con término común) solo hay un único término compartido, mientras que en el segundo caso (la suma por diferencia) los dos términos son comunes, pero el término independiente está cambiado de signo. Dicho esto, vamos a ver con qué fórmula podemos actuar:

Ejemplo del producto de dos binomios con término común

Resuelve el producto notable (x + 2) · (x + 3):

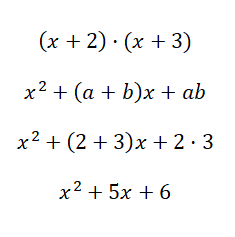
Usando la fórmula de x² + (a + b)x + ab llegamos a calcular el polinomio de segundo grado resultante de la multiplicación de los dos binomios. Esperamos que gracias a este ejemplo hayas entendido la diferencia entre los dos últimos casos que hemos explicado, ya que, a veces puede ser complicado distinguirlos.

Cuadrado de un trinomio

Cuando tratamos de calcular el cuadrado de un trinomio también tenemos un producto notable que nos facilita la vida. Esta expresión se representa así: (a + b + c)² y el producto equivalente es: a² + b² + c² + 2ab + 2ac + 2bc. Cabe destacar que esto es válido en el caso de tener un trinomio positivo, pero si alguno de los coeficientes son negativos, entonces simplemente hay que escribir el valor en negativo dentro de la fórmula. A continuación puedes encontrar la demostración de la fórmula:

Ejemplo del cuadrado de un trinomio

Calcula la identidad notable (2x + 1 + x²)²:

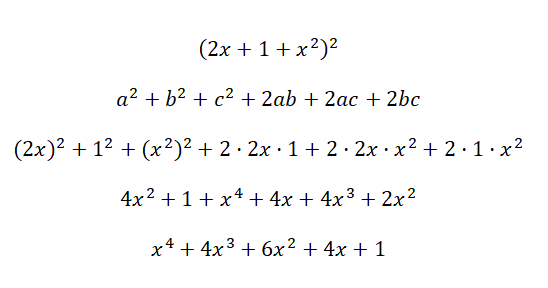
Fórmulas de las identidades notables o productos notables al cubo

Ahora que ya hemos explicado las identidades notables principales, vamos a ver sus derivadas, empezando por los binomios al cubo. Para poder calcular productos notables de este estilo, tendremos que recurrir a unas fórmulas un poco más complejas, pero que siguen una estructura similar a las de los que ya hemos comentado.

Binomio al cubo

El cubo de un binomio se escribe de la siguiente manera: (a + b)³ y (a – b)³, esta expresión es equivalente a la siguiente fórmula: (a³ + 3a²b + 3ab² + b³), y (a³ – 3a²b + 3ab² – b³). Estos dos casos se llaman cubo de una suma y cubo de una resta, ya que son binomios elevados al cubo. A continuación, puedes encontrar una demostración de cada caso muy detalladas:

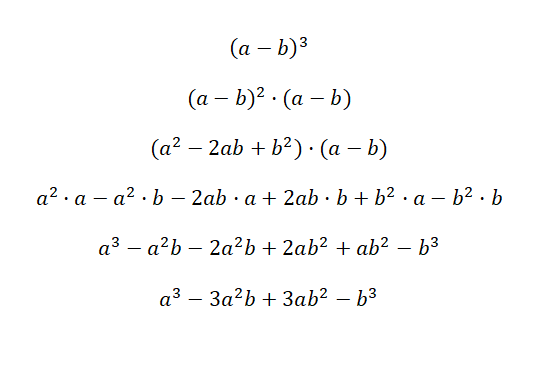
La clave para entender esta primera demostración es entender que (a + b)³ es equivalente a: (a + b)² · (a + b). De esta manera, usamos la fórmula del cuadrado de una suma, que hemos explicado previamente para multiplicar al otro factor. Después, sencillamente simplificamos la expresión, y obtenemos la identidad notable correspondiente: a³ + 3a²b + 3ab² + b³. En el caso del segundo ejemplo pasa lo mismo, pero, con algún cambio de signo.

Ejemplo del cubo de un binomio

Resuelve la identidad notable (x + 3)³:

Empleando la fórmula que acabamos de comentar podemos calcular el polinomio, teniendo en cuenta que: a = x y b = 3. Como puedes ver, el procedimiento es muy fácil y no tiene muchas complicaciones en el cálculo, esto se debe a que tenemos la fórmula. De lo contrario, tener que hacer una multiplicación tan larga como esta sería bastante cansino.

Suma de cubos y diferencia de cubos

También tenemos este otro caso, el cual se puede confundir fácilmente con el anterior. Aunque, ambos casos se escriben de una manera diferente, y no son equivalentes. La expresión equivalente a la suma o diferencia de cubos es: a³ + b³, mientras que en el anterior caso estábamos hablando de: (a + b)³. Como se puede ver, hay una similitud innegable en la estructura de la expresión, pero en realidad, a la hora de desarrollar el cálculo son dos casos totalmente distintos:

En la demostración de la fórmula obtenemos la factorización del primer polinomio, concretamente estamos pasando del binomio inicial al producto de un binomio por un trinomio. Parece que el resultado obtenido (a + b) · (a² – ab + b²), no nos simplifica el cálculo en nada, pero en realidad, al factorizar el polinomio obtenemos una expresión muy fácil de entender.

Ejemplo de la suma de cubos

Calcula el producto notable x³ + 27:

En este caso, el resultado que obtenemos es bastante largo, ya que no se puede simplificar más. Pero, es normal llegar a esta expresión, de hecho, en estos casos solamente puedes obtener un resultado con la estructura equivalente al producto de un binomio por un trinomio, como en este ejemplo.

Trinomio al cubo

El cubo de un trinomio se escribe: (a + b + c)³, lo cual es equivalente a multiplicar tres trinomios idénticos, pero, sin exponente: (a + b + c) · (a + b + c) · (a + b + c). Este es el producto notable más complejo que hay, aunque la fórmula es bastante lógica y se obtiene igual que todas, cuando realizas las multiplicaciones de polinomios correspondientes. A continuación, puedes encontrar la demostración de la fórmula de esta identidad notable:

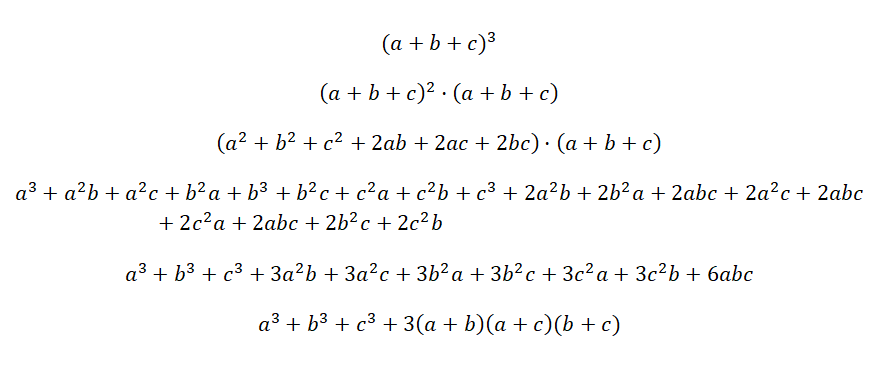
Ejemplo del cubo de un trinomio

Resuelve el cubo de trinomio siguiente (x² + 3x – 4)³:

Cocientes notables

Por último, explicaremos los cocientes notables, los cuales vienen a ser identidades notables que nos permiten resolver rápidamente determinados tipos de fracciones algebraicas. Concretamente, hay cuatro tipos diferentes, los cuales comparten una característica: su resultado está formado por polinomios exactos (con resto igual a cero). También cabe mencionar que las fórmulas de los cocientes notables guardan cierta relación con las fórmulas de los productos notables que ya hemos explicado.

Ejemplo de cocientes notables resueltos

Calcula los cocientes notables siguientes:

Ejercicios de productos notables resueltos

Ahora que ya sabes cómo se resuelven los diferentes productos notables, es hora de que practiques un poco. Es por eso que te proponemos 6 ejercicios para que apliques toda la teoría explicada. Y te mostramos una tabla de las principales identidades notables, para que la tengas a mano mientras resuelves todos los ejercicios:

Ejercicio 1

Resuelve los cuadrados de binomio (x – 4)², (x + 1)² y (x – 3)²:

Ejercicio 2

Calcula las dos diferencias de cuadrados (x – 1) · (x + 1) y (x + 3) · (x – 3):

Ejercicio 3

Desarrolla los productos notables al cubo (x – 5)³ y (x + 8)³:

Ejercicio 4

Desarrolla las identidades notables formadas por términos con varios factores (4x² + 5y)², (5x³ + y²) · (5x³ – y²) y (5xy² – 2xy)²:

Ejercicio 5

Calcula los productos notables al cubo formados por términos con varios factores (3x² + y)³ y (5y³ – 2x²)³:

Ejercicio 6

Resuelve los cuadrados de trinomios (2x² + 3x + 5)² y (3x² + 5x + 6):