En este artículo, repasaremos los conceptos necesarios para comprender qué es un polinomio completo. También, aprenderemos cómo se utiliza y por qué es una idea tan importante para la manipulación y cuantificación de polinomios. Aunque, antes que nada, es muy recomendable que te leas nuestra publicación sobre el polinomio.
Contenido
¿Qué es un polinomio completo?
Un polinomio completo es una expresión algebraica que consta de una suma de términos. Cada término está formado por la multiplicación de un número, llamado coeficiente, por una potencia de x. La potencia más alta en el polinomio se denomina grado del polinomio y la más baja (x elevado a cero) se llama término independiente.
A partir de esto, definimos un polinomio completo como aquel que incluye términos de todos los grados posibles hasta el grado del polinomio. En otras palabras, si un polinomio tiene un grado de 5, entonces debe incluir términos de grado 5, 4, 3, 2, 1 y 0. Dicho de otra manera, un polinomio completo es aquel que no tiene ningún término nulo (igual a cero).
En la imagen siguiente, puedes visualizar un ejemplo de esto. Tal como se puede apreciar, tiene un término para cada exponente de x, desde x elevado a la cuatro (siendo cuatro el grado del polinomio) hasta x elevado a la cero, en el término independiente. Con lo cual, este polinomio cumple con la definición de polinomio completo.
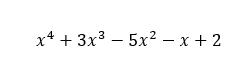
En cambio, si tenemos otro polinomio tal como el de la próxima imagen, estaremos tratando con un polinomio incompleto. Puesto que le faltan dos términos, el de x elevado a la dos y el término independiente. Y partiendo de la definición de polinomio completo, si falta aunque sea un solo término, el polinomio deja de ser completo.
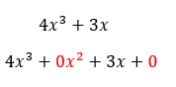
Ejemplos de polinomios completos
Ahora que ya conoces la definición del polinomio completo, vamos a ver algunos ejemplos reales. Empezaremos por ver un polinomio completo de grado 2, otro de grado 4 y por último, uno de grado 6. Evidentemente, podríamos plantear ejemplos de grados mucho mayores, pero la idea es la misma con todos los tipos de polinomios.
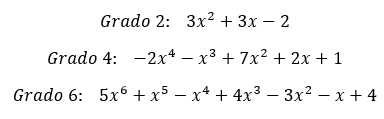
Con estos ejemplos queda muy clara la definición de polinomios completos. Es por eso que ahora ya podemos pasar al siguiente nivel. En el próximo apartado te detallaremos los dos tipos de polinomios completos que existen, según el orden de los términos. Es algo que muchos estudiantes dan por entendido, pero es bueno repasarlo.
Tipos de polinomios completos
Podemos clasificar los polinomios completos en dos tipos: polinomios completos ordenados y polinomios completos no ordenados o desordenados. Los primeros se caracterizan por tener una estructura que tiene los términos ordenados según los grados de la x. Empezando por el grado mayor y acabando por el término independiente.
Mientras que un polinomio completo desordenado, está expresado con los términos en un orden aleatorio. Por lo tanto, puedes encontrarte el término con mayor exponente al lado del término independiente. Pero, esta forma de expresar un polinomio es poco práctica, por eso te recomendamos que uses siempre los polinomios ordenados.
A continuación, te mostraremos un ejemplo de cada tipo, para que puedas apreciar bien la diferencia.
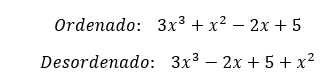
Esperamos que este artículo te haya ayudado a entender el concepto de polinomios completos. Si tienes cualquier pregunta, no dudes en dejarla en los comentarios.