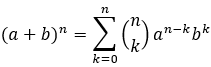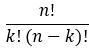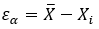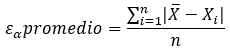La regresión lineal es un método estadístico que se utiliza para estudiar la relación entre dos variables continuas. La idea principal de la regresión lineal es encontrar la línea recta que mejor se ajuste a los datos. Además, que permita predecir el valor de una variable en función del valor de otra.
Esta línea recta se llama “regresión” y se utiliza para predecir valores desconocidos o para entender la relación entre las variables. En resumen, la regresión lineal es una herramienta para analizar y modelar la relación entre dos variables continuas.
¿Por qué es importante la regresión lineal?
La regresión lineal es importante porque permite modelar y analizar la relación entre dos variables continuas, lo que puede ser útil en la predicción de valores futuros y en la identificación de patrones y tendencias en los datos.
Además, la regresión lineal es una herramienta fundamental en la estadística y en la mayoría de las áreas de la investigación científica y social, incluyendo la economía, la psicología, la medicina, la ingeniería y la física, entre otras. También se utiliza en la toma de decisiones empresariales y en la optimización de procesos en la industria y los negocios.
En resumen, la regresión lineal es una herramienta poderosa y versátil que permite analizar y comprender mejor los datos y las relaciones entre variables en diversos campos de la investigación y la práctica.
¿Cuáles son los tipos de regresión lineal?
Existen varios tipos de regresión lineal, algunos de los cuales son:
Regresión lineal simple
El análisis de regresión lineal simple es una herramienta muy utilizada para estudiar el efecto de una variable independiente sobre una única variable dependiente, en la que se considera que existe una relación lineal entre ellas. La ecuación de la regresión lineal simple permite estimar los valores de la variable dependiente en función de los valores de la variable independiente.
La fórmula de la regresión lineal simple es:
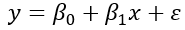
Donde, β0 es el valor de la variable dependiente cuando la variable independiente es igual a cero. β1 representa el cambio en la variable dependiente por unidad de cambio en la variable independiente y ε representa el residuo o error. Es decir, la variabilidad de los datos que no puede explicarse mediante la relación lineal de la fórmula.
Regresión lineal múltiple
La regresión lineal múltiple es utilizada cuando se tienen más de una variable independiente que puede afectar a la variable dependiente que se está estudiando.
La fórmula de la regresión lineal múltiple es:

Donde, Y representa la variable dependiente, β1, β2, βn son las variables independientes que pueden afectar al valor de Y, X1, X2, Xn son los valores de las variables independientes, 0 es la intersección de la línea de regresión y ε representa el posible error existente. Esta fórmula nos permite estimar el valor de Y en función de los valores de las variables independientes.
¿Cuál es la fórmula de regresión lineal?
La fórmula de regresión lineal es:

Donde:
y es la variable dependiente (o respuesta) que se quiere predecir
x es la variable independiente (o predictora) que se utiliza para hacer la predicción
a es la ordenada al origen (o el punto donde la línea de regresión corta el eje Y cuando x=0)
b es la pendiente de la línea de regresión (que indica la tasa de cambio en y para cada cambio en x)
Para encontrar los valores de a y b, se utiliza el método de mínimos cuadrados, que busca minimizar la suma de los errores cuadráticos entre los valores observados y los valores predichos por la línea de regresión.
A continuación, te proporcionamos las fórmulas:
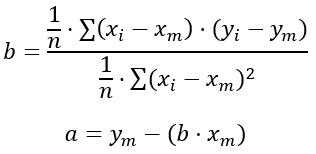
Donde:
n es el total de grupos de datos que tenemos.
xi e yi son los valores que tomamos en el sumatorio.
xm e ym son los valores medios de cada variable.
¿Cómo aplicar el método de regresión lineal?
El método de regresión lineal se puede aplicar siguiendo los siguientes pasos:
- Recolectar datos: lo primero que se debe hacer es recolectar los datos de interés. Por ejemplo, si se quiere estudiar la relación entre el salario y la edad de un grupo de personas, se debe recolectar información sobre el salario y la edad de cada una de ellas.
- Graficar los datos: luego, se debe graficar los datos en un plano cartesiano, donde la variable independiente (en este caso, la edad) se coloca en el eje horizontal y la variable dependiente (el salario) se coloca en el eje vertical.
- Determinar la línea de regresión: se debe determinar la línea de regresión que mejor se ajuste a los datos. Esta línea se obtiene a partir de la fórmula de regresión lineal, la cual se calcula utilizando los datos de la muestra estadística.
- Evaluar la calidad del ajuste: es importante evaluar la calidad del ajuste de la línea de regresión a los datos. Esto se puede hacer utilizando medidas estadísticas.
- Realizar predicciones: finalmente, se pueden realizar predicciones utilizando la línea de regresión obtenida. Por ejemplo, si se quiere predecir el salario de una persona de 30 años, se debe utilizar la fórmula de regresión lineal y sustituir el valor de la edad en la misma.
Es importante destacar que estos pasos pueden variar ligeramente dependiendo del tipo de regresión lineal que se esté utilizando y del software estadístico que se esté empleando.
¿Para que sirve la regresión lineal?
La regresión lineal se utiliza cuando se quiere analizar la relación entre dos variables, en donde una variable puede afectar el valor de otra variable. Por lo tanto, se puede utilizar la regresión lineal para entender cómo una variable independiente afecta a una variable dependiente, y para predecir el valor de la variable dependiente en función de la variable independiente.
Es importante tener en cuenta que la regresión lineal asume que la relación entre las dos variables es lineal, lo que significa que el cambio en la variable dependiente es proporcional al cambio en la variable independiente.
Por lo tanto, la regresión lineal se debe utilizar cuando se sospecha que existe una relación lineal entre las dos variables. Si no se cumple esta condición, puede que sea más adecuado utilizar otros modelos de regresión no lineal o métodos estadísticos diferentes.
¿Cuáles son las aplicaciones de la regresión lineal?
La regresión lineal se utiliza en una amplia variedad de aplicaciones en campos como la estadística, la economía, la ingeniería, la ciencia social, la biología, entre otros. A continuación, se presentan algunas de las aplicaciones más comunes de la regresión lineal:
- Análisis de tendencias: para analizar tendencias en datos históricos y predecir tendencias futuras.
- Pronósticos: predecir el valor futuro de una variable en función de los valores pasados de una o más variables.
- Investigación de mercados: estudiar la relación entre la demanda de un producto y su precio.
- Análisis financiero: estudiar la relación entre los ingresos y los gastos de una empresa y predecir los resultados financieros futuros.
- Estudios epidemiológicos: estudiar la relación entre la exposición a un factor de riesgo y la probabilidad de desarrollar una enfermedad.
- Ciencias sociales: estudiar la relación entre dos o más variables en campos como la psicología, la sociología y la ciencia política.
- Investigación de operaciones: la regresión lineal se utiliza para modelar y optimizar sistemas complejos en campos como la ingeniería industrial y la logística.
- Ciencias ambientales: se utiliza para estudiar la relación entre los factores ambientales y los efectos en los ecosistemas.
¿Qué son los residuos en la regresión lineal?
Los residuos en la regresión lineal son la diferencia entre los valores observados de la variable dependiente y los valores predichos por el modelo de regresión lineal. En otras palabras, son la distancia vertical entre los puntos de datos reales y la línea de regresión.
La idea detrás de los residuos es que, si la línea de regresión se ajusta bien a los datos, los residuos deberían ser pequeños y aleatorios. Si los residuos son grandes o siguen algún patrón, puede ser una señal de que la relación entre las variables no es lineal o que el modelo de regresión lineal no es adecuado para los datos.
Los residuos también se utilizan para evaluar la precisión del modelo de regresión lineal y para identificar puntos de datos atípicos o influenciadores que pueden estar afectando la calidad del modelo.
¿Puedo realizar una regresión lineal con más de una variable dependiente?
En la regresión lineal, la variable dependiente es siempre una única variable. Sin embargo, se puede tener más de una variable independiente. En este caso, se estaría hablando de regresión lineal múltiple.
En la regresión lineal múltiple, se trata de estudiar el efecto de varias variables independientes sobre una única variable dependiente.
¿Cómo puedo interpretar los coeficientes en la regresión lineal?
En la regresión lineal, los coeficientes representan la pendiente y la intersección de la línea de regresión. La pendiente indica el cambio en la variable dependiente por unidad de cambio en la variable independiente, mientras que la intersección representa el valor de la variable dependiente cuando la variable independiente es igual a cero.
Ejemplos numéricos de regresión lineal
Un ejemplo sencillo puede ser el siguiente:
Supongamos que tenemos los siguientes datos de edad y altura de un grupo de personas:
| Edad (años) | Altura (cm) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| 45 | 190 |
Queremos determinar si existe una relación entre la edad y la altura de estas personas. Para ello, utilizaremos la regresión lineal.
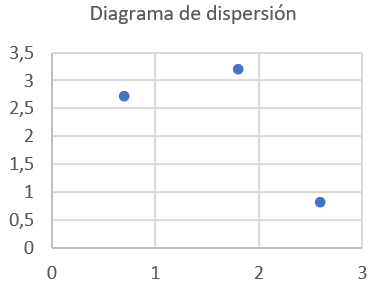
Primero, podemos dibujar un gráfico estadístico con los datos (en este caso recomendamos usar un diagrama de dispersión):
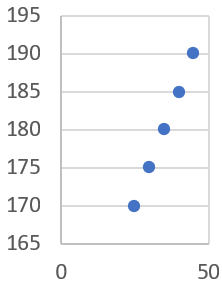
Podemos observar que hay una clara tendencia a que a medida que la edad aumenta, también lo hace la altura. Podemos confirmar esto calculando la recta de regresión lineal.
Calculando los coeficientes de la recta de regresión lineal con las fórmulas que hemos visto antes, obtenemos:
a = 145
b = 1
Por lo tanto, la ecuación de la recta de regresión lineal es:
Altura = 145 + 1 · Edad
Podemos utilizar esta ecuación para predecir la altura de una persona en función de su edad. Por ejemplo, si una persona tiene 32 años, podemos predecir que su altura sería de:
Altura = 145 + 1 · 32 = 177 cm