Calculadoras online

Una regla de tres nos permite conocer las relaciones de proporcionalidad que existen entre unos valores determinados. Es gracias a esto que lo aplicamos casi a diario en cualquier ámbito de la vida cotidiana. Por poner algún ejemplo: calcular porcentajes, hacer conversiones entre unidades (de masa, volumen, tiempo…) y en general hacer cálculos a partir de equivalencias. Esta última aplicación es la que nos permite usar este recurso matemático en casi cualquier temática.

Entonces si quieres aprender a resolver reglas de tres, te recomendamos que te quedes hasta el final del artículo. En el cual explicaremos cómo resolverlas, qué tipos hay, sus aplicaciones y hasta encontrarás algunos ejemplos resueltos. En resumen, para cuando termines de leer este artículo sabrás todo lo que hay que saber sobre este concepto matemático.

Calculadora de regla de tres

Con la ayuda de estas calculadoras de reglas de tres (la primera es de proporcionalidad directa y la segunda es de proporcionalidad indirecta), podrás comprobar y corregir todos tus ejercicios. Su funcionamiento es muy sencillo, simplemente deberás introducir los datos que conoces en tres de las cuatro casillas y cuando pulses en el botón de calcular se mostrará el valor de x. Pero no te preocupes si aún no sabes cómo estructurar un cálculo de este tipo, porque en el siguiente apartado te lo explicaremos detalladamente.

Calculadora de regla de tres directa

   ───   

   ───   



Resultado:

Calculadora de regla de tres inversa

   ───   

   ───   



Resultado:

¿Cómo se hace una regla de tres?

Para resolver una regla de tres, antes deberemos identificar cuál usaremos: regla de tres directa o regla de tres indirecta. También deberemos distinguir entre qué tipo de proporcionalidad usaremos: regla de tres simple o regla de tres compuesta. Ya que cada una tiene una de estas opciones tiene una forma de organizar los datos y una fórmula distinta. Entonces para saber cuándo elegir cada uno de los tipos, te recomendamos que te leas la siguiente explicación sobre el procedimiento de la resolución de una regla de tres.

1. Identificar las relaciones entre las diferentes variables

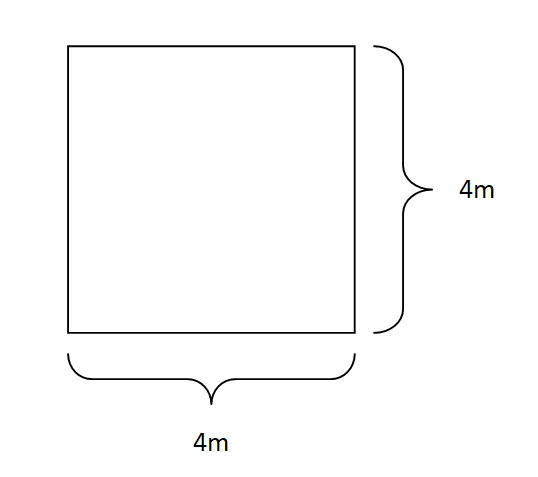
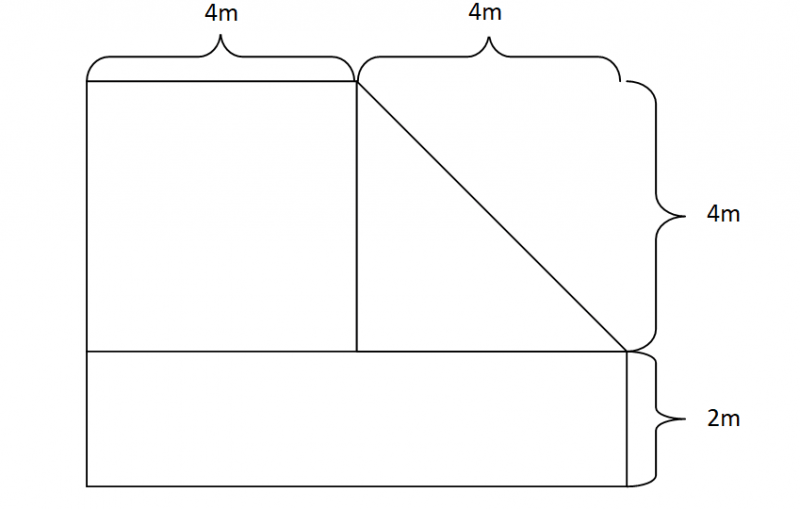
El primer paso a seguir para resolver una regla de tres es hacer una especie de esquema o relación entre las variables. Por lo general, se suele hacer con el típico diagrama que se puede apreciar en la imagen de abajo. Gracias a esto tendremos más clara la estructura del cálculo y posteriormente, podremos realizar los cálculos. Simplemente deberás sustituir las letras A, B y C con los valores correspondientes: a la columna de la izquierda irán los valores numéricos de la magnitud que conoces entera (ambos valores) y a la columna de la derecha irán los valores de la magnitud que tiene la incógnita. También deberás respetar las filas, por lo tanto la A deberá ser el valor de la magnitud de la izquierda que se relacione con la variable B.

2. Establecer la proporcionalidad de una regla de tres

El siguiente paso será identificar la proporcionalidad que hay entre las variables, esto lo haremos analizando el cambio del valor numérico entre las variables de cada magnitud. Si nos encontramos con una regla de tres directa, entonces cuando una de las magnitudes aumente la otra también lo hará. Pero si nos encontramos con una regla de tres inversa, cuando una de las magnitudes aumente la otra disminuirá. Es importante tener esto en cuenta, porque la fórmula variará según el caso.

3. Reglas de tres simples o compuestas

Por último diferenciaremos en dos tipos las reglas de tres, según la cantidad de variables que relacionamos por medio de la proporcionalidad. En el caso de la regla de tres simple, obtenemos el valor de la variable X a partir de la proporcionalidad de otra magnitud. Mientras que la regla de tres compuesta nos permite calcular la variable X, partiendo de la proporcionalidad de dos o más magnitudes. A continuación te mostraremos las fórmulas y la representación gráfica de estos dos conceptos, para que no queden dudas al respecto:

Ejemplo de una regla de tres simple

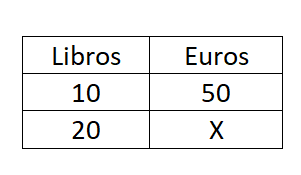
Si diez libros cuestan cincuenta euros, entonces si compramos 20 libros ¿cuánto dinero gastaremos?

Para obtener el resultado deberemos resolver una regla de tres simple y directa. Por lo tanto, usaremos la fórmula X = (B · C) / A: X = (50 · 20) / 10 = 100 €.

Ejemplo de una regla de tres compuesta

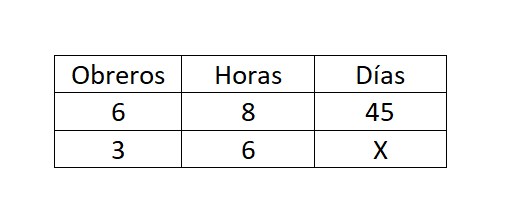
Si 6 obreros trabajando 8 horas diarias, construyen una casa en 45 días, ¿cuántos días tardarán 3 obreros trabajando 6 horars diarias en hacer la misma construcción?

En este caso tenemos una regla de tres compuesta e indirecta. Por lo tanto, usaremos la fórmula X = (A₁ · B₁ · C₁) / (A₂ · B₂): X = (6 · 8 · 45) / (3 · 6) = 120 días.

Aplicaciones de la regla de tres

Como hemos comentado en la introducción, las reglas de tres nos permiten calcular muchísimas cosas y, por lo tanto, las aplicamos en cualquier ámbito de la vida cotidiana. Aunque este tipo de aplicaciones, tiene una característica común y es que se calcula por medio de proporciones. Por poner unos ejemplos:

• Cálculo de porcentajes
• Conversiones entre unidades
• Calcular dosis de medicamentos
• Calcular comisiones
• Calcular calificaciones

Y en realidad, casi cualquier operación que requiera de una equivalencia o similar.

Regla de tres en la calculadora científica

En las calculadoras científicas más comunes no suele haber ninguna función, ni tecla que nos permita resolver reglas de tres. Entonces si no cuentas con una calculadora avanzada, en la cual puedas añadir funcionalidades personalizadas, difícilmente vas a poder resolver reglas de 3. Por lo tanto, deberás hacer el planteamiento aparte (en una hoja o en tu cabeza) y luego realizar la parte de cálculo en la calculadora. Al principio puede parecer un poco lento, pero cuando coges práctica y eres capaz de imaginar la regla de tres dibujada en tu mente, entonces podrás resolverlas en un segundo.

Por último comentarte que si quieres más ejercicios de reglas de tres para repasar, te dejamos un enlace con ejercicios para que practiques. Dicho esto, esperamos que este artículo y nuestra calculadora de regla de 3 online te hayan ayudado a entender mejor este concepto matemático.

¿Qué es la media aritmética y cómo se calcula? La media es un valor numérico que se obtiene al sumar un conjunto de números establecido y dividir el resultado entre el número de valores. Por ejemplo, si queremos calcular la media aritmética de los datos 2, 4, 1 y 6, entonces deberemos hacer el siguiente cálculo: (2 + 4 + 1 + 5) / 4 = 3. A continuación en este artículo te explicaremos en mayor profundidad cómo averiguar el promedio de un conjunto de números. Además, tendrás a tu disposición la siguiente calculadora de media aritmética, para que puedas comprobar si tus resultados son correctos.

Calculadora de promedio online

Si quieres calcular el promedio de una serie de números puedes usar esta calculadora de media aritmética online, gracias a la cual podrás comprobar los resultados de tus ejercicios y saber si los has resuelto correctamente. Su uso es muy simple, ya que solamente deberás introducir los números que componen el conjunto (separados por comas) y seguidamente deberás pulsar en el botón de calcular. Recuerda introducir los números decimales con un punto (no una coma).

Calcular

¿Cómo calcular la media aritmética?

Existe una fórmula de la media aritmética que nos permite calcularla basándose en cualquier serie o conjunto de números:

Por ejemplo, si quieres calcular el promedio de un conjunto de números [1, 4, 7, 2, 5, 10], solamente deberás sumarlos y dividir ese resultado entre el número de valores que hayas sumado previamente: (1 + 4 + 7 + 3 + 5 + 10) / 6 = 5. Aunque a veces tendremos que calcular la media aritmética de los valores de una tabla de frecuencias. En estos casos deberemos aplicar la misma fórmula, pero multiplicando cada número por las veces que salga (su frecuencia absoluta) e igualando N a la suma de frecuencias absolutas. Por ejemplo, (1 x 4 + 3 x 2 + 5 x 4) / (4 + 2 + 4) = 3.

También podemos expresar esta fórmula como el sumatorio de N con base i (Σ_i^N) y luego dividido entre N. Esta última expresión es otra forma de decir lo mismo que en la imagen de arriba. Aunque esta se suele encontrar más en los libros de texto de matemáticas, por eso es importante conocerla.

Propiedades de la media aritmética

• Suma de desviaciones: la suma de las desviaciones de todos los datos respecto a la media del conjunto es igual a cero, a partir de esta propiedad podemos deducir la siguiente fórmula Σ(X_i - x̄) = 0.
• Suma de cuadrados de las desviaciones: cuando sumas los cuadrados de las desviaciones de todos los datos respecto a la media aritmética, obtenemos un valor numérico mínimo. Entonces Σ(X_i - x̄)² ≤ Σ(X_i - a)², a ∈ ℝ.
• Media aritmética equivalente: si sumamos un valor x a todos los valores que conforman el conjunto numérico, entonces el promedio de esos números equivaldrá a la suma de la anterior media aritmética y el número que se haya añadido: x̄ = x̄₀+a. Esto también pasa en el caso del producto.

Aplicaciones del promedio

Por lo general, usamos este recurso matemático para calcular un valor representativo de nuestro conjunto, con el cual podamos entender de manera simplificada el comportamiento del grupo numérico. Un ejemplo sería para calcular la nota media de la clase, de esta manera podremos conocer una puntuación orientativa del total de alumnos. También solemos usar la media en los experimentos científicos, ya que muchas veces deberemos recoger varios resultados y hacer la media para tener uno más preciso.

Ejercicios resueltos de la media aritmética

A continuación te plantearemos unos ejercicios sobre los tres principales tipos de media aritmética, recuerda que todos se resuelven con los métodos explicados en este artículo. Y si quieres puedes realizar la parte numérica (cálculos) con la calculadora que hay más arriba y con nuestra calculadora online. Dicho esto, te dejamos practicar:

Media aritmética básica

Calcula la media aritmética del conjunto de datos siguiente [2, 5, 3, 7, 6, 1]. Una vez lo hayas hecho, deberás calcular el promedio del mismo grupo de números, pero multiplicados todos por 2:

Para resolver el primer apartado simplemente deberemos utilizar la fórmula que hemos comentado un poco más arriba: x̄ = (2 + 5 + 3 + 7 + 6 + 1) / 6 = 4. Y para calcular la media en el segundo apartado, deberemos hacer el mismo cálculo pero multiplicando cada número por 2: (2 x 2 + 5 x 2 + 3 x 2 + 7 x 2 + 6 x 2 + 1 x 2) / 6 = 8. Como podemos ver, el resultado de la media es el doble en el segundo caso, lo cual era predecible porque se cumple la propiedad del producto equivalente.

Media aritmética para datos agrupados

Las notas de matemáticas de quince estudiantes son: 5, 8, 7, 4, 9, 3, 6, 8, 7, 8, 9, 7, 5, 8, 8. Calcula la media de la clase:

En este caso deberemos contar cuántas veces aparece cada número en la lista y luego resolveremos el cálculo con la fórmula de la media aritmética aplicada a datos agrupados (fórmula en la que interviene la frecuencia absoluta): x̄ = (3 x 1 + 4 x 1 + 5 x 2 + 6 x 1 + 7 x 3 + 8 x 5 + 9 x 2) / 15 = 6,8. A modo de conclusión podemos ver que pese a haber bastantes notas altas, los valores bajos afectan muy negativamente a la media global.

Cálculo a partir de una media conocida

Si sabemos que la media de dos números es igual a 9,25 y uno de los dos números es 6, ¿cuál será el segundo número?

Para calcular el segundo valor deberemos montar una ecuación a partir de la fórmula que hemos estado usando todo el rato en los ejercicios: (6 + x) / 2 = 9,25. Finalmente aislaremos x y obtendremos su valor numérico, el cual equivale al del segundo número. En este caso x = 12,5.

El mínimo común múltiplo (mcm) de dos o más números es el múltiplo más pequeño (diferente a cero) que tienen en común esos números. Esto viene a ser la operación contraria del máximo común divisor, aunque se calcula por medio de métodos similares. Si quieres aprender a calcular el mcm te recomendamos que sigas leyendo, porque en este artículo te explicaremos todos los procedimientos (desde los más fáciles hasta los más complicados) para sacar el mínimo común múltiplo de un conjunto de números.

Calculadora de mcm

Antes de empezar a hablar sobre cómo obtener el mcm, queremos que sepas que en esta página disponemos de una calculadora de mínimo común múltiplo. Con ella conseguirás calcular el mcm de todos los números que quieras, de esta manera podrás comparar los resultados de tus ejercicios para ver si los has resuelto bien.

Para usar la calculadora de mínimo común múltiplo, introduce los números enteros separados por una coma:

Calcular mcm

¿Cómo calcular el mínimo común múltiplo?

Para hallar el mínimo común múltiplo de dos o más números deberás seguir alguno de los tres métodos que te explicaremos a continuación. A continuación, cuando entremos en más detalle sobre cada uno de los procedimientos que puedes elegir, también te diremos cuáles son sus ventajas y sus desventajas. Así sabrás cuál elegir en cada situación para resolver de manera fácil y rápida el mcm en cuestión.

Método 1: Listado de múltiplos

El primer método consiste en crear una lista de los múltiplos de los números que quieres calcular en el mcm. Entonces, deberás buscar el valor más pequeño que se repita en todos los listados, de esta manera tendrás el mínimo común múltiplo. A continuación lo veremos con un ejemplo: mcm (5, 6).

Método 2: Descomposición factorial

En segundo lugar, podemos optar por descomponer factorialmente los números. Concretamente este método nos facilitará el cálculo del mcm de números grandes. Ya que seguir el método 1 a la hora de hacer el mcm de números grandes puede ser lento y pesado, sencillamente porque deberemos escribir unas listas de múltiplos muy largas. Este segundo procedimiento puede ser un poco más complicado de entender al principio, pero cuando entiendes la mecánica presenta muchas ventajas respecto al anterior. Dicho esto, veamos el procedimiento a seguir:

• Descomposición factorial: el primer paso será descomponer en factores primos todos los números que vayamos a incluir en el mcm. En el caso de que no sepas descomponer factorialmente un número, te recomendamos que entres a este último link, allí encontrarás una explicación de primera sobre cómo simplificar números de manera rápida y eficaz.
• Crear una única expresión matemática: cuando tengamos todos los números expresados en factores primos, elegiremos los comunes y no comunes elevados al mayor exponente. Seguidamente, los escribirás en una sola expresión matemática y finalmente resolverás las multiplicaciones y/o potencias necesarias. Y ya tendrás el valor numérico del mcm.

Método 3: Fórmula matemática

Existe un último camino para obtener el mínimo común múltiplo que es por medio del MCD y la fórmula matemática siguiente:

Mediante esta fórmula podremos calcular el mcm de cualquier número. Vamos a ver un ejemplo real, si queremos calcular el mcm (2,6) sencillamente deberemos resolver la operación (2 x 6) / 2 = 6. Y ya habremos resuelto el cálculo, como se puede ver es un método sencillo y rápido si dispones del MCD o puedes calcularlo fácilmente.

Trucos calcular el mcm rápidamente

Cuando domines los tres métodos que acabamos de explicar, te recomendamos que leas las propiedades del mínimo común múltiplo que comentaremos ahora. Ya que gracias a ellas podrás identificar algunas situaciones concretas en las cuales se puede calcular el mcm muy rápidamente, sin tener que usar las estrategias ya explicadas.

• Primer número divisible entre el segundo: si queremos calcular el mínimo común múltiplo de a y b cuando a divide b, entonces el mcm de estos dos números será el mayor (en este caso b). Por ejemplo, si quieres calcular el mcm de 2 y 8, el resultado va a ser el mayor, por lo tanto, el 8.
• Dos números primos: en el caso de encontrarnos con dos números primos, el método más rápido es multiplicarlos entre sí y el resultado será el mcm. Esto es lógico, ya que su máximo común divisor es 1, lo cual quiere decir que no podremos descomponer el número en factores más simples que el mismo número y, como resultado, solamente podremos multiplicarlos entre ellos. Por ejemplo, el mcm de 3 y 5 será el resultado de su producto: 3 x 5 = 15.

Vídeo explicativo del mínimo común múltiplo

¿Cómo sacar el mínimo común múltiplo en fracciones?

Cuando queremos resolver una suma o resta de fracciones necesitamos calcular el mínimo común denominador, que viene a ser lo mismo que el mcm, pero aplicado a las fracciones. Básicamente, buscamos el mcm de los dos denominadores para después poder expresar la suma en una sola fracción. Si quieres ver cómo se aplica el mínimo común denominador a un cálculo de fracciones real, puedes entrar en este enlace.

Mcm en la calculadora científica

La tecla MCM, que se puede encontrar en cualquier calculadora científica, permite calcular el mínimo común múltiplo de dos números enteros. En el caso de las calculadoras Casio la sintaxis o el procedimiento que debes seguir es el siguiente. Primero de todo, pulsas APHA + MCM (esta última tecla estará etiquetada de color granate). Una vez lo hayas hecho, podrás introducir los dos números, pero recuerda que deberás separarlos por una coma (SHIFT + ,). Finalmente, obtendrás el mínimo común múltiplo pulsando en el botón de igual.

Ejercicios de mcm resueltos paso a paso

A continuación te mostraremos tres ejemplos del mínimo común múltiplo resueltos paso a paso. De esta manera, podrás probar de resolver estos problemas y practicar un poco lo que hemos explicado en este artículo. Es importante que intentes resolver los ejercicios si quieres interiorizar los conceptos, puesto que es necesario aplicar la teoría a la realidad. Dicho esto, te dejamos practicar con los ejercicios:

Calcular el mcm de 4 y 6

Calcular el mcm de 6 y 9

Calcular el mcm de 30 y 40

A la hora de hacer deporte es importante conocer las capacidades de nuestro cuerpo, de esta manera conseguiremos entrenar más eficientemente. Por eso es de vital importancia conocer tu frecuencia cardíaca máxima, que viene a ser las pulsaciones máximas por minuto que puede alcanzar tu corazón sometido al máximo esfuerzo. Entonces, en este artículo te comentaremos cuáles son los distintos métodos que existen para calcular la frecuencia cardíaca máxima y cómo aplicarlo a tus entrenos.

¿Cómo calcular la frecuencia cardíaca máxima?

Podemos obtener el valor numérico de la FCmax por medio de varios métodos, algunos son más rápidos y fáciles que otros, pero pueden ser más inexactos. Nosotros te recomendamos probar varios procedimientos si quieres conocer de la manera más exacta posible tu FCmax. Por otro lado, si quieres conocer un valor aproximado con la primera opción te valdrá.

Calculadora de frecuencia cardíaca máxima

Esta calculadora de FCmax está basada en la fórmula de 220 – edad, esto quiere decir que ofrece un valor orientativo. Por lo cual, el resultado que te dará esta calculadora deberás pensarlo con una variación de ± 20 latidos por minutos. Aunque si quieres conocer el valor real de tu frecuencia cardíaca máxima, entonces te recomendamos que vayas al siguiente apartado. Ya que como hemos dicho, este solamente te ofrecerá un resultado universal.

Edad:

FCmax: pulsaciones

Fórmula de la frecuencia cardíaca máxima exacta

A continuación puedes encontrar un listado con las tres fórmulas para calcular la FCmax según el sexo y el estado físico. Recuerda que todas tienen en cuenta las mismas variables, pero cada una tiene un número de pulsaciones y un coeficiente de variación según la edad distintos.

• Personas no entrenadas: 220 – edad
• Atletas masculinos: 209 – (0,7 x edad)
• Atletas femeninas: 214 – (0,8 x edad)

Calcular la fc máxima haciendo deporte

El último método que comentaremos para calcular la frecuencia cardíaca máxima de una persona es mediante una prueba física. Se trata de un ejercicio físico que nos servirá como test para saber la FCmax. Si eres un atleta profesional te recomendamos que hables con tu médico o entrenador para saber qué tipo de ejercicio hacer. Y si eres alguien poco entrenado también te recomendamos que hables con tu médico antes de hacer la prueba, para saber si estás capacitado. Dicho esto, a continuación te mostraremos un modelo de entrenamiento que puedes seguir.

• Calentamiento: trata de calentar durante aproximadamente unos 15 minutos para subir un poco la intensidad hasta alcanzar tu nivel de entrenamiento habitual. De esta manera, te prepararás para hacer un ejercicio a la máxima intensidad que puedas de manera segura y saludable.
• Primera parte: después deberás buscar un terreno que tenga una cierta inclinación y que requiera varios minutos para subir hasta arriba del todo. Entonces, deberás subirlo en dos minutos con una velocidad que puedas aguantar durante veinte minutos y seguidamente volver hasta abajo del todo.
• Segunda parte: cuando llegues a la base del pendiente deberás volver a subirlo, pero esta vez con un ritmo que solamente puedas aguantar tres kilómetros. Mientras lo hagas ve midiendo tus pulsaciones con un reloj inteligente o alguna herramienta de este estilo. Luego deberás bajarlo tranquilamente otra vez disminuyendo las pulsaciones en unas 30 o 40.
• Subida definitiva: finalmente deberás subir el pendiente en un minuto intentando llegar hasta la mitad de la distancia que recorrías antes. Es en este momento que deberás fijarte en tu FC porque los valores que verás por la pantalla serán muy próximos a tu FC real.

¿Qué son y cómo calcular las zonas de frecuencia cardíaca?

Podemos dividir nuestro esfuerzo físico en cinco categorías diferentes, las cuales se calculan a partir de las pulsaciones por minuto. Ya que estas son un gran indicador de la intensidad de un ejercicio físico. Además, establecer esta escala de intensidades nos permite estructurar mejor un entrenamiento físico, tanto para atletas profesionales como para gente que está empezando a hacer un poco de deporte.

• Zona de frecuencia cardíaca 1: esta fase es de una intensidad muy ligera (50%-60%) y se suele planificar en una pauta de entrenamiento para volver a la calma y recuperarte de un entrenamiento exigente. Podrías estar en esta fase durante horas, ya que resulta muy fácil.
• Zona de frecuencia cardíaca 2: en este segundo nivel nos encontramos con una intensidad ligera (60%-70%), la cual continúa siendo cómoda. Suele ser el segundo paso del entrenamiento y nos hace quemar grasa, porque permite al cuerpo utilizar la grasa como fuente de energía.
• Zona de frecuencia cardíaca 3: al fin llegamos al tercer nivel el cual alcanza una intensidad moderada (70%-80%), la cual te hace mejorar tu forma aeróbica. Es a partir de aquí que empezarás a respirar más fuerte, porque estarás trabajando la eficiencia del corazón y la mejorarás tu rendimiento físico.
• Zona de frecuencia cardíaca 4: cuando llegamos a un nivel de esfuerzo intenso (80%-90%) empezamos a trabajar la resistencia en velocidad y nuestra capacidad para soportar una mayor acumulación de lactato en la sangre. El objetivo de este entrenamiento es mejorar el rendimiento en el deporte y no la condición física.
• Zona de frecuencia cardíaca 5: finalmente cuando entrenamos a un nivel de esfuerzo muy intenso (90%-100%) estamos trabajando al nivel máximo que nuestros órganos y músculos pueden soportar. Aquí de nuevo se busca mejorar el rendimiento para deportistas profesionales, ya que no podrás aguantar mucho tiempo en esta zona.

Frecuencia cardíaca de trabajo ideal

Para calcular la frecuencia cardíaca de entreno ideal para ti, te recomendamos usar la fórmula de Karvonen, la cual nos permite adaptar el nivel de esfuerzo a cualquier zona de intensidad. Cabe destacar que su exactitud radica en que realiza el cálculo a partir de tus pulsaciones máximas y tus pulsaciones de reposo. Entonces, utiliza valores «personalizados» para cada persona. La expresión matemática es la siguiente: Frecuencia cardíaca de trabajo = (FCmax – FCreposo) x porcentaje intensidad + FCreposo

Por ejemplo, si tienes una frecuencia cardíaca máxima de 185 pulsaciones y una frecuencia de reposo de 50. Digamos que quieres entrenar en la zona moderada, concretamente al 75% de tu capacidad, entonces simplemente deberás resolver la siguiente operación matemática: FCtrabajo = (185 – 50) x 0,75 + 50 = 151 pulsaciones / minuto.

Conclusión sobre la frecuencia cardíaca máxima

Conocer tu frecuencia cardíaca máxima es muy importante para establecer tus objetivos deportivos y diseñar tu plan de entrenamientos. Ya que te permitirá saber con exactitud qué tipo de ejercicios te beneficiarán más y te ayudarán a mejorar tu rendimiento físico. Por último, queremos comentarte que disponemos de un contador de días el cual también te puede ayudar a idear tu plan deportivo. Gracias a esta herramienta puedes establecer los intervalos de días que harás un determinado ejercicio…

El máximo común divisor o MCD es un concepto matemático que nos permite calcular el mayor número que es divisible entre a y b. Esto en el caso de querer calcular el MCD de dos números, aunque en realidad podemos calcular el divisor más grande de un conjunto de números más amplio. Por ejemplo en la calculadora de MCD que te mostramos a continuación podrás escribir todos los valores numéricos que quieras, simplemente deberás separarlos con una coma.

Calculadora de MCD

Para usar la calculadora de máximo común divisor, introduce los números enteros separados por una coma:

Calcular MCD

Pasos para hallar el máximo común divisor

Para sacar el máximo común divisor, básicamente deberemos seguir una serie de pasos bastante similar a la que usamos para calcular el mínimo común múltiplo. A continuación explicaremos el procedimiento, pero primero es necesario definir los elementos que intervienen en este cálculo. Los más importantes son los dos o más valores numéricos a partir de los cuales se calculará el MCD. También debemos conocer los divisores de todos estos números, ya que uno de ellos será el resultado que estamos buscando. Y por último está el divisor común, este es el valor que estamos buscando, el cual te enseñaremos a calcular ahora mismo:

Método de la lista de divisores

• Hacer un listado de todos los divisores: empezaremos escribiendo una lista de todos los divisores de cada número. Idealmente las dibujaremos en horizontal una encima de otra, ya que, de esta manera será más fácil identificar y comparar los divisores. Una vez hayamos acabado de escribir todos los divisores podremos pasar al siguiente punto.
• Identificar todos los divisores comunes: deberemos identificar los divisores comunes (los que se repiten en todas las listas que hayamos escrito). En el caso de estar trabajando solo con dos números, simplemente deberemos fijarnos en dos listas. Pero si tenemos más listas, entonces tendremos que prestar más atención y mirar más números.
• Encontrar el mayor número de entre los divisores: cuando tengamos todos los divisores comunes marcados de alguna manera, solamente nos quedará encontrar el que sea más grande. El cual posiblemente será el valor numérico que se encuentre más hacia la derecha, ya que más a la derecha querrá decir más grande.

En el caso de estar trabajando con números muy grandes, se nos puede hacer bastante lento tener que escribir todos los divisores. Así que te recomendamos usar el siguiente método o incluso, puedes comprobar si alguno de los números con los que estás trabajando divide al resto. Por ejemplo, el MCD de 16, 32 y 64 no podrá ser mayor a 16, entonces simplemente deberás comprobar si el 16 es divisible entre los demás valores.

Método de la descomposición en números primos

• Descomponer cada número en factores primos: lo primero que haremos será descomponer factorialmente todos los números. De esta manera, al descomponer un número en otros más pequeños, veremos qué relaciones numéricas existen entre todos los valores que estamos calculando.
• Juntar todos los factores en una expresión: una vez hayamos descompuesto todos los números, deberemos expresar los factores en una única expresión matemática para cada número. Con lo cual juntaremos todos los factores y nos quedarán todos multiplicados entre sí y si alguno se repite lo expresaremos en formato de potencia.
• Escoger los números comunes con menor exponente: por último deberás encontrar el máximo común divisor a partir de los factores que habrás unido previamente. Para hacer esto elegirás los números comunes y con el menor exponente. Entonces solo quedará resolver esa operación combinada de multiplicaciones y potencias.

Si no te ha quedado muy claro este procedimiento, te recomendamos que mires el vídeo anterior o el ejemplo que encontrarás al final de este artículo.

Vídeo sobre el máximo común divisor (MCD)

¿Para qué se usa el máximo común divisor?

• MCD para reducir fracciones: el MCD nos es muy útil para simplificar fracciones, lo cual es muy común en el ámbito de las matemáticas. Básicamente, consiste en encontrar el máximo común divisor del numerador y del denominador para después dividir ambos por ese número. De esta manera nos queda una fracción equivalente y más sencilla.
• Simplificar cálculos complejos: en muchos casos es muy útil calcular el MCD de dos números para simplificar expresiones matemáticas de alta complejidad. Así puedes seguir resolviendo el cálculo pero de una manera más fácil, porque no tendrás que hacer los cálculos con números tan grandes.

MCD en la calculadora científica

La función del máximo común divisor en la calculadora nos permite determinar el mcd de dos números enteros. Para poder usar esta funcionalidad en una calculadora científica Casio (los modelos más recomendados para estudiantes). Simplemente, pulsaremos la siguiente combinación de teclas ALPHA + MCD. Seguidamente, introducirás el primer número, después pulsarás SHIFT + "," (para introducir una coma) y por último escribirás el segundo valor. Cuando hayas cerrado el paréntesis ya podrás pulsar la tecla igual y así obtener el resultado.

Ejercicios de MCD resueltos paso a paso

A continuación puedes encontrar tres ejercicios de MCD para que practiques, te recomendamos mucho que pruebes de resolver estos ejemplos. Ya que te ayudarán a interiorizar todos los conceptos matemáticos que hemos explicado a lo largo de este artículo. Dicho esto, te dejamos practicar:

Hallar el mcd de 20 y 24

Hallar el mcd de 15 y 30

Calcular el mcd 600 y 1000

Si quieres aprender a calcular el área de una figura geométrica básica, entonces este artículo te será de ayuda. Ya que, a continuación te explicaremos los pasos que debes seguir para calcular áreas con una calculadora o sin ella (por medio de fórmulas). Y no solo esto, también hablaremos sobre la importancia del perímetro en el cálculo de áreas. Por último, comentarte que tenemos una calculadora de metros cuadrados que puede complementar muy bien las herramientas de este artículo.

Calcular área de un cuadrado

Para calcular el área de un cuadrado debemos seguir la fórmula siguiente: Área = a², siendo (a) un lado del cuadrado. Dicho de otro modo, el área de un cuadrado se obtiene a partir del producto de la base por la altura de la figura. Aunque, como los lados de esta figura geométrica son idénticos en cuanto a tamaño, entonces es más fácil hacer el cuadrado de un lado. También podríamos calcular la superficie de un cuadrado usando la fórmula del área del paralelogramo: Área = D² / 2. Pero simplemente recordando la primera te será suficiente.

Calculadora del área de un cuadrado

A continuación puedes encontrar una calculadora del área de un cuadrado online. Su funcionamiento es muy sencillo, simplemente debes introducir el valor de «Lado» y pulsar en calcular, hecho esto se mostrará el resultado en el apartado de «Superficie cuadrado». Ten en cuenta que el resultado estará en metros cuadrados.

Lado: metros



Superficie cuadrado: m²

Calcular el área de un rectángulo

Para calcular el área de un rectángulo debemos seguir la fórmula: Área = base x altura, aunque a veces podemos encontrar variaciones en la escritura de las variables. Por ejemplo, es muy común sustituir «base» y «altura» por las letras «a» y «b», o incluso se suele sustituir la «a» de altura por una «h». Otro uso que tienen estas variables es en el cálculo del perímetro de un rectángulo, en el cual la fórmula es: Perímetro = 2a + 2b. Simplemente hemos hablado del perímetro porque es un concepto que va de la mano con el área.

Calculadora del área de un rectángulo

Esta segunda calculadora te permitirá calcular el área de un rectángulo introduciendo solamente el valor de la base y el de la altura. Una vez hayas introducido los valores de las dos variables y hayas pulsado en «Calcular Área», la calculadora usará la misma fórmula que hemos explicado para poder obtener el resultado.

Base: metros

Altura: metros



Superficie rectángulo: m²

Calcular área de un triángulo

Para calcular el área de un triángulo debemos seguir la fórmula: Área = (base x altura) / 2. Básicamente, es la misma fórmula que la del rectángulo pero partiéndolo entre dos, porque un triángulo es la mitad de un rectángulo. Quizás no lo veas de primeras, pero si analizas la relación entre un triángulo y un rectángulo por medio de la geometría, verás que es verdad lo que acabamos de comentar. De hecho, te recomendamos como ejercicio que intentes juntar el espacio formado por un triángulo equilátero en forma de rectángulo.

Calculadora del área de un triángulo

Esta calculadora te puede ayudar a calcular el área de un triángulo, conociendo solamente su base y su altura. Podemos decir que funciona igual que la anterior calculadora, solo que realiza el cálculo con una fórmula distinta (añadiendo un dos que lo divide todo).

Base: metros

Altura: metros



Superficie triángulo: m²

Calcular área de un círculo

A la hora de calcular el perímetro de un círculo y su área hay mucha confusión entre ambas fórmulas, ya que son muy similares. Entonces, para solventar estas dudas, la fórmula del área del círculo es la siguiente: Área = π x radio² = (1/4) x π x diámetro. Mientras que la expresión para calcular el perímetro del círculo es la siguiente: Perímetro = 2 x π x radio = π x diámetro. Como se puede apreciar hay cuatro variaciones, las cuales se pueden confundir fácilmente entre ellas. Es por eso, que recomendamos pensarlo detenidamente antes de usar alguna de estas fórmulas en un examen.

Calculadora del área de un círculo

Gracias a la ayuda de esta calculadora del área de un círculo podrás calcular el área de cualquier forma geométrica circular que quieras. Y si conoces las medidas del diámetro también puedes hacerlo, ya que el radio es igual al diámetro dividido entre 2. Por último decir que su funcionamiento es muy sencillo, solo debes introducir el valor y seguidamente pulsar en «Calcular Área».

Radio: metros



Superficie círculo: m²

Calcular área de un pentágono

Para calcular el área de un pentágono regular deberás usar alguna de estas dos fórmulas: Área = (5 x Lado x apotema) / 2 = (Perímetro x apotema) / 2. En ambas intervienen el perímetro (es la suma de todos los lados) y la apotema (es la menor distancia entre el centro y cualquiera de sus lados). Por lo cual debes tener claras todas las fórmulas para calcular la apotema, evidentemente lo mismo para el perímetro, pero este es más fácil de calcular.

Calculadora del área de un pentágono

Esta calculadora de la superficie del pentágono regular permite calcular el área de un pentágono por medio de dos métodos: introduciendo la apotema o introduciendo el lado. Porque es posible que en un ejercicio, te hagan calcular el área conociendo solamente el lado o la apotema. Entonces deberás encontrar el valor del contrario, antes de calcular el área del pentágono.

Apotema Lado metros



Superficie pentágono: m²

Calcular área de un hexágono

Para calcular el área de un hexágono regular deberás usar alguna de estas dos fórmulas: Área = (6 x Lado x apotema) / 2 = (Perímetro x apotema) / 2. Como puedes ver no se diferencian mucho de las anteriores fórmulas, simplemente cambia la manera en que calculas el perímetro porque la primera figura tiene cinco lados y la segunda tiene seis lados. En este caso, también te recomendamos que te aprendas las fórmulas relacionadas con la apotema y el cálculo del perímetro. De hecho, hay maneras muy creativas de obtener el valor de los lados, como por ejemplo usando el Teorema de Pitágoras.

Calculadora del área de un hexágono

En esta calculadora de la superficie de un hexágono regular, solamente deberás introducir el valor numérico del lado. Una vez lo hayas hecho, deberás pulsar en «Calcular Área» y obtendrás el resultado inmediatamente. El resultado estará en metros cuadrados, pero siempre puedes convertir esta unidad a otras unidades derivadas.

Lado: metros



Superficie hexágono: m²

Calcular área de un trapecio

Para calcular el área de un trapecio deberás usar esta fórmula: Área = ((Base + base) x altura) / 2, dicho de otra forma deberás hacer la suma de las bases por la altura y dividirlo entre dos. A modo de resumen, para aquellos que no sepan cuál es la forma de un trapecio, tiene un aspecto formado por la suma de un triángulo y de un romboide. Lo cual lo hace complicado de medir en términos matemáticos y geométricos.

Calculadora del área de un trapecio

A continuación puedes encontrar una calculadora del área de un trapecio, la cual funciona a partir de la fórmula que hemos comentado en el apartado de arriba. Simplemente debes tener en mente que la «B» comentada en la expresión matemática de arriba equivale a la base mayor, mientras que la «b» de la fórmula significa la base menor.

Base mayor: metros

Base menor: metros

Altura: metros



Superficie trapecio: m²

Calcular área de un rombo

Para calcular el área de un rombo deberás usar la siguiente fórmula: Área = (D X d) / 2, en ella intervienen dos diagonales que se encuentran en el interior de la figura. Además, existen algunas fórmulas que nos permiten deducir la longitud del lado a partir de las mismas diagonales, lo cual es algo cómodo y muy práctico. Finalmente, mencionar que guarda ciertas similitudes con el paralelogramo en cuanto a forma, lo podrás apreciar si comparas una imagen de cada figura.

Calculadora del área de un rombo

Seguidamente puedes encontrar una calculadora del área de un rombo que funciona a partir de la fórmula matemática que acabamos de comentar en el apartado anterior. Simplemente debes tener en mente que la «D» a la cual nos hemos referido antes simboliza la diagonal mayor y la «d» de la fórmula significa la diagonal menor.

Diagonal Menor: metros

Diagonal Mayor: metros



Superficie rombo: m²

Calcular áreas en la calculadora científica

Si quieres aplicar las fórmulas que hemos explicado a lo largo del artículo en tus clases de matemáticas, lo más recomendable es que compres una calculadora científica propia. Lo bueno es que actualmente existen muchas calculadoras científicas en el mercado, por lo tanto tendrás muchas opciones entre las que elegir. Pero, en lo personal te recomendamos la Casio FX-991SPX para realizar cálculos de áreas, operaciones geométricas y algún cálculo con vectores.

Aprender a calcular los metros cuadrados de un espacio es algo muy útil y, hasta necesario para poder estudiar el temario de geometría de matemáticas. El cual abarca conceptos como superficie, áreas regulares y áreas irregulares. Es por esto que a lo largo de este artículo explicaremos: qué son los metros cuadrados y cómo calcularlos, las equivalencias con otras unidades de superficie y sus aplicaciones. Y también te ofrecemos una calculadora de m² para que resuelvas tus conversiones.

Calculadora de metros cuadrados

A continuación puedes encontrar una calculadora capaz de calcular los m² de un espacio regular. Para poder usarla, simplemente deberás introducir dos valores: el ancho y el largo del espacio y cuando pulses «Calcular», obtendrás el resultado.

Ancho:
metros

Largo:
metros



Metros cuadrados:
m²

¿Cómo calcular metros cuadrados?

Para poder calcular los m² de un espacio deberemos usar una fórmula para sacar metros cuadrados. Pero, dependiendo de la forma de la superficie que queramos cuantificar deberemos usar una expresión matemática u otra, Y es aquí donde deberemos clasificar el espacio en una de las dos siguientes categorías: forma regular o forma irregular. Básicamente, la forma del primer tipo de superficie se puede equiparar a una forma geométrica básica, mientras que la segunda estará formada por más de una figura geométrica. En los siguientes dos apartados acabaremos de definir ambos tipos para que no queden dudas.

Metros cuadrados en una superficie simple

Este caso solo nos permite calcular la superficie de las figuras simples, tales como cuadrados y rectángulos. Entonces, lo que haremos es usar la fórmula del área de esa figura en concreto y obtendremos los metros cuadrados que ocupa ese espacio. Este método es así de fácil. A continuación, puedes ver el ejemplo de un cuadrado que hace 4 metros de largo y 4 metros de ancho. Por lo tanto, si calculamos su área nos da un valor de 4 m x 4 m = 16 m².

Metros cuadrados en una superficie compuesta

Por otro lado, si queremos calcular los metros cuadrados de un espacio que tiene una forma compuesta. Entonces deberemos simplificar el espacio en formas geométricas (cuadrado, rectángulo, triángulo, círculo, pentágono y demás), y después sumar las áreas de todas las figuras. En el siguiente ejemplo puedes ver una figura compuesta por un rectángulo, un triángulo y un cuadrado. Por lo tanto los cálculos quedarían así: 4 m x 4 m = 16 m² (Cuadrado), 4 m x 4 m / 2 = 8 m² (Triángulo) y 8 m x 2 m = 16 m² (Rectángulo). Entonces, la superficie total es 16 m² + 8 m² + 16 m² = 40 m².

Vídeo explicativo sobre los metros cuadrados

Convertir metros cuadrados a otras unidades de superficie

La unidad por defecto de la superficie es el m², pero existen otras unidades del Sistema Internacional. Es por eso que ahora te mostraremos una tabla con las equivalencias en el S.I. y te comentaremos por encima cómo se obtienen. Pero, antes de empezar, debes saber que la superficie es una magnitud derivada de la longitud. Es por eso que ambas comparten el metro, pero la superficie lo usa en dos dimensiones, mientras que la distancia lo usa solamente en una dimensión.

Unidad	Simbología	Equivalencia
kilómetro cuadrado	Km²	1 000 000 m²
Hectómetro cuadrado	hm²	10 000 m²
Decámetro cuadrado	dam²	100 m²
Metro cuadrado	m²	1 m²
Decímetro cuadrado	dm²	0,01 m²
Centímetro cuadrado	cm²	0,0001 m²
Milímetro cuadrado	mm²	0,000001 m²

Estas son las unidades de superficie estándar (basadas en el Sistema Internacional) y tal como se puede ver en la tabla, cada unidad vale 100 más que la anterior. Hay que vigilar con esto, porque al ser m² (no metros) la diferencia entre cada unidad es 10² = 100, y no 10. Además de estas también existen otras medidas de superficie, usadas en algunos países, que no parten del metro, ahora las comentaremos por encima.

Unidades de superficie del sistema inglés

• Yarda cuadrada: equivale a 0,83613 metros cuadrados.
• Milla cuadrada: equivale a 2.589.988 metros cuadrados.
• Pie cuadrado: equivale a 0,092903 metros cuadrados.

Ejercicios de conversión

Ahora que ya has aprendido la teoría para calcular los metros cuadrados de un espacio, simplemente te queda practicar con algunos ejercicios. De esta manera, consolidarás los conocimientos. Dicho esto, te recomendamos que resuelvas los ejemplos que te proporcionamos a continuación y luego compares los resultados con los nuestros:

• 17 m² a dam² = 0,17 dam²
• 156 km² a mm² = 156 000 000 000 000 mm²
• 4263 dam² a yd² (yardas cuadradas) = 509850,56 yd²
• 142 cm² a ft² (pies cuadrados) = 0,15 ft²
• 46 km² + 1845 cm² a m² = 46000000 m² + 0,1845 m² = 46.000.000,1845 m²
• 3 mi² (milla cuadrada) + 374 dam² a km² = 7,77 km² + 0,0374 km² = 7,81 km²

Aplicaciones de los metros cuadrados

A modo de conclusión, queremos explicarte todas las aplicaciones que tienen las medidas de superficie. Ya que al principio del artículo hemos dicho que eran muy útiles, pero no hemos especificado. Entonces, vamos a empezar hablando sobre el tamaño de las habitaciones. Para poder diseñar la distribución de una habitación con todos los muebles, luces, aparatos electrónicos y demás decoraciones, siempre necesitarás calcular los metros cuadrados del suelo. Al menos si quieres sacarle un buen partido a ese espacio determinado, ya que, necesitarás saber la cantidad de superficie disponible.

Por otro lado, los metros cuadrados se usan para calcular los aforos, de hecho es muy probable que alguna vez hayas oído hablar sobre las personas/m² que puede haber dentro de un espacio. Y partiendo de la misma técnica, también se aplica a las plantas. Por ejemplo, el número de plantas por metro cuadrado óptimo para el crecimiento de esa especie en concreto será un valor, mientras que el de otra especie será otro. Y es por eso que todos los agricultores deben conocer estas proporciones. Aunque estas relaciones se suelen expresar con las siguientes unidades de superficie agrarias: hectáreas, áreas o centiáreas.

Esperamos que te haya sido de utilidad este artículo, quizás te interese aprender a calcular metros cúbicos. Si este es el caso, te recomendamos que entres en este último enlace, el cual te llevará a un artículo muy interesante.

Gracias a esta calculadora de fechas podrás calcular el tiempo transcurrido entre dos fechas de una manera fácil y rápida.

Fecha inicial Fecha final

Días transcurridos
Tiempo transcurrido

¿Cómo calcular los días entre dos fechas?

Para poder calcular el total de días transcurridos entre un intervalo de fechas determinado puedes hacerlo mediante dos métodos. El primero es contar los días con la ayuda de un calendario, lo cual es fácil de hacer, pero puede ser bastante cansino si la fecha de inicio es bastante lejana. Por otro lado, puedes usar un método un poco más matemático y hacer la suma de los días que ha habido en cada mes e ir sumando hasta llegar a la fecha final. Este sistema solo tiene la complicación de que debes conocer los días que dura cada mes y que quizás debas tener en cuenta algún año bisiesto.

Si prefieres usar un método más rápido y cómodo, te recomendamos que uses nuestro contador de días y ya verás que no tardarás nada en obtener el resultado que buscas. Incluso podrás realizar cálculos de fechas muy lejanas lo cual seguro que te será de utilidad. Y así podrás resolver cualquier duda que tengas del estilo ¿Cuántos días han pasado desde …?

Nuestro contador de días entre fechas

Nuestro contador de días entre fechas es una herramienta potente y muy exacta, la cual tiene un funcionamiento muy simple. Básicamente, debes insertar dos fechas (la fecha inicial del período y la fecha final), una vez las hayas escrito ya se mostrarán los días transcurridos como resultado. No tienes que hacer nada más y además, siempre podrás reescribir las fechas y por lo tanto, realizar más cálculos.

¿Para qué sirve una calculadora de fechas?

Gracias a esta calculadora de fechas online puedes calcular cuántos días han pasado desde algún día histórico, algún día importante para ti como tu boda, o incluso cuánto tiempo ha pasado desde las últimas vacaciones. Además, esta herramienta también es muy útil para tareas financieras, ya que podrás calcular períodos de inversión e intereses de una manera precisa. Como se puede ver tiene aplicaciones para cualquier ámbito, por eso si crees que necesitarás este recurso más veces en el futuro, te recomendamos que añadas esta página a favoritos.

Calcular la diferencia de fechas en semanas y meses

Esta calculadora de tiempo ofrece el resultado en días, semanas, meses y años. Ya que, de esta manera se ofrecen unos resultados precisos y útiles para distintos tipos de análisis. Esto se debe a que no es lo mismo consultar esta herramienta para contar los días que han pasado desde tu cumpleaños, que consultarla para saber cuántas semanas del embarazo han pasado. Para el primer caso la información se puede ofrecer en cualquier unidad de tiempo (días, semanas y meses). Pero si tenemos en cuenta el segundo ejemplo, la respuesta debe ofrecerse en semanas.

Otras calculadoras de tiempo

A continuación, puedes encontrar un listado de tres calculadoras de tiempo online que pueden serte de ayuda:

• Calculadora de horas, minutos y segundos: este recurso es útil para aquellos casos en que se quiere calcular la diferencia de tiempo entre horas de un mismo día o como máximo un par de días. Es por esto que se suele usar para calcular la última vez que tomaste cierto medicamento o en casos similares.
• Conversor de unidades de tiempo: este es otro recurso muy interesante el cual permite al usuario convertir una unidad de tiempo a cualquier otra. De esta manera, puedes obtener cualquier resultado en una determinada unidad de tiempo, partiendo de otra. Un ejemplo de este tipo de conversores es el conversor de semanas a años, entre muchos otros.

¿Quieres generar un número aleatorio que esté dentro de un rango definido? Entonces, te recomendamos usar nuestro generador de números aleatorios online, ya que, te permitirá conseguir estos números al azar en cuestión de segundos.

Calculadora de números aleatorios

Mínimo:
Máximo:



Número aleatorio resultante :

¿Cómo usar un este generador de números aleatorios online?

Para poder generar un número aleatorio con esta calculadora, primero deberás introducir dos valores (el mínimo y el máximo) y luego pulsar en el botón de «calcular aleatorio». Entonces, automáticamente recibirás un valor en la casilla de «Número aleatorio resultante» y podrás pulsar el botón tantas veces como quieras para repetir el procedimiento. Una última característica que queremos comentar sobre esta calculadora es que genera números aleatorios con repetición. Esto quiere decir que un mismo valor puede salir más de una vez.

¿Cómo generar un número random en la calculadora científica?

Para poder generar números aleatorios en una calculadora científica suele haber la función Rnd (Random). Por lo general, los fabricantes suelen seguir esta pauta de nomenclatura, pero es posible que los modelos de alguna marca funcionen de una manera distinta. Por lo cual, si no encuentras la tecla Rnd en el teclado, deberás buscar alguna opción en el menú que se llame de esta manera o similar. Y si no encontraras ninguna función en los menús, entonces lo mejor es mirar el manual de la calculadora. Así encontrarás la manera correcta de obtener valores numéricos aleatorios, si es que la calculadora lo permite.

Números aleatorios en las calculadoras Casio

En el caso de las calculadoras científicas Casio es muy fácil encontrar la función Rnd, ya que se encuentra en el mismo teclado, sin embargo, existen dos teclas Rnd las cuales tienen funciones distintas:

• RndInt: esta tecla random de la calculadora nos permite generar un número al azar entre dos valores previamente establecidos. La sintaxis de esta función es algo complicada, por eso la escribiremos a continuación: (ALPHA + .) / valor mínimo / , / valor máximo. Por ejemplo, si queremos encontrar un número aleatorio del 1 al 10 nos quedaría algo así: RanInt#(1,10).
• Rnd#: este segundo botón se obtiene de la combinación de teclas (SHIFT + .) y nos permite generar números aleatorios decimales que van desde el 0 hasta el 1.

Mejores calculadoras científicas para generar números aleatorios

Un generador de números random es una herramienta muy interesante, pero, si usas números aleatorios de forma repetida. Quizás sea más cómodo para ti disponer de una calculadora científica económica que incluya la función Random. Por eso, a continuación hablaremos sobre dos modelos que tienen incluida esta funcionalidad y que son muy baratos.

El primero se llama Casio FX-85GTX y es un dispositivo de Casio que ofrece mucha comodidad de uso gracias a su distribución del teclado tan cómoda y gracias a su diseño tan funcional. Además, puedes adquirirla en Amazon por un precio más que decente. El segundo modelo se llama Casio FX-82 Solar II, el cual es un poco más sencillo que el anterior y, por lo tanto, aún más barato. Podemos decir que ambas opciones son muy cómodas de usar y que tienen unos precios muy económicos.

Aplicación de los números aleatorios

Los números aleatorios tienen muchas aplicaciones en el campo matemático de la probabilidad, ya sea para hacer experimentos o simplemente cálculos de probabilidad. En general, la teoría de la probabilidad estudia la frecuencia de ocurrencia de fenómenos aleatorios, por eso los números aleatorios intervienen tanto en esta disciplina matemática.

Por otro lado, si hablamos sobre aplicaciones de la vida cotidiana entonces podemos llegar a pensar en aplicaciones del estilo sorteos y contraseñas. Ya que, el primero requiere de un número ganador que se escoge aleatoriamente y en el segundo ejemplo, los dígitos y su orden son aleatorios.

Métodos para obtener un número random

Actualmente, existen muchos métodos para generar números verdaderamente aleatorios, a continuación las explicaremos en detalle:

• Métodos manuales: lanzar un dado, usar dispositivos mecánicos, lanzar monedas, pedir a una persona que escoja un número aleatorio del 1 al 100…
• Métodos digitales: crear tus propios programas (JavaScript, PHP, Java), usar la función random del Excel, usar una calculadora aleatoria como la nuestra…

Números random en la computación digital

Volviendo a la programación, es bastante común usar números aleatorios en el mundo de la programación. De hecho, se pueden encontrar en el código fuente de muchas aplicaciones, videojuegos, webs y en general, cualquier tipo de programa. Es por eso, que a continuación queremos incluir una guía muy rápida y sencilla de comandos para generar números aleatorios en distintos lenguajes.

• Números aleatorios en PHP: int rand (int $min, int $max)
• Números aleatorios en Python: randint (min, max)
• Números aleatorios en JavaScript: Math.random();

Esperamos que te haya servido de ayuda este artículo y nuestro generador de números aleatorios con intervalos. Si sueles usar este recurso a menudo, te recomendamos que añadas esta página a tu barra de marcadores, de esta manera podrás acceder más fácilmente. Por último, comentarte que si estás interesado en las calculadoras científicas, entonces te será de gran utilidad nuestro artículo sobre calculadoras electrónicas.