Aritmetica

Se conoce como recta numérica a una línea gráfica de dimensión única en la que los números se identifican por medio de puntos marcados que se dividen de manera uniforme.

Dicho de forma simple, se trata de una representación del modo en que se organizan los números reales. Se conoce también como recta real o recta de coordenadas y en ella se encuentran todos los números reales. Se usa con la finalidad de poder ubicar la numeración a través de puntos definidos.

Con frecuencia, esta recta se utiliza como método sencillo de aprendizaje de suma y resta. Sobre todo, en la vinculación de números negativos. Como bien destacamos antes, la recta numérica incluye todos los números reales que continúan infinitamente en cada dirección.

La recta numérica se origina en el número cero. Además, se extiende en ambos sentidos. Por ello, los números de signo positivo se ubican a la derecha y los números de signo negativo hacia la izquierda. Es importante mencionar que, hay una correlación por cada número real y cada punto de la recta. La construcción se realiza de la siguiente forma:

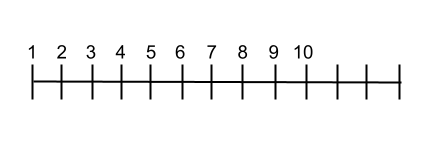
Se escoge arbitrariamente un punto en una línea recta que simbolice el cero o punto inicial. Luego, se selecciona un punto a una distancia correcta hacia el lado derecho del origen para que figure como el número 1. De este modo ya se define la recta real o numérica. A continuación, puedes ver un ejemplo:

¿Cómo se representan los números como puntos en la recta numérica?

Esta es quizás una de las dudas más comunes en los estudiantes de la recta numérica. A decir verdad, la representación de números reales en la recta numérica es muy sencilla. Basta con seguir los siguientes pasos:

1. En primera instancia, se elabora una línea recta horizontalmente. Una vez hecho esto, se define un punto en ella. Dicho punto puede o no estar en el centro. A este punto se le denomina cero.
2. El siguiente paso es seleccionar una medida al azar. Es importante que no sea una medida tan grande a modo que sea posible ubicar varios números. Esta medida es la que se utiliza para definir la posición del número 1 a la derecha con respecto al cero. Esto mismo aplica para el resto de números consecutivamente.

Con relación a lo anterior, es fundamental tener en cuenta la misma medida para separar cada uno de los números.

¿Cómo se ubican los números en la recta numérica?

Como ya explicamos antes, la recta numérica se basa en una línea recta en la que cada punto representa un número. Cuando se trata de números positivos, se admite como número menor al que se encuentra al lado izquierdo del otro. Es decir, el número que más se acerque al cero es menor.

Por otro lado, cuando se quiere definir un número mayor, se toma en consideración el ubicado al lado derecho del otro o que se aleje más del cero. Ahora bien, si los números son negativos, el proceso se realiza de forma opuesta. El número más cercano al cero es mayor y viceversa.

Cuando se quieren ubicar fracciones en la recta numérica, el procedimiento cambia. En este caso, se debe dividir el numerador (número entero) en la cantidad que señala el denominador. Finalmente, se toma la cifra que indique el numerador como resultado de lo primero.

¿Cómo se representan los números decimales en la recta numérica?

Para la representación de números decimales en la recta numérica, lo primero que se debe hacer es posicionar el número que representa la parte entera. Posteriormente, se coloca la parte decimal. En este caso, hay que considerar que cada segmento se divide en 10, 100 o 1000 partes idénticas. Presta atención a este ejemplo:

Si se necesita ubicar el número decimal 0.7 en una recta numérica, hay que cumplir con el siguiente proceso:

1. En primer lugar, comprender que la expresión siete décimos es una extensión en cuya unidad hay 10 décimos. En tal sentido, para encontrarlo en la recta, es necesario hacer una división en diez segmentos iguales.
2. Hay números con signo negativo y positivo. En este caso, 0.7 es positivo. Entonces, debe ubicarse al lado derecho del cero.
3. Para posicionar 0.7 en la recta numérica, se desplaza desde el punto de origen (cero) contando 7 posiciones hacia el sentido derecho.
4. Finalmente, es posible ubicar el punto en que se encuentra 0.7 en la recta numérica.

¿Para qué se utiliza la recta numérica?

La recta real se emplea para representar los números de forma geométrica. Asimismo, todas las operaciones que pueden llevarse a cabo con ellos. Esto pues, como bien sabemos, los números se ubican en la recta organizadamente y con uniformidad.

La recta numérica es relevante cuando se quiere comprender la conversión numérica en diversas operaciones. Adicionalmente, a los números enteros, también es posible representar otros conjuntos numéricos en la recta.

En el espacio entre dos números enteros existe la posibilidad de ubicar infinitos valores decimales. En este caso, aplican tanto números racionales como irracionales. Es decir, es admisible ubicar los números ¼, ¾, ½ entre el espacio desde el 0 hasta el 1.

La utilidad de la recta numérica radica en saber cuándo un número es mayor o menor. Para entender esto, solo es necesario fijarse en la posición del número. Es decir, si está al lado derecho o izquierdo del cero. Así como también, es de gran importancia en la representación de funciones matemáticas de gran complejidad.

Incluso, al definir los ejes cartesianos (x, y, z) para corroborar un cálculo específico, se crean nuevas rectas numéricas. Gracias a estas, es posible realizar la conversión de los resultados de una ecuación en una gráfica para entenderla de una manera más simple.

Algunos ejemplos de operaciones en la recta numérica

En la recta numérica, es posible efectuar distintas operaciones matemáticas. Para entender mejor, usemos algunos ejemplos sencillos.

• Para obtener el resultado de la siguiente operación: -8 + 9 =?

En este caso, hay que posicionarse en “-8” en la recta numérica y moverse 9 lugares en sentido derecho. Después de completar esto, tendremos como resultado = 1. Esta respuesta es el resultado de la adición algebraica expuesta con anterioridad.

• Si por ejemplo, ahora queremos saber cuál es el valor de la operación: 7 – 9=?

Al igual que en el caso anterior, el primer paso es colocarse en el número 7 de la recta numérica. Luego, moverse 9 posiciones. Sin embargo, en este caso, el movimiento es hacia la izquierda, pues se trata de una resta. El resultado es el número negativo -2. De este modo, se resuelve cualquier tipo de operación en la recta real.

Los números decimales son de gran importancia en el mundo matemático, pero ¿sabemos realmente qué son y cómo funcionan? En este artículo lo explicaremos todo.

¿Qué son los números decimales?

Los números decimales son números no enteros (no comprendidos por el conjunto entero), que tienen una parte entera y una parte decimal. Esta parte decimal se escribe detrás de una coma y nos permite expresar valores más pequeños que la unidad.

Los números decimales son una forma de representar números fraccionarios. Esto se debe a que el concepto de fracción es bastante similar al de valor decimal. Podemos verlo, en el siguiente ejemplo: 7/2 es igual a 3,5. Mantienen una equivalencia numérica, solo que se escriben diferente.

El número «3,5» es un número decimal que se lee como «tres coma cinco», su parte entera es el 3 y su parte decimal es igual a 5. Como los números decimales se expresan mediante el sistema de notación decimal, podemos descomponer el número así:

Nomenclatura decimal

En la escritura numérica de estos números, se suelen usar dos tipos de notaciones: la notación estándar (o notación decimal) y la notación científica. Esta primera es la más habitual y es la que hemos estado utilizando hasta ahora.

Mientras que la notación científica se trata de una forma abreviada de la notación estándar. En la notación científica, se escribe un número decimal como un número entero multiplicado por una potencia de 10. Por ejemplo, la cantidad 0,0054 se puede escribir en notación científica como 5,4 · 10^-3.

En cuanto a la escritura no numérica de los decimales, empleamos una notación que se refiere a la posición que ocupa cada dígito decimal. Pues igual que la parte entera tiene: la unidad, la decena, la centena… La parte decimal tiene: la décima, la centésima, la milésima…

Lo que marca el nombre de cada cifra es la posición que tiene respecto a la coma decimal. De esta forma, cuando tienes un número decimal, y quieres saber qué valor tiene la centésima, debes fijarte en la segunda cifra (desde la coma decimal, hacia la derecha). En el anterior caso, la centésima es igual a 5.

Tipos de decimales

Los números decimales se pueden clasificar de la siguiente manera:

• Decimal exacto: tiene un número determinado y finito de decimales. Por ejemplo: el 9,263.
• Decimal periódico: tiene un número infinito de decimales.
  • Decimal periódico puro: la parte decimal está compuesta por un número que se repite de manera infinita. Por ejemplo: el 2,1515151515… Puesto que el 15 se repite indefinidamente.
  • Decimal periódico mixto: la parte decimal está compuesta de un valor, seguido de otro número que se repite de manera infinita. Por ejemplo: el 2,4615151515… Puesto que el 46 no se repite.
• Decimal no periódico: tiene una parte decimal infinita, que no se repite. En este apartado encontramos algunas constantes matemáticas, la raíz cuadrada de dos…

Propiedades de los números decimales

Los números decimales tienen varias propiedades, entre ellas:

• Un decimal no se altera si se añaden ceros a la derecha, por lo tanto, el número 0,25 es equivalente a 0,250 y a 0,2500. Básicamente, porque expresan la misma cantidad.
• Los decimales son equivalentes a las fracciones, por ejemplo, la mitad de la unidad (1/2) se representa con 0,5.
• Si multiplicamos o dividimos un número decimal por potencias de diez, debemos correr la coma decimal: hacia la derecha si estamos multiplicando y hacia la izquierda si estamos dividiendo.

• Se puede simplificar un decimal, esto se hace por medio del redondeo de decimales. Este método consiste en expresar menos cifras decimales, modificando al mínimo el valor del número. Si quieres aprender a usar este sistema de simplificación, te recomendamos que entres en este último enlace.

Representación de los números decimales

El conjunto decimal se puede representar en la recta numérica igual que todos los otros conjuntos.

Partiendo de que los decimales tienen una parte entera y una decimal (más pequeña que la unidad), podemos deducir que los decimales se encuentran representados entre los enteros. Por ejemplo, entre el número 0 y el 1, encontramos infinitos decimales. A continuación, puedes verlo representado en la recta:

Como se puede ver en la imagen, hemos escrito las diez décimas que hay entre el 0 y el 1. Aunque, entre esos dos números hay infinitos decimales, así que se puede llegar a hacer representaciones muy complejas. Y además, esto no solo pasa entre el 0 y el 1, sino que pasa entre todos los números enteros.

Operaciones de los números decimales

Las operaciones de los números decimales son similares a las de los números enteros. La única diferencia es que se deben tener en cuenta las posiciones de los dígitos decimales. Por lo tanto, antes de resolver cualquier operación, debes fijarte bien en que estés operando siempre con las mismas cifras: las décimas con las décimas, las centésimas con las centésimas…

A continuación, vamos a hacer un breve repaso de las cuatro operaciones aritméticas básicas con decimales:

• Suma de decimales:

• Resta de decimales:

• Multiplicación de decimales:

• División de decimales:

Usos y aplicaciones de los números decimales

Los números decimales se usan mucho en la vida diaria y en las matemáticas. Por ejemplo, cuando compras algo en una tienda, necesitas saber el precio de lo que estás comprando, y ese precio estará expresado en números decimales. También, se utilizan para medir las distancias, los pesos y otros aspectos de la vida cotidiana.

En las matemáticas, los números decimales nos permiten expresar cantidades muy pequeñas o muy grandes con facilidad. Y también nos permiten hacer cálculos con mayor precisión. Por ejemplo, si queremos calcular la mitad de 3 unidades podemos dividirlo en dos partes iguales y obtener 1,5 unidades.

Las propidades matemáticas son una gran herramienta para resolver operaciones rápidamente, pues son como pequeños trucos de cálculo. En este artículo, explicaremos en detalle las cuatro propiedades más importantes, y concretaremos en qué operaciones aritméticas pueden usarse. Dicho esto, podemos empezar con la explicación.

Propiedad conmutativa

La propiedad conmutativa es una de las propiedades fundamentales de la adición y la multiplicación. Se trata de la propiedad que establece que el orden en el que se suman o multiplican dos números no altera el resultado. Es decir, a+b=b+a y a·b=b·a.

• Ejemplo de la propiedad conmutativa de la suma:

9 + 5 = 5 + 9 = 14

• Ejemplo de la propiedad conmutativa de la multiplicación:

9 · 5 = 5 · 9 = 45

Propiedad asociativa

La propiedad asociativa de la multiplicación y la suma se refiere a la capacidad de intercambiar el orden de los términos en una operación (con tres o más términos), sin cambiar el resultado. Esto se puede ilustrar de la siguiente manera:

a + (b + c) = (a + b) + c

a · (b · c) = (a · b) · c

Los términos entre paréntesis se pueden intercambiar, y el resultado será el mismo.

• Ejemplo de la propiedad asociativa de la suma:

3 + (9 + 5) = (3 + 9) + 5 = 17

• Ejemplo de la propiedad asociativa de la multiplicación:

3 · (9 · 5) = (3 · 9) · 5 = 135

Propiedad distributiva

La propiedad distributiva es una de las propiedades más importantes que existen, especialmente en el álgebra. Esta propiedad se utiliza para simplificar expresiones y hacer los cálculos más sencillos. La propiedad distributiva se puede aplicar al producto de un número por una suma o resta.

La propiedad distributiva establece que, si tenemos un número y lo multiplicamos por una suma o una diferencia, el resultado será igual a la suma o diferencia de los números individuales multiplicados por el número original.

• Ejemplo de la propiedad distributiva con el producto de una suma:

3 · (9 + 5) = 3 · 9 + 3 · 5 = 42

• Ejemplo de la propiedad distributiva con el producto de una resta:

3 · (9 – 5) = 3 · 9 – 3 · 5 = 12

Propiedad identidad o elemento neutro

La propiedad identidad o elemento neutro se refiere a un elemento que no cambia el valor de una operación. En la suma y la resta, el elemento neutro es el 0 y en la multiplicación es el 1. Por lo tanto, se puede decir que:

a + 0 = a

a – 0 = a

a x 1 = a

• Ejemplo de la propiedad identidad de la suma:

5 + 0 = 5

• Ejemplo de la propiedad identidad de la resta:

5 – 0 = 5

• Ejemplo de la propiedad identidad de la multiplicación:

5 · 1 = 5

Propiedades de la resta

Como has podido ver, todas las propiedades que hemos comentado hasta ahora, son aplicables a la suma y a la multiplicación. Pero, solo el elemento neutro es aplicable a la resta. Aunque en realidad, hay un par más de propiedades de la resta:

• La propiedad fundamental de la resta: la cual dice que: «si sumamos o restamos el mismo número al minuendo y al substraendo, obtenemos una resta equivalente».

A continuación, te lo demostramos con un ejemplo numérico, partiendo de la resta 9 – 5:

9 – 5 = (9 + 1) – (5 + 1) = 4

• La segunda propiedad de la resta: si sumamos el resultado de una resta más el sustraendo, obtenemos el minuendo:

6 – 4 = 2, y se cumple que 4 + 2 = 6.

El conjunto de los números enteros es una colección de todos los números positivos y negativos. En este artículo, te hablaremos sobre las propiedades de estos números, su representación en la recta numérica, las operaciones que puedes hacer con ellos y mucho más.

¿Qué son los números enteros?

Los números enteros son todos los números naturales y negativos, no decimales. Por lo tanto, en matemáticas, el conjunto de los números enteros es el conjunto de todos los números naturales más el conjunto de los números negativos y el número cero. Este conjunto es, a su vez, es una subcategoría del conjunto de los números racionales.

Los números enteros son los números naturales más los negativos. Por lo tanto, los números enteros comprenden el intervalo siguiente: {-∞, …, -3, -2, -1, 0, 1, 2, 3, …, ∞}. En consecuencia, es de vital importancia entender bien el conjunto de los naturales y sus inversos (los negativos), para poder comprender los enteros.

Subconjuntos de los números Z

A partir de lo que hemos explicado hasta ahora, podemos deducir que existen dos tipos de números enteros: los números enteros positivos (naturales) y los números enteros negativos (negativos). A estos dos conjuntos numéricos se les llama subconjuntos de los números enteros.

Aunque, también podemos plantear otros subconjuntos, como los números impares y pares, y los números primos y compuestos. Pues la teoría de conjuntos aplicada a la aritmética nos permite agrupar los números por medio de cualquier propiedad matemática que los describa.

Ejemplos de números enteros

Para dejar un poco más claro qué es un número entero, a continuación te mostramos unos cuantos ejemplos ordenados: 

-8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8.

Como ves son los primeros ocho números positivos (1, 2, 3, 4, 5, 6, 7, 8), el cero y los inversos de los anteriores números naturales. Evidentemente, estos diecisiete ejemplos son solo una parte de todo el conjunto. Pero, a partir de este pequeño grupo de valores, puedes conceptualizar cualquier número entero.

Características del conjunto de números enteros

Este conjunto numérico tiene una serie de características:

• Es infinito, pues está compuesto por dos conjuntos numéricos infinitos (el de los números naturales y el de los negativos).
• Todos los valores de este conjunto tienen signo: positivo (+) o negativo (-), excepto el cero.
• Tienen un orden determinado: los números negativos son menores que cero y, los positivos son mayores que cero: Negativos < 0 < Positivos.
• Todos los números enteros son racionales, pero no son fraccionarios.
• Para cualquier entero positivo existe un entero negativo igual, pero con signo contrario.

Representación de los números enteros

En el anterior apartado hemos comentado por encima del orden de los números enteros. Pero, para verlo aún más claro, te lo vamos a mostrar representado en la recta numérica.

Como se puede ver, esta recta numérica es la combinación de las rectas numéricas de los números naturales y de los negativos. En resumen, los números negativos de mayor valor absoluto son los que van más a la izquierda (más pequeños). Mientras que los números positivos con mayor valor absoluto son los que van más hacia la derecha (más grandes).

Propiedades de los números enteros

Antes de aprender a hacer operaciones con los enteros, es muy importante conocer una serie de propiedades. De esta manera, podremos operar fácilmente y sin equivocarnos.

Te mostramos estas propiedades en esta lista:

• Conmutativa: en las sumas y las multiplicaciones de dos valores enteros, no importa el orden de los factores. Por lo tanto, para todos los números enteros a y b:

a + b  = b + a

a · b = b · a

• Asociativa: en las sumas y las multiplicaciones de tres valores enteros o más, no importa el orden de los factores. Como resultado, para todos los números enteros a, b y c.

a + (b + c) = (a + b) + c

a · (b · c) = (a · b) · c

• Distributiva: la multiplicación de un número por una suma es equivalente a sacar factor común:

a · (b + c) = a · b + a · c

• Elemento neutro: existen dos números que cuando participan en una operación con enteros no modifican el valor inicial. Para la multiplicación es el 1 y para la suma es el 0.

a · 1 = a

a + 0 = a

• Valor absoluto: todo entero negativo tiene un entero positivo idéntico, pero sin el signo. Esto también se aplica a los enteros positivos, pero el valor absoluto de un positivo es el mismo positivo.

|-a| = a

|a| = a

Si quieres aprender en mayor detalle estas propiedades, te recomendamos que te mires nuestro artículo sobre las propiedades matemáticas de las operaciones.

Operaciones con los números enteros

Ahora ya conoces, las características del conjunto Z (entero), cuál es su orden y las propiedades de este conjunto para resolver operaciones. Por lo tanto, ya podemos hablar sobre las operaciones en sí.

• La suma de enteros: si estamos sumando dos enteros del mismo signo, sencillamente sumamos sus valores absolutos y añadimos el signo delante. Mientras que, si estamos sumando un positivo y un negativo, tenemos que restar sus valores absolutos y escribir el signo del entero con mayor valor absoluto:

4 + 5 = 9

(-4) + (-5) = -9

4 + (-5) = -1

• La resta de enteros: cuando restamos dos enteros, debemos aplicar la ley de los signos. Puesto que nos permite simplificar las sustracciones que tienen más de un signo seguido. Y así las convertimos en sumas, que ya sabemos resolver (explicado en el apartado anterior). En la siguiente tabla queda explicada la ley de los signos:

(+) · (+) = (+)

(+) · (-) = (-)

(-) · (+) = (-)

(-) · (-) = (+)

A continuación, te planteamos todos los casos que podemos encontrarnos:

4 – 5 = 4 + (-5) = -1

5 – 4 = 5 + (-4) = 1

(-4) – 5 = (-4) + (-5) = -9

4 – (-5) = 4 + 5 = 9

(-4) – (-5) = (-4) + 5 = 1

(-5) – (-4) = (-5) + 4 = -1

• La multiplicación de enteros: para resolver multiplicaciones de enteros, sencillamente tenemos que multiplicar los valores absolutos. Y después, añadir el signo correspondiente, mediante la ley de los signos, la cual está explicada más arriba. Ahora te mostramos los cuatro casos que existen de multiplicaciones:

4 · 5 = 20

(-4) · 5 = -20

4 · (-5) = -20

(-4) · (-5) = 20

• La división de enteros: por último, tenemos las divisiones, para resolverlas tenemos que hacer el cociente de los valores absolutos y añadir el signo, en función de la ley de los signos. Seguidamente, te mostramos los cuatro casos que puedes encontrarte:

20 ÷ 5 = 4

(-20) ÷ 5 = -4

20 ÷ (-5)  = -4

(-20) ÷ (-5) = 4

¿Cómo se usa el conjunto de los números enteros en la vida diaria?

El conjunto de los números enteros se utiliza en la vida diaria de muchas maneras. Por ejemplo, cuando se trata de medir algo, generalmente se usan números enteros, concretamente enteros positivos.

También se emplean para hacer cálculos matemáticos básicos, como la suma, la resta, la multiplicación y la división. Lo cual se aplica a cualquier acción cotidiana que hacemos, como: comprar, calcular el cambio, medir la distancia de un trayecto, seguimiento del tiempo…

Otras formas en que se pueden utilizar los números enteros en la vida diaria incluyen el ordenamiento de objetos (por ejemplo, colocando libros en un estante por orden alfabético) y el rastreo de ubicaciones (por ejemplo, encontrando un edificio en un mapa). En conclusión, prácticamente cualquier cosa que haces, está rodeada de valores enteros.

En esta lección, aprenderás los números ordinales y los números cardinales en español. Definiremos ambos conceptos, te mostraremos ejemplos de cada uno y te explicaremos cómo se escriben. Además, te enseñaremos dos tablas con los cien primeros números de cada grupo.

Definición de los números ordinales

Los números ordinales se usan para indicar el orden o posición de algo. Por ejemplo, «primero», «segundo», «tercero». Este tipo de números no los utilizamos en operaciones matemáticas. Sin embargo, sí que son muy comunes en prácticamente todos los ámbitos de la vida cotidiana.

Cabe destacar que existen tantos números ordinales como números naturales, puesto que cada valor del conjunto natural tiene su número ordinal asociado.

¿Cómo escribir los números ordinales?

Hay dos modos de escribir números ordinales, la primera forma es mediante los símbolos numéricos. De esta manera, para indicar «primero», debemos escribir 1º. Y así con todos los números: «segundo» se escribe 2º, «quinto» es 5º y así… Y añadimos la terminación -º/-ª.

Estas terminaciones varían según el género del sustantivo al que se refieren (masculino o femenino):

• Masculino: -º: (el primer libro, el segundo día).
• Femenino: -ª: (la primera clase, la segunda opción).

En cambio, si queremos escribir este tipo de números en palabras, se debe emplear una notación específica. La cual se debe memorizar, puesto que no sigue una lógica determinada. Es más bien la suma de diferentes normas y sufijos (no muy bien establecidos), que han resultado de la evolución de la lengua.

Además, también existe otra clasificación según el tipo de número. En primera instancia podemos encontrarnos con los números ordinales simples, los cuales se corresponden a los números que van del 1 al 10. También, se incluyen las decenas (20, 30, etc.): vigésimo, trigésimo… y las centenas (100, 200, etc.): centésimo, ducentésimo…

En segundo lugar, están los números ordinales compuestos, los cuales se forman por la unión de los ordinales simples. Por ejemplo, el 24º se escribe vigésimo cuarto. Lo cual es la suma de vigésimo (20) y cuarto (4).

¿Cuáles son los números ordinales del 1 al 100?

A continuación, te mostramos una lista con los 100 primeros números ordinales. Para que veas más ejemplos de la escritura de estos valores. Y al final de esta lista, te explicamos cómo se escriben los números ordinales mayores de cien.

En cuanto a los números ordinales superiores a cien, hay algunas nomenclaturas que debes conocer:

• 100º se llama centésimo (centésima en femenino).
• 200º se llama ducentésimo (ducentésima en femenino).
• 300º tricentésimo (tricentésima en femenino).
• 400º cuadrigentésimo (cuadrigentésima en femenino).
• 500º quingentésimo (quingentésima en femenino).
• 600º sexcentésimo (sexcentésima en femenino).
• 700º septingentésimo (septingentésima en femenino).
• 800º octingentésimo (octingentésima en femenino).
• 900º noningentésimo (noningentésima en femenino).
• 1000º milésimo (milésima en femenino).

Definición de los números cardinales

Los números cardinales se utilizan para contar. Son los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 y así sucesivamente. Se puede decir que el conjunto de números naturales es equivalente al de los números cardinales.

¿Cómo escribir los números cardinales?

Los números cardinales se usan para contar. Se escriben igual que los naturales. Del uno al diez se llaman de la siguiente manera: uno, dos, tres, cuatro, cinco, seis, siete, ocho, nueve, diez.

Después del diez viene el veinte (20), el treinta (30), el cuarenta (40), el cincuenta (50), el sesenta (60), el setenta (70), el ochenta (80) y el noventa (90). Por último están los cien (100), los 200, 300, 400, 500, 600, 700, 800, 900 y así sucesivamente hasta llegar al billón que es 1.000.000.000.000.

En resumen, se escriben como los números que conoces de toda la vida.

¿Cuáles son los números cardinales del 1 al 100?

Seguidamente, te mostramos los números cardinales del 1 al 100:

Esperamos haberte ayudado a entender los números cardinales y ordinales, y también las diferencias que hay entre ambos. Si quieres preguntarnos algo relacionado con este tema, no dudes en dejarlo en los comentarios.

En este artículo trataremos los números primos y los números compuestos, los cuales son dos conjuntos numéricos contrarios.

¿Cuál es la definición de un número primo?

Los números primos son un conjunto numérico que describe los valores numéricos que solo tienen dos divisores: el número 1 y ellos mismos. Por ejemplo, el 2 es un número primo, ya que solo tiene divisores el 1 y el 2. Sin embargo, el 4 no es un número primo, porque además del 1 y del 4, también tiene como divisor al 2. Entonces, el cuatro es un número compuesto.

Por lo tanto, si intentamos dividir un número primo entre cualquier otro número que no sean el uno y él mismo, no nos saldrá un número natural. Un ejemplo es el número 7, el cual solo se puede dividir en partes iguales entre 1 y 7. Para acabar de entender este concepto, es muy recomendable que pruebes de identificar los números primos comprendidos entre 1 y 10.

Existen ciertos patrones entre los números primos. Por ejemplo, los números primos pares, los números primos impares, los números primos. Y también hay otros tipos de números primos, los cuales los veremos más adelante cuando tratemos algunos teoremas que están relacionados con el conjunto numérico de los primos.

¿Cuáles son los números primos del 1 al 100?

A continuación, te mostramos una lista con los números primos comprendidos entre el 1 y el 100. De esta manera, viendo algunos ejemplos de números primos, acabarás de entender bien el concepto. En especial, te recomendamos que trates de identificar estos números por tu cuenta y después, compruebes si lo has hecho bien con el resultado que te proponemos:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.

¿Qué son los números no primos?

Los números no primos, también conocidos como números compuestos, son aquellos números que no pertenecen al conjunto de los números primos. Si ya sabemos que, un número primo es un número natural mayor que 1 que tiene únicamente dos divisores naturales, a saber, el 1 y él mismo. Entonces, un valor compuesto tiene más de dos divisores.

Por ejemplo, el número 15 es un número no primo, ya que está formado por la multiplicación de números primos (3 x 5). Dicho de otra manera, el número 15 puede dividirse entre 1, 3, 5 y 15, con lo cual no cumple la condición de los números primos.

Los números no primos son importantes en matemáticas y en diversas aplicaciones, como la criptografía. Además, los números no primos juegan un papel crucial en la teoría de números, puesto que se utilizan para demostrar diversos teoremas.

Por ejemplo, el teorema de Fermat se puede demostrar empleando números no primos. Este teorema establece que si un número es divisible por un número primo, entonces ese número también es divisible por todos los números primos que están por debajo de él. Aunque, ya entraremos en mayor detalle sobre este teorema más adelante.

¿Cómo se sabe que un número es primo?

Existen varios métodos para saber si un número pertenece al conjunto de los números primos o no. El más evidente es intentar dividir el valor en cuestión entre todos los valores más pequeños que él. Por ejemplo, si queremos saber si el 5 es un número primo, deberemos dividirlo entre 5, 4, 3, 2 y 1. El resultado nos da que solo se puede dividir entre 5 y 1, así que es un valor primo.

Otro método que podemos emplear es la factorización de números enteros, este es un método para encontrar los factores primos de un número. Así como, el número 21 puede factorizarse como 3 x 7, lo que significa que 3 y 7 son los factores primos del número 15. Y, por lo tanto, el 21 no es un número primo, porque tiene más de dos divisores: 1, 3, 7, 21.

Aunque, también tenemos otro método, algo más elaborado, el cual nos facilita mucho la tarea de identificar un número primo. Seguidamente, lo explicamos:

¿Qué es la criba de eratóstenes?

La criba de Eratóstenes es un método de obtención de números primos. Se llama así en honor a Eratóstenes, quien fue el primero en describirlo. Esta criba es un algoritmo de cribado muy eficiente y sigue siendo el método más utilizado para encontrar números primos.

La criba de Eratóstenes se basa en la idea de que si un número no es primo, entonces es divisible por algún número primo. Por ejemplo, si queremos saber si el número 6 es primo o no, podemos dividirlo por 2 (es un número primo) y 3 (también es un número primo) y vemos que 6 es divisible por ambos.

En general, si un número no es primo, entonces es divisible por algún número primo que esté entre 1 y él mismo. Eratóstenes se basa en esta idea para encontrar números primos.

• Comienza por marcar todos los números como «no primos».
• Luego, marca el número 2 como «primo» y elimina todos los números que sean divisibles por 2 (esto se conoce como «cribar por 2»).

• Luego, marca el número 3 como «primo» y elimina todos los números que sean divisibles por 3.
• Continúa de esta forma hasta que haya marcado todos los números primos hasta el número que se está buscando.
• Al final, todos los números que no hayan sido marcados como «primos» son, de hecho, números primos.

Resulta ser un algoritmo de cribado muy eficiente. Por ejemplo, para encontrar todos los números primos hasta el número 100, solo se necesitan 9 pasos. La criba sigue siendo el método más utilizado para encontrar números primos.

¿Cómo se suman los números primos?

Aunque a primera vista pueda parecer que los números primos no tienen ninguna relación entre sí, de hecho se pueden sumar de forma muy sencilla. Para hacerlo, basta con seguir estos pasos:

1. Escribe los números primos que quieras sumar en una fila.
2. Encuentra el número primo más grande y anótalo en la parte superior de la fila.
3. Encuentra el número primo más pequeño y anótalo en la parte inferior de la fila.
4. Suma los dos números primos y anota el resultado en la parte superior de la fila.
5. Repite los pasos 3 y 4 hasta que solamente te queden dos números primos en la fila.
6. Finalmente, suma los dos últimos números primos y este será el resultado de la suma.

Así de sencillo. ¿Quieres ver un ejemplo? Sumaremos los números primos 5, 7 y 11. Según los pasos que acabamos de ver, el resultado será:

5 + 7 = 12

12 + 11 = 23

Como podemos ver, la suma de los números primos 5, 7 y 11 es 23. ¿Y qué pasa si queremos sumar números primos más grandes? Pues lo mismo, solo que tendremos que seguir los pasos un poco más de cerca. Por ejemplo, sumaremos los números primos 97, 101 y 103. El resultado será:

97 + 101 = 198

198 + 103 = 301

Así pues, la suma de los números primos 97, 101 y 103 es 301. En resumen, sumar números primos es muy sencillo si se siguen los pasos correctamente. ¿Por qué no intentas sumar algunos números primos tú mismo?

¿Cuál es el mayor número primo de dos dígitos?

Este es un buen problema para los matemáticos y para aquellos interesados en los números primos.

Los números primos también son interesantes desde el punto de vista de la teoría de los números. Hay una conjetura, todavía sin resolver, conocida como la conjetura de Goldbach, que dice que todo número par mayor que 2 puede ser escrito como la suma de dos números primos. Así que, ¿cuál es el mayor número primo de dos dígitos?

Aunque no hay una regla fija para determinar el mayor número primo de dos dígitos, se puede utilizar un enfoque similar al utilizado para encontrar el mayor número primo de un dígito. Como sabemos, los números primos de un dígito son 2, 3, 5, 7 y 9. Si utilizamos el mismo enfoque para los números de dos dígitos, podemos determinar los números primos de dos dígitos:

11,13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

¿Quién descubrió los números primos?

Los primeros números primos conocidos fueron descubiertos por los antiguos matemáticos griegos. A Euclides se le atribuye el mérito de ser el primero en demostrar que existen infinitos números primos. Su demostración se sigue enseñando hoy en día en las aulas de matemáticas. Aunque, no fue el único matemático que contribuyó a este descubrimiento.

El gran matemático indio Ramanujan también hizo importantes contribuciones al estudio de los números primos. A principios del siglo XX, desarrolló una nueva forma de encontrar números primos que era mucho más rápida que los métodos que se habían utilizado hasta entonces.

El trabajo de Ramanujan fue fundamental para el desarrollo del ordenador moderno. Sin sus aportaciones, los ordenadores no serían capaces de realizar las tareas que hacen hoy en día. Entonces, ¿quién descubrió exactamente los números primos? Se puede decir que fue un trabajo en equipo de algunas de las mentes más brillantes de la historia.

A continuación, te explicaremos dos teoremas que aportaron muchísimo al estudio de los números primos.

Teorema de Hadamard

Este problema parecía insoluble, pero en 1896, el matemático francés Jacques Hadamard demostró que, en realidad, es posible determinar si un número es primo o no con cierta probabilidad.

El teorema de Hadamard se basa en el análisis de la función matemática que determina si un número es primo o no. Esta función, llamada función primalidad, se puede representar gráficamente como una serie de puntos en una línea. La función o test de primalidad tiene la siguiente forma: P(x) = x/ln(x). Donde x es el número a analizar y ln(x) es el logaritmo natural de x.

La función se puede interpretar como la probabilidad de que un número dado, x, sea primo. Esto quiere decir que, cuando x es muy pequeño, la probabilidad de que sea primo es muy alta, ya que hay muy pocos números en total.

Sin embargo, cuando x es muy grande, la probabilidad de que sea primo es mucho menor. Porque, hay muchos más números y, por lo tanto, es más probable que uno de ellos no sea primo.

La función primalidad también se puede interpretar como la densidad de los números primos en función del tamaño de los números. Esto quiere decir que, cuando x es muy pequeño, la densidad de los números primos es muy alta, ya que hay muy pocos números en total.

Sin embargo, cuando x es muy grande, la densidad de los números primos es mucho menor, ya que hay muchos más números y, por tanto, es más probable que uno de ellos no sea primo.

El teorema de Hadamard establece que, para cualquier valor de x, la función primalidad tiene un valor mínimo en x = 2. Esto quiere decir que, si x es un número primo, entonces la probabilidad de que x sea primo es mayor que la probabilidad de que x + 2 sea primo.

De esta forma, el teorema de Hadamard permite determinar si un número dado es primo o no con cierta probabilidad. Si se analiza un número y se determina que su función primalidad es igual o mayor que la del número siguiente, entonces es más probable que el número analizado sea primo.

¿Qué expresa la teoría de fermat?

El teorema de Fermat afirma que no hay soluciones de números enteros para la ecuación an + bn = cn para n > 2.

Por lo tanto, si se sabe que un número es divisible por un número no primo, se puede deducir que ese número también es divisible por todos los números primos que están por debajo de él. El teorema de Fermat se utiliza en diversas aplicaciones, como la criptografía y la factorización de números enteros.

El teorema lleva el nombre de Pierre de Fermat, que propuso la idea por primera vez en 1637. Afirmó tener una prueba que era demasiado grande para caber en el margen del libro en el que estaba trabajando. La primera prueba completa no fue publicada hasta 1995, por Andrew Wiles.

En 1993, Wiles anunció que había demostrado por fin el último teorema de Fermat, que había desconcertado a los matemáticos durante más de 350 años. La prueba se publicó en 1995 en la revista Annals of Mathematics. Por su logro, Wiles recibió el Premio nobel 2016.

El teorema tiene importantes implicaciones para el estudio de los números enteros. Es un peldaño hacia el concepto más general del último teorema de Fermat, que afirma que no hay soluciones de números enteros distintos de cero para la ecuación an + bn = cn para n > 2.

Conclusión

Esperamos haberte ayudado a entender mejor los números primos. Si tienes cualquier duda respecto a este artículo, no dudes en dejárnosla en los comentarios y trataremos de ayudarte. Y si quieres seguir leyendo sobre las matemáticas y los números, te recomendamos nuestro artículo sobre los conjuntos numéricos.

El número cero es un símbolo importante en muchas culturas y tiene muchos usos en matemáticas y ciencias. En este artículo, vamos a repasar las propiedades del número 0, su utilización, su historia y más. Para cuando hayas terminado de leerlo, conocerás sus aplicaciones matemáticas, sabrás usarlo en el cálculo y conocerás su origen.

¿Qué significa el número 0?

El número cero no siempre fue parte de nuestro sistema numérico. De hecho, el concepto de «cero» es una innovación relativamente reciente. Los primeros sistemas numéricos no tenían una forma de representar el concepto de «nada».

Sin embargo, el desarrollo de la aritmética y la necesidad de expresar cantidades más grandes o pequeñas que las que se podían representar con los símbolos disponibles, hizo que surgiera la necesidad de un símbolo para el cero.

Se emplea simplemente como un símbolo para representar la ausencia de cantidad. Esto lo hace extremadamente útil en el cálculo, ya que nos permite denotar un número que no tiene valor.

Su relación con los demás conjuntos numéricos

El cero se relaciona con otros números de muchas maneras. En primer lugar, se puede pensar en el cero como un número «neutro», porque no afecta el valor de otro número cuando se agrega o se resta. Por ejemplo, 100 es igual a 98 + 2 +0. El cero también es el punto medio de la numeración decimal: 5 está a la derecha del cero y -5 está a su izquierda.

Algo que queremos destacar es que, el número 0 no se incluye en el conjunto de los naturales, aunque algunas veces se incluye dentro por comodidad. Pero, es importante saber que en realidad no forma parte de este conjunto ni del de los negativos, es sencillamente un número entero.

Propiedades del número cero

El cero se puede usar como un operador matemático para denotar la ausencia de valor numérico. Es por eso, que suele denominarse elemento neutro. Además, se representa situado en el centro de la recta numérica, esto se debe a que representa la barrera entre los números negativos y los naturales.

En la lógica matemática, se utiliza para denotar la ausencia, por lo tanto, cuando una proposición lógica es equivalente al cero, se dice que es nulo. Y en la computación, su uso es fundamental, puesto que da sentido al código binario, que es el lenguaje que emplean todas las matemáticas en la programación.

Representación del número cero

Como ya hemos dicho, el número 0 se representa en medio de la recta numérica. Esto se debe a que este valor marca la diferencia entre los números negativos (menores que cero) y los números positivos (mayores que cero). En la siguiente imagen, puedes ver una representación de la recta numérica con el número cero justo en medio:

El número cero en las operaciones matemáticas

El número cero 0 es un valor que representa la ausencia de cantidad. Como tal, es el símbolo empleado en las operaciones matemáticas para indicar que no hay nada que sumar o restar. Aunque pueda parecer un concepto sencillo, el tratamiento del número cero es algo más complejo, en la multiplicación y en la división.

En la suma y en la resta, el 0 es un número que no aporta nada, no hace variar el resultado en nada. Mientras que en las operaciones de multiplicación y división, hace bastante. Por ejemplo, cuando multiplicamos un número cualquiera por cero, el resultado que obtenemos es cero. Da igual cuál sea el número, el resultado siempre será 0.

Por otro lado, si divides el cero entre cualquier número obtienes 0 y si haces la operación al revés, el resultado es infinito. A menos que hagas la operación 0 ÷ 0, que entonces se genera una indeterminación. Como puedes ver, la división con cero es una operación algo más compleja que las anteriores.

La historia del número 0

El número cero se inventó independientemente en diferentes lugares del mundo. Algunos historiadores creen que el primer uso del cero fue en la India, mientras que otros argumentan que fue en Babilonia. Lo que está claro es que el número cero es una invención humana y no tiene un significado inherente.

La invención del cero fue un hito fundamental en el desarrollo de la matemática y tuvo un impacto significativo en la forma en que el mundo es hoy. Sin el cero, los números y las operaciones matemáticas serían muy diferentes, de hecho, no es una exageración decir que el cero da sentido al cálculo moderno.

Algo curioso es que en la antigüedad, los matemáticos griegos no lo utilizaban en sus cálculos. Sin embargo, los mayas sí lo usaban y fue el matemático hindú Brahmagupta quien lo introdujo en Europa en el siglo VII. 
Desde entonces, el cero ha sido muy importante para la humanidad: ha facilitado la tecnología moderna.

Actualmente, el cero tiene una importancia brutal en las matemáticas y ciencia. En física, el cero absoluto es la temperatura más baja posible. En química, el cero de la escala pH representa una solución totalmente ácida. Y en informática, el cero binario es la base de todos los números y cálculos digitales.

Además, el cero también es crucial en la vida diaria. Los números de teléfono y las direcciones postales no serían lo mismo sin el cero. Y por supuesto, sin el cero, los relojes digitales y las calculadoras no podrían existir. ¿Ahora que conoces todo esto sobre el número 0 qué piensas sobre él?